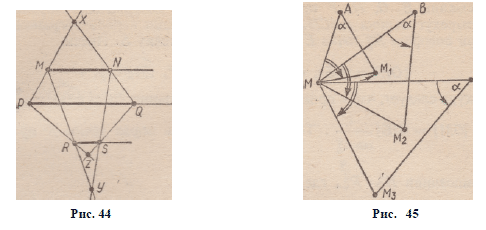Композиция гомотетии
Избранные в опросы теории преобразований подобия плоскости.
Композиция гомотетии. § 6. Общие пары соответственных точек двух преобразований (часть 3).
З. А. Скопец, Л. И. Кузнецова
Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.
Избранные в опросы теории преобразований подобия плоскости.
З. А. Скопец, Л. И. Кузнецова
Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):
Композиция гомотетии. § 6. Общие пары соответственных точек двух преобразований. (часть 2).
Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
3. Если композиция двух гомотетий есть гомотетия, то центры
всех трех гомотетий принадлежат одной прямой.
З а д а ч а 5. Даны три параллельных, попарно не конгруэнтных
отрезка MN, PQ и RS, причем лучи MN, PQ и RS сонаправ-
лены. Доказать, что три точки пересечения пар прямых МР и
NQ, MR и NS, Pi? и QS принадлежат одной прямой; точки пересечения
пар прямых MQ и NP, Qi? & PS, М/? « iVS также принадлежат
одной прямой (рисг 44).
Р е ш е н и е . Обозначим точки пересечения: X = ( М Р ) П ( N Q ) ,
Y ^ ( M R ) П ( N S ) , Z = ( P R ) П (QS).
216 Композиция гомотетии.
Нетрудно заметить, что композиция гомотетий Н{Мх Р) и H { P , z R )
есть гомотетия H { X y R \ Но если композиция двух гомотетий есть
гомотетия, то центры всех трех гомотетий принадлежат одной прямой,
т. е. Y € ( Z X ) .
Аналогично решается и вторая часть задачи.
4. Композиция гомотетии и перемещения есть преобразование
подобия.
З а д а ч а 6. Точка М отображается при поворотах R R ^ t
R% вокруг трех различных центров А, В и С на угол а:
Мг = /tf (М), М2 = R% Щ9 М3 = R% ( М ) .
Доказать, что точки М1У М2, М3 принадлежат одной прямой
тогда и только тогда, когда точки Л, В, С принадлежат одной
прямой.
Р е ш е н и е . Точка Мг есть образ точки М при повороте/?®.
—90°
В то же время — образ точки Л при композиции поворота RM
2 sin-2
и гомотетии Нм , т. е. при преобразовании подобия с центром
М, углом поворота —— 90° и коэффициентом k = 2зт~(рис. 45).
Аналогично и точки М2 и /И3 являются образами точек В и С
соответственно при том же преобразовании. Но образы точек при
подобии принадлежат одной прямой тогда и только тогда, когда
точки принадлежат одной прямой.
З а д а ч а 7. В окружность с центром О вписан четырехугольник
A B C D ] поворот /?g, ср ф 180°, отображает его на четырехугольник
Л1В1С101. Доказать, что пары прямых АВ и АгВ19 ВС
и ВгСъ CD и C x D l y D A и D X A X пересекаются в вершинах параллелограмма.
Р е ш е н и е . Пусть ( А В ) f| (^А) = М, ( В С ) П (^i^i) = N ,
( C D ) П (CiDJ = Р, ( D A ) П 0iЛi) = Q (рис. 46). Ортогональные
217 Композиция гомотетии.
проекции Е , G, Н , F точки О на прямые, содержащие стороны
четырехугольника ABCD, являются вершинами параллелограмма.
При повороте точка Е отображается на точку S. Имеем:
| ОЕ | = | OS |, OEM = OSM = 90°, £OS=cp,
откуда следует, что в прямоугольном треугольнике ЕОМ Е О М — ~
и \ О М | = \ О Е | Тогда точка М есть образ точки Е при
2
ф
композиции Ноk г0> 2Rо» где k
cos:
Аналогично можно показать, что точки N , Р и Q являются
образами точек G , Н и F соответственно при той же композиции,
т. е. при преобразовании подобия. Отсюда следует, что четырехугольник
M N P Q — образ параллелограмма при преобразовании
подобия и, следовательно, также является параллелограммом.
5. Угол между любым лучом и его образом при преобразовании
подобия первого рода — величина постоянная.
З а д а ч а 8. Дан треугольник A B C , С = 90°, [ C D ] — высота.
Доказать, что медианы AM и CN в треугольниках ADC и DBC
перпендикулярны.
Р е ш е н и е . Треугольник CD В отображается на треугольник
ADC при композиции поворота R9£° и гомотетии Hk
D, где k = = | Л С |
СВ |
т. е. при преобразовании подобия первого
рода с углом поворота 90° (рис. 47). При
этом подобии точки С и N отображаются на
точки А и М, а значит, [C7V] — на отрезок
AM. Поэтому отрезки CN и AM перпендикулярны.
З а д а ч а 9 . Даны два одинаково ориентированных
квадрата О А ВС и OAxBxCi.
Найти угол между лучами ААХ и В В Х .
Р е ш е н и е . Луч А А Х отображается
на луч В В Х при композиции поворота
г)45° rrViT ^ ^ о и гомотетии Н о » т. е. при преобра-
зовании подобия первого рода с углом
поворота 45° (рис. 48). А значит, угол между
лучами А А Х и В В Х равен углу поворота
преобразования подобия, т. е. 45°.
218 Композиция гомотетии.