Построение центра преобразования подобия

Избранные в опросы теории преобразований подобия плоскости. §5. Построение центра преобразования подобия.

З. А. Скопец, Л. И. Кузнецова

Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.

Избранные в опросы теории преобразований подобия плоскости.

З. А. Скопец, Л. И. Кузнецова

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

§5. Построение центра преобразования подобия.

Для представления подобия композицией
гомотетии и перемещения так, чтобы
центры гомотетии и поворота совпадали
или чтобы центр гомотетии принадлежал
оси симметрии, необходимо

207 Построение центра преобразований подобия.

уметь строить центр подобия, заданного двумя парами соответственных
точек. Знание способов построения центра, знание его свойств находит
эффективное применение и при решении задач.
Способы построения центра очень разнообразны. Мы рассмотрим
лишь некоторые из них.
1. Принадлежность центра подобия окружности Аполлония.
Пусть преобразование подобия задано двумя парами точек
(Л; Лх) и ( В \ Вх). Если М — центр подобия, то выполняется равенство
\ М А 1 \ ‘ . \ М А \ = \ М В 1 \ : \ M B \ — k , т. е. М принадлежит
множествам точек, отношение расстояний которых до двух данных
точек (Лх и Л, и В ) — величина постоянная. Центр преобразования
подобия есть точка пересечения двух окружностей Аполлония,
построенных для отрезков А Х А и В г В и отношения k . Если
окружности пересекутся (рис. 30), то одна из точек пересечения —•
центр преобразования подобия первого рода, другая — центр
преобразования подобия второго рода. Если окружности касаются
(что возможно тогда и только тогда, когда ( А А г ) || ( В В ^ ) ) , то центры
подобий первого и второго рода совпадают (рис. 31). Если отрезки
А А х и В В 1 параллельны и конгруэнтны, то пары точек (Л; Лх)
и ( В ; В г ) задают перенос и переносную симметрию. Точки, делящие
отрезки ЛХЛ и В Х В в отношении, равном 1, внешним образом, не
существуют. Поэтому не существуют соответствующие окружности
Аполлония, а значит, не существуют и центры (рис. 32).
2. Принадлежность центра преобразования подобия множеству
точек пересечения прямых пучка параллельных со своими образами
при подобии.
При доказательстве существования центра у любого подобия,
отличного от перемещения, было выяснено, что центр принадлежит
прямой, которая является множеством точек пересечения прямых
пучка параллельных со своими образами при преобразовании подобия.
На основании этого свойства центра можно указать два
способа его построения. Один из них уже рассмотрен в процессе
доказательства существования центра. Рассмотрим второй способ.
Пусть а и b — прямые одного пучка параллельных, а с и d —
другого. Прямые а и b пересекаются со своими образами в точках
А и В , a c n d — в точках С и D . Точка S = ( А В ) f) ( C D ) есть центр
преобразования подобия.
Рассмотренное свойство центра дает следующий простой способ
его построения.
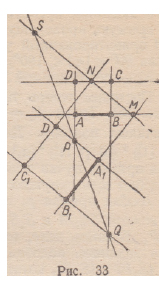
Если преобразование подобия задано парами точек (Л; А х ) и
( В ; В г ) , то строим квадраты ABCD и Л1В1С101 (одинаково или
противоположно ориентированные в зависимости от рода подобия,
центр которого находим). Прямые ЛВ и CD принадлежат одному
пучку параллельных, а прямые AD и ВС — другому. Образы
этих прямых — соответственно (Л^) и (CjDi), (Л^О и { В Х С Х ) .
Если ( А В ) П ( А А ) = М , ( C D ) П (№) = N , ( A D ) П ( А ^ ) = Р ,
( В С ) П (BjCx) = Q, то ( M N ) П ( P Q ) — $ — центр преобразования
подобия (рис. 33).

208 Построение центра преобразований подобия.

Построение центра преобразования подобия

Построение центра в данном случае не
зависит от рода подобия. Оно использует
только аффинные свойства подобий и применимо
для построения неподвижной точки
любого аффинного преобразования.
3. Принадлежность центра преобразования
подобия множеству точек пересечения
прямых центрального пучка со своими
образами.
При отыскании множеств точек пересечения
прямых центрального пучка со своими
образами при подобии используются метрические
свойства преобразований подобия
— угол между любым лучом и его образом
при преобразовании подобия первого
рода — величина постоянная, прямая и ее
образ при подобии второго рода равнонак-
лонены к каждой из двойных прямых. Предварительно
докажем следующие теоремы.
Т е о р е м а 1 . Множество точек пересечения прямых централь-
ного пучка со своими образами при преобразовании подобия первого
рода есть окружность, проходящая через центр пучка, образ центра
пучка и центр подобия.
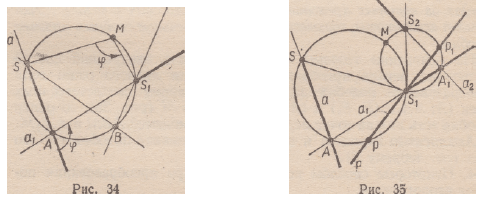
Д о к а з а т е л ь с т в о . Пусть задано преобразование подобия
первого рода, точка М — его центр, ср — угол поворота. Рассмотрим
пучок прямых с центром в точке S, ПмФ (S) = Sx (рис. 34).
Если а — произвольная прямая пучка с центром S, ах — ее образ
при заданном подобии, то (а^а^ = ф, если |ф| ^90°, и (а, аг) =
= 180° — ф, если 90° < | Ф | < 180°. Следовательно, точка А =
= а П % принадлежит окружности SS± М.
Обратно, если точка В принадлежит окружности SSxM, то
sl ((55), ( S . B ) ) =Ф, если | ф | < 9 0 ° , и ((SB), ( S X B ) ) = 180° — ф,
если 90° < |ф| ^ 180° (теорема об измерении вписанных углов).

Построение центра

209 Построение центра преобразований подобия.

Построение центра преобразования подобия второго рода

1) Построение центра преобразования подобия второго рода,
вообще говоря, не является самостоятельной задачей, так как может
быть сведено к построению центра гомотетии. В самом деле,
если 5 — центр преобразования подобия П = Н % ° S a , где S 6 а ,
то имеем:
п2 = (Я* о S a r = Я* о sa о Я* о S a = Я| о 5а о о Я* = Я**.

210 Построение центра преобразований подобия.

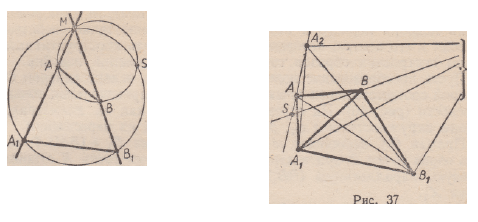
Поэтому для построения центра подобия П, заданного парами точек
(Л; Л,) и ( В ; В х ) , достаточно построить Л 2 = П (Лх) и В2
=П ( B t).
Точка пересечения прямых ЛЛ2 и SS2 искомая (рис. 37).
2) В отличие от преобразования подобия первого рода подобие
второго рода имеет две взаимно перпендикулярные двойные прямые,
пересекающиеся в центре подобия. Поэтому построение центра
может быть сведено к построению двойных прямых.
Пусть преобразование подобия второго рода задано парами
точек (Л; А г ) и ( В ; В г ) . В § 4, п. 10 было отмечено, что одна из
двойных прямых делит отрезок ЛХЛ и [ B X B \ в отношении k внутренним
образом, другая — в отношении k внешним образом. Построив
двойные прямые, найдем точку их пересечения. Она и будет искомой
(рис. 39).
Построение образов точек при преобразовании подобия

Построение образов точек при преобразовании подобия

211 Построение центра преобразований подобия.

В процессе отыскания способов построения центров преобразований
подобия первого и второго рода получены такие свойства
подобия и его центра, которые позволяют указать конструктивный
прием построения образов точек при преобразовании подобия.
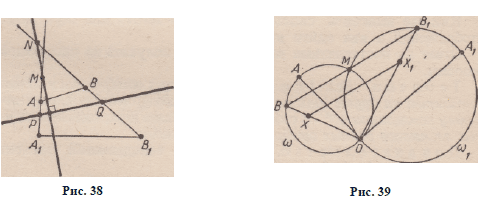
Пусть преобразование подобия первого рода задано центром О
и парой соответственных точек (Л; Лх), а X — произвольная точка
плоскости (рис. 40). На отрезках ОА и О А г , как на диаметрах,
строим окружности со и сolt М — вторая точка их пересечения.
Прямая О Х пересекает ю в точке В . Точка В г £ (В М ) П ®i
есть образ точки В при заданном подобии. Через точку X строим
прямую, параллельную (В В х ). Она пересекает (05х) в искомой
точке Х х .
С преобразованием подобия второго рода связаны пары гипербол.
Если одна пара таких гипербол построена, то построение образов
точек при подобии второго рода выполняется совершенно
аналогично соответствующим построениям для подобий первого
рода.
Свойства подобий в объеме, достаточном для решения широкого
круга задач, рассмотрены. Далее мы остановимся еще на одном
понятии, связанном с преобразованиями, и покажем (позднее),
как оно применяется при решении задач.