Аксиома подвижности

Аксиома подвижности.

Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно: Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ ПЛОСКОСТИ И ЕЕ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. З. А. Скопец, Л. И. Кузнецова

(стр. 227-246)

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

§ 2. Аксиома подвижности.  А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.

Покажем, что в качестве аксиомы подвижности может быть с
равным успехом принято любое из следующих предложений А. IV.I—
A.IV.3.
A.IV.I. Для любых двух пар различных точек Аи Вг и Л2, В2,
таких, что \А1В1\=\ А2В21, существуют хотя бы два перемещения,
отображающих Ах на Л2 и Вг на В2.
Будем говорить, что открытая полуплоскость а’ примыкает к
лучу ОЛ, если прямая ОА является границей этой открытой полуплоскости.
Для краткости объединение луча ОА и примыкающей
к нему открытой полуплоскости а’ будем называть флагом и обозначать
ОАа’. В этих терминах можно сформулировать следующее
допущение.
A. IV.2. Для любой пары флагов 01Л1а[ и 02Л2а’ существует
хотя бы одно перемещение, отображающее один из них на другой.
Чтобы сформулировать следующее возможное допущение, введем
новое понятие.
О п р е д е л е н и е . Осевой симметрией называется перемещение,
множеством неподвижных точек которого является прямая.

250 Аксиома подвижности. 

Прямую, все точки которой при осевой симметрии неподвижны,
называют осью этой симметрии; симметрия с осью р обозначается
■V
A.IV.3. Для любой прямой существует хотя бы одна симметрия,
осью которой является эта прямая.
Во всех указанных формах аксиомы подвижности число перемещений,
обладающих указанными свойствами, оценивается снизу.
Покажем, что на самом деле в каждом из этих трех случаев указано
точное число таких перемещений.
В случае A. IV.1 это уже доказано (см. следствие теоремы 1.3).
Рассуждение, показывающее единственность осевой симметрии,
также основано на применении теоремы 1.3.
Действительно, пусть А и В — произвольные точки прямой р
и С £ а’р. Так как Sp (Л) = Л и Sp (В) = В и, кроме того, симметрия
Sp сохраняет расстояния, то точка Sp (С) должна быть удалена
от Л и В на расстояния а = \АС\ и Ь = \ВС\. Но существует
не более двух таких точек (теорема 1.3), одна из которых — точка
С, а другая (обозначим ее С’) может лежать лишь в открытой полуплоскости
а». Если Sp (С) = С, то неколлинеарные точки А, В
и С — неподвижные точки перемещения Sp и, значит, Sp — тождественное
преобразование (теорема 1.2), что не согласуется с определением
осевой симметрии. Следовательно, Sp (С) = С’. Итак,
образ каждой точки плоскости при осевой симметрии определяется
однозначно, что и означает единственность симметрии с данной
осью.
Отметим, что в ходе доказательства единственности показано:
У.2.1. При симметрии с осью р открытые полуплоскости с границей
р отображаются друг на друга.
Доказательство единственности перемещения, отображающего
данный флаг на другой данный флаг, слегка осложняется тем, что
предварительно требуется показать: при любом перемещении, отображающем
флаг 01Л1а1 на флаг 02Л2а2, точка Ох переходит в 02,
а луч ОлЛх — в луч 02Л2. Это обстоятельство, наглядно очевидное,
нуждается тем не менее в обосновании. Для этого достаточно вспомнить
понятие крайней точки: точка X называется крайней точкой
фигуры Ф, если эта точка не может быть внутренней точкой отрезка,
концы которого принадлежат фигуре Ф.
Легко понять, что единственная крайняя точка флага С^Л^ —
точка Ох. При перемещении F крайние точки произвольного множества
М отображаются на крайние точки множества F (М). (Это
можно доказать рассуждением от противного.) Поэтому при перемещении,
отображающем флаг 01Л1а1 на флаг 02Л2р2, точка Ог
отображается на точку 02. Простое рассуждение, которое читатель
проведет самостоятельно, показывает также, что образом луча
ОхАх при перемещении F может быть только луч 02Л2. Дальнейшее
доказательство единственности искомого перемещения проводится,
как и выше, с помощью теоремы 1.3.

251  Аксиома подвижности. 

Т е о р е м а 2.1. Предложения А.IVЛ — A.IV.3 попарно эквивалентны.
Д о к а з а т е л ь с т в о . Достаточно показать эквивалентность
предложений A.IV.1 и А.IV.2 и привести выводы А. IV.3 из А. IV.2
и A.IV.1 из A.IV.3.
Действительно, в этом случае выводы A. IV.2h3 A. IV.3 и А. IV.3
из A.IV.1 можно провести по схемам A.IV.3 =>A.IV.1 ^A.IV.2
и A.IV.1 =>A.IV.2 =>A.IV.3 соответственно.
1) A.IV.1 фф A.IV.2.
а) Докажем сначала, что А.IV.2 =>A.IV.l. Пусть даны две
пары различных точек Аи Вг и А2, В2, такие, что | AxBt\ = | Л2В2|.
Обозначим открытые полуплоскости с границами АхВг и А2В2
через а[, а» и а’2, а> соответственно. Так как мы предположили
выполнимость A.IV.2, то существуют два перемещения Fx и F2,
отображающие луч АхВх на луч А2В2. Одно из этих перемещений
отображает а[ на а2, другое — на а»2. Поскольку | AxSx| = \А2В2\
и на любом луче имеется только одна точка, удаленная от его начала
на заданное расстояние, то образы точки Вг при этих перемещениях —
точка В2. Так как эти перемещения различны (различны образы
а!), предложение A.IV.1 доказано.
б) Рассмотрим теперь произвольные флаги 01Л1а’1 и 02А2а2.
Отметим на лучах ОгАх и 02А2 такие точки Вг и В2, что | Оа| =
= |02В2|. В силу A.IV.1 существуют два перемещения Fx и F2,
отображающие точки Ог и Вх на 02 и В2 соответственно. Оба эти
перемещения отображают луч ОхАг на луч 02А2, и, следовательно,
остается показать, что одно из них отображает открытую полуплоскость
«1 на а2.
Допустим, что и Fu и F2 отображают а[ на открытую полуплоскость
а2. Возьмем в открытой полуплоскости а\ точку С и
пусть Fx (С) = С’, F2 (С) =я С». Тогда точки Fx (С) и F2 (С) принадлежат
открытой полуплоскости а2 и удалены от точек Л2 и В2 на
расстояния \АС\ и |ВС|. По теореме 1.3 F1(C) — F2(C). Итак,
точки А, В, С не лежат на одной прямой и их образы при перемещениях
Fx и F2 совпадают. Значит, Fx = F2 (теорема 1.2). Но это
противоречит предположению Fx =f= F2.
2) A.IV.2 => A.IV.3.
Рассмотрим на произвольной прямой р луч ОхАх• Перемещение
F, отображающее флаг OlA1
rzP на флаг 01Л1ар, отлично от тождественного
преобразования и переводит все точки прямой р в
себя. Следовательно, это перемещение — симметрия с осью р.
3) A.IV.3 =Ф A.IV.1.
Предварительно докажем следующее предложение.
Л е м м а . Для любых двух точек А и В существует осевая
симметрия, отображающая А на В.
При А —В это утверждение — очевидное следствие A.IV.3.
Пусть Л ф В и М — середина отрезка АВ. Если бы нам удалось

252  Аксиома подвижности. 

дилаза i jd сущеслиивание такии гички iv mt чти |ЛУУ| = | d i \ j,
лемма была бы доказана. В самом деле, ясно, что N ЦАВ) и, значит,
прямая MN пересекает отрезок АВ. Поэтому точки А к В
разделены этой прямой и, поскольку | А VI = |jV5|, \АМ\ — \ВМ\,
из У.2.1 и теоремы 1.3 сразу следует, что Smn (А) = В.
Чтобы доказать существование такой точки N, возьмем произвольную
точку О вне прямой АВ. Если \А0\ = | ОВ|, доказательство
завершено; симметрия с осью АО искомая. Пусть для определенности
\АО\>\ВО\ (рис. 3).
Рассмотрим на отрезке [0, а], где а — | ОА |, функции Д (О —
= | АХ (01 и /2 (0 — | ВХ (01 (X (0 — точка отрезка АО, удаленная
на расстояние t от точки О). Заметим следующие свойства функции
ф (0 = h (0 — /а (*)•
а) Значения <р (0 на концах отрезка [0, а] имеют разные знаки.
Действительно,
ф(0)=/1(0)-М0) = |ЛЛ|-|ЛВ|=-|ЛВ|<0.
Ф (а) = h (a) -/2 (а) = \АО\ -| ОВ| > 0
(по предположению |ЛО|> |ВО|).
б) Функция (р (0 непрерывна на отрезке [0, а].
Свойство б) сразу следует из непрерывности /г (0 и /2 (0 на отрезке
[0, а]. Для доказательства непрерывности этих функций в
каждой точке t0 отрезка [0, а] возьмем произвольное е > 0. При
И — *01 <8 точка X (0 лежит в е — окрестности точки Х0 =
= X (i0) (рис. 3) и в силу известного неравенства (| ЛС| > \\АВ\—
-1ВСЦ)
I h (0 — h (У I = II АХ (t) I -1 AX (t0) к IX (0 X (g I = 11 -101 < 8,
IMO-MOMI5*(o|-|BX(g||<|xx0| = |*-*0Ke,
что означает непрерывность функций (t) и f2 (t) в любой точке
16 [0; а].
Применяя теорему о промежуточном значении, получаем: существует
такая точка t* отрезка [0, а], что ср (t*) = 0, т. е. /х (t*) =
= /2 (/*). Это означает, что существует точка Х*= X (t*) отрезка
ОА, для которой |ЛХ*| = |5Х*|. Лемма доказана.
(В брошюре [1] показана схема построения планиметрии, не требующая
привлечения анализа. Эта схема основана на применении
A.IV.1 в качестве аксиомы.)
Перейдем теперь к доказательству следования
A.IV.3=»A.IV.l.
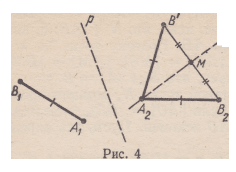
Пусть | Л1В1| = |Л2В2| > 0. С помощью
перемещения F Аулг (тождественного отобра- хо=*\Ч)
жения, если Ах — Л2 или осевой симметрии,
если Лх Ф Л 2, можно отобразить точку Ах на
Л2. Обозначим через В’ образ Вг при этом пе- А
ремещении (рис. 4). Если В’ = Вг, то Faи,— Рис. 3

Аксиома подвижности

253  Аксиома подвижности.

Аксиома подвижности

одно из перемещений, отображаю-
щих Лх на А2 и Вх на В2; второе
такое перемещение — композиция
Sa в1 о Fa а •
ПустьВ’фВг. Имеем: |Л2В’| =
= |Л2В2|. (F а,а — перемещение.)
Поэтому при симметрии FМлг (где
точка М — середина отрезка В’В2
или же точка, равноудаленная от
В’ и В2, если серединой отрезка
В’В2 является Л2) точка Л2 отображается на себя, а В’ — на В2.
И в этом случае существование искомого перемещения доказано.
Другим таким перемещением является композиция Sa2b° Sma,°Fa,a,‘
Доказанная теорема означает, что любое из этих предложений
A.IV.1 — A.IV.3 может быть принято в качестве аксиомы подвижности.
Кроме того, на основании этой теоремы далее мы можем
пользоваться любым из этих утверждений, независимо от того,
какое именно из них принято в качестве аксиомы.

254  Аксиома подвижности.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика.  Математика в школе.

Околоadmin