Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
XI. ДОМИНО
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. XI. ДОМИНО.(стр. 166-167)
Текст для быстрого ознакомления:
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Домино в математике.
132. Все дело в том, чтобы приготовляясь к «угадыванию» и
переворачивая косточки домино «лицом» вниз, тринадцать из них
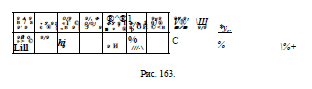
расположить в таком последовательном порядке, как на рис. 163,
Ряд этих косточек, как видим, представляет ряд первых двенадцати
натуральных чисел да еще нуль:
12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0,
и числа эти идут в убывающем порядке. Справа за этим рядом
вы помещаете (тоже «лицом» вниз) еще 12 косточек в каком
угодно порядке. Если теперь вы уйдете в другую комнату, а
кто-нибудь переместит справа налево несколько (менее 12) косточек
и приставит их так, чтобы они шли за (6, 6) влево, то, возвратись,
вы откроете среднюю (т. е. 13-ю по счету, считая слева)
косточку в ряду, и на ней будет как раз столько очков,
сколько было перемещено в ваше отсутствие косточек.
Почему так, нетрудно разобраться. Когда вы уходите в другую
комнату, то вы знаете, что в середине’ ряда перевернутых
166 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Домино в математике.
(0,0). Представим теперь, что перемещена в ваше отсутствие с
правого конца на левый одна косточка. Какая тогда косточка
будет находиться в середине? Очевидно, (0, 1), те. единица.
А если переместить две косточки, то в середине будет находиться
косточка с двумя очками; если переместить три косточки, то в
середине будет косточка с тремя очками и т. д. Словом, средняя
косточка обязательно верно покажет вам число перемещенных
справа на левый конец косточек домино. (Перемещаются, что
надо всегда помнить, не более 12 косточек.)
Игру можно продолжать. Опять уйти в другую комнату и
попросить кого-либо переместить с правого конца на левый еще
несколько косточек. Возвратясь в комнату, вы откроете косточку,
указывающую число перемещенных косточек. Она будет теперь
вправо от средней и, чтобы найти ее, надо за этой средней отсчитать
по порядку ровно столько, сколько косточек было перемещено
в предыдущий раз.
133. Сумма всех очков равна 168. Убедиться в этом можно
непосредственным вычислением, перебрав все 28 косточек домино.
Но это долго и скучно. Поступим иначе.
Предположим, что у нас имеется два комплекта домино.
Разобьем все 56 косточек на 28 пар так, чтобы в каждую пару
входили две косточки из разных комплектов, причем такие что
сумма очков на первых и вторых местах в них равна 6. Напои-
мер: (3, 5) и (3, 1), (6, 4) и (0, 2), (0, 6) и (6, 0), (3, 3) и
(3, 3) и т. д. Это, очевидно, можно сделать. Сумма очков в
каждой паре равна 12, следовательно, сумма очков в двух комплектах
равна 28-12 = 336. В одном же комплекте будет содержаться
вдвое меньше очков, т. е. 168.
Сравните это решение с задачей 38.
136. Предположим, что такой квадрат сложить можно. Проведем
параллельно основанию квадрата три прямые, делящие
боковые стороны квадрата на четыре равные части. По условию
каждая из проведенных прямых пересечет хотя бы одну косточку
домино. Но над любой из прямых лежит четное число (4, 8 или
12) маленьких квадратов, равных
половине косточки. Поэтому каждая
прямая пересекает четное число
косточек и, значит, не меньше двух.
Таким образом,’ проведенные прямые
пересекают не менее шести косточек.
Если теперь аналогичным образом
провести три прямые, параллельные
боковым сторонам, то и они должны
пересечь не менее шести косточек.
Поскольку ни одна косточка не может
пересекаться двумя прямыми, то
в нашем квадрате должны присутствовать
по крайней мере 12 косточек,
что ^невозмо^но.
137. «Такой квадрат сложить нельзя. Показать это можно
точно так же, как и в предыдущей задаче. Необходимо провести
по пяти прямых, параллельных сторонам квадрата.
138. Прямоугольник сложить можно. Одно из решений приведено
на рис. 164.
а
Рис. 164.
167 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Домино в математике.