Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ(стр. 146-153)
Текст для быстрого ознакомления:
Математика школьные знания.
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ
VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ
77. Положите кусок бумаги неправильной форгды на стол и
сделайте сгиб близ края. Пусть полученный при этом сгиб будет
XX’ (рис. 139). Это прямая линия. Проведите ножом по
сгибу и отделите меньшую часть куска. Таким образом вы получите
прямолинейный край. Подобно предыдущему, согните бумагу
по линии DY так, чтобы прямолинейный край XX’ накладывался
аккуратно сам по себе. Развернув затем бумагу, вы убедитесь,
что сгиб DY идет под прямым углом к краю XX’ так как
наложение показывает, что угол YDX’ равен углу YDX. Как
146 Математика школьные знания. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ.
раньше, проведите ножом по второй складке и удалите ненужную
часть.
Повторяя указанный прием, вы получите края СВ и ВА. Наложение
докажет, что углы Л, В, С и D равны друг другу и
прямые и что стороны ВС и CD соответственно равны DA и АВ.
Итак, полученный кусок бумаги ABCD (рис. 139) имеет форму
прямоугольника. Наложение доказывает следующие его свойства:
1) четыре его угла все прямые;
2) четыре же стороны не все равны;
3) но две более длинные стороны равны между собой, а две
более короткие — между собой..
78. Взяв прямоугольный кусок бумаги A’D’CB, складываем
его наискось так, чтобы одна из коротких сторон, например СВ,
легла на длинную В А’, как это показано на рис. 140.
Угол В поместится на‘краю ВА’ в точке Л, конец перегиба
по краю CD’ получится в точке D. Сделаем затем перегиб через
точки Л и D, отогнув по прямой AD часть A’D’DA, которая выдается.
Развернув после этого лист, найдем фигуру ABCD, которая
и есть квадрат. В нем все углы прямые и все стороны
равны.
79. Возьмем квадратный кусок бумаги и сложим его вдвое
так, чтобы противоположные края его совпадали (рис. 141). Получается
сгиб/проходящий через середины двух других сторон
и перпендикулярный к ним. На этой средней линии квадрата берем
какую-нибудь точку и делаем такие сгибы, которые проходят
через эту точку и через углы квадрата, лежащие по обе стороны
средней линии. Таким образом получаем равнобедренный треугольник,
в основании которого лежит сторона квадрата. Средняя
линия делит, очевидно, равнобедренный треугольник на два
совпадающих при наложении и прямоугольных треугольника.
Она же делит угол при вершине равнобедренного треугольника
пополам.
147 Математика школьные знания. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ.
80. Возьмем на средней линии квадрата такую точку, чтобы
расстояния ее от двух вершин квадрата были равны его сторону,
и сделаем сгибы, как выше. В таком случае получим равносторонний
треугольник (рис. 142).
Требуемую точку на средней линии квадрата найти легко.
Для этого надо над АА’ (рис. 142) поворачивать основание АС
около одного из его концов Л, пока другой его конец, С не упадет
на среднюю линию в В.
81. Перегибаем квадрат через середины противоположных
сторон (рис. 143). Получаем линии АОВ и COD. На сгибах АО
и ОБ строим известным нам уже способом равносторонние треугольники
АОЕ, AON, BOF, BOG.
Делаем сгибы EF и NG.
Многоугольник AECFBGDN и будет правильным шестиугольником,
в чем каждый без труда убедится сам. Наибольшее расстояние
между точками многоугольника есть, очевидно, АВ.
82. Возьмем квадрат и известным уже нам способом посредством
сгибов впишем в него другой квадрат (рис. 144). Разделим
пополам углы между сторонами данного и вписанного квадратов.
Пусть сгибы, делящие эти углы пополам, пересекаются
в точках Еу F, G и Н..
148 Математика школьные знания. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ.
Полученный многоугольник AEBFCGDH и есть искомый правильный
восьмиугольник. Действительно, треугольники ABE, BFC,
CGD и DHA в нем равнобедренные и при наложении совпадают.
Значит, стороны полученного восьмиугольника равны.
Углы многоугольника AEBFCGDH тоже равны. В самом
деле, каждый из углов при вершинах Е, F, G, И тех же треугольников
равен полтора раза взятому прямому углу, так как
углы при основании этих треугольников равны четверти прямого
угла. Отсюда ясно, что и углы восьмиугольника при точках А,
В, С и D также равны полтора раза взятому прямому углу
каждый, т. е. все углы восьмиугольника равны между собой.
Сторона взятого квадрата а представляет наибольшее расстояние
между точками восьмиугольника.
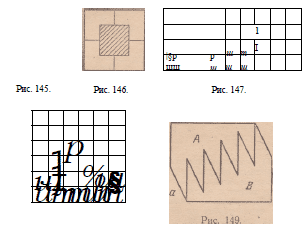
85. При решении этой задачи можно пользоваться листом
картона или бумаги (лучше всего разлинованной на квадратные
клетки). Как сделать требуемую вырезку, видно из рис. 145 и
146. Нетрудно видеть, что все четыре полученные из трех квадратов
фигуры при наложении одной на другую совпадают.
86. Решение задачи видно из рис. 147, 148. Как ни проста и
ни легка эта задача, но она представляет геометрическое толкование
того, что 4 X 9 — 6 X 6. Кроме того, подобного рода задачи
прекрасно подготовляют к более сложным задачам о превращении
одних фигур в другие посредством разрезания их на
части и перекладывания этих частей. Желающий может сам
придумать еще много подобных задач.
87. Решение задачи видно из прилагаемого чертежа
(рис. 149). Если зубчатую часть А вынуть из части В и затем
снова вдвинуть ее между зубьев части В, передвинув на один
зуб вправо, то получится безукоризненный прямоугольник и
даже квадрат.
148 Математика школьные знания. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ.
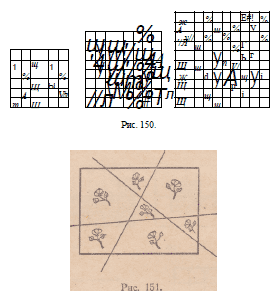
88. Решение задачи приведено на рис. 150.
89. Решение задачи приведено на рис. 151.
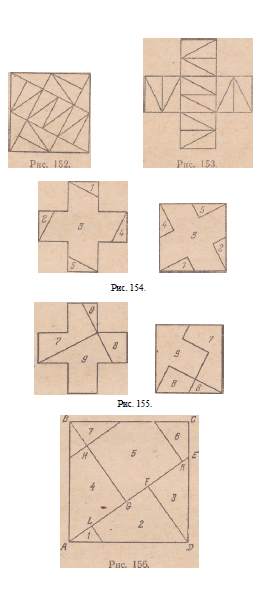
90. 1) Середины сторон квадрата соединим прямыми с противоположными
вершинами квадрата; 2) из середин сторон’квад-
рата проведем линии, параллельные проведенным линиям соединения,
до встреч с другими линиями соединения; 3) в полученных
прямоугольниках проведем диагонали, и тогда данный
квадрат будет разбит на 20 прямоугольных треугольников, как
можно видеть из рис. 152.
Нетрудно показать также, что в полученных прямоугольных
треугольниках катеты таковы, что Один вдвое больше другого.
Из полученных 20 треугольников можно сложить 5 равных
квадратов (рис. 153).
91. На рис. 154, 155 читатель найдет два решения этой задачи.
Второе решение столь же просто, сколь и остроумно: задача
решается проведением всего двух прямых линий.
92. Пусть ABCD (рис. 156)—данный квадрат. Отложим на
его стороне отрезок DE, равный половине диагонали этого квадрата.
Соединим Л с £ и на полученную прямую~Л£ опустим
перпендикуляры DF и ВО. Затем откладываем отрезки GH, GK,
FL, все равные DF\ заканчиваем построение прямыми, параллельными
или перпендикулярными DF, как показано на рис, 156,
150 Математика школьные знания. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ.
151 Математика школьные знания. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ.
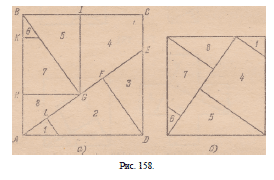
Если разрезать теперь квадрат по проведенным линиям и сложить
затем все полученные части так, как указано на рис. 157,
то получим три искомых квадрата.
* Математическое доказательство зтого\ факта предоставляем
читателю, заметив только, что, пользуясь подобием треугольников
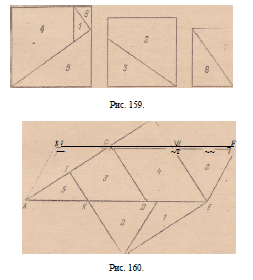
93. Из прилагаемого чертежа (рис. 158) видно, как нужно
разрезать квадрат. Прямые DF и GB и точка L определяются
так же, как и в предыдущей задаче.
Затем параллельно сторонам квадрата проводятся GH и G1
(рис. 158, а) и берется HK—G£I. Таким образом получается
8 частей, из которых и составляются требуемые квадраты. Один
из них представлен на рис. 158,6, .а другой’ есть средний на
рис. 159.
94. Квадрат разрезается точно так же, как в предыдущей
задаче (рис. 158). Из полученных 8 частей составляются 3 требуемых
квадрата так, как на рис. 159.
По данным решениям-рисункам нетрудно доказать математически
правильность этих построений, что желающий вникнуть в
сущность данной задачи пусть и сделает.
95. Разрезаем шестиугольник сначала по диагонали и складываем
полученные 2 половины так, чтобы они образовали па
152 Математика школьные знания. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ.
раллелограмм ABFE (рис. 160). Из точки А, как из центру, радиусом,
равным средней пропорциональной между длиной АЕ и
высотой параллелограмма, проводим окружность, которая пересечет
BF в точке G. Затем из точки Е опускаем перпендикуляр
ЕН на продолжение AG и проводим прямую IK параллельно ЕИ
и на расстояния от нее, равном AG. Таким способом шестиугольник
оказывается разрезанным на 5 таких частей, из которых
можно образовать квадрат. Не разъясняем более этой задачи,
так как предназначаем ее для знающих курс элементарной геометрии
на плоскости.
153 Математика школьные знания. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ.