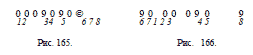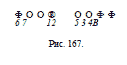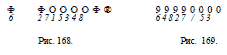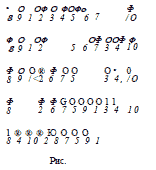Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
XII. ШАШКИ
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. XII. ШАШКИ.(стр. 168-171)
Текст для быстрого ознакомления:
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Шашки в математике.
139. Задача решается в 24 хода следующими перемещениями:
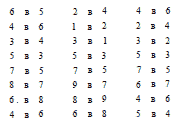
140. Исходное положение шашек показано на рис. 165.
П е р в о е п е р е м е щ е н и е . Слева имеем два свободных
места, перекладываем туда 6-ю и 7-ю шашки. Получается расположение,
как на рис. 166.
В т о р о е п е р е м е щ е н и е . 3-ю и 4-ю шашки перекладываем
на освободившеся места и получаем рис. 167,
Т р е т ь е п е р е м е щ е н и е . 7-ю и 1-ю шашки перекладываем
на свободные места, получаем расположение, как на
рис. 168.
Ч е т в е р т о е п е р е м е щ е н и е . Наконец, перекладываем
на свободные места 4-ю и 8-ю шашки и получаем требуемое
расположение: идут подряд четыре черных и четыре белых шашки
(рис. 169).
Из этого последнего расположения шашек, наоборот, можно
перейти к исходному также четырьмя перемещениями. Решите
эту обратную задачу. Теперь это нетрудно.
168 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Шашки в математике.
141. Первоначальное расположение шашек показано ка
рис. 170. На рис. 171 показаны последовательные перемещения
шашек:
1) перемещаются на свободные
места 8-я и 7-я шашки;
2) перемещаются на свободные
места 3-я и 4-я шашки;
. 3) перемещаются на свободные
места 6-я и 9-я шашки;
4) перемещаются на свободные
места 9-я и 1-я шашки;
5) наконец, перемещаются
на свободные места 4-я и 10^я
шашки.
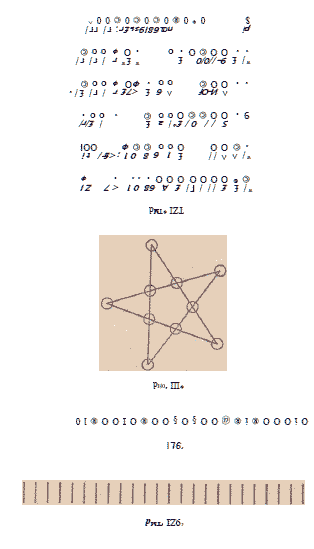
142. Первоначальное расположение показано на рис. 64. По^
следовательные перемещения Доказаны на рис. 172.
143. Первоначальное расположение показано на рис. 65.
Шесть последовательных перемещений показаны на рис. 173. Нетрудно
догадаться, как сделать седьмое и последнее перемещение.
144. Рис. 174 показывает, как решается задача.
145. Для решения задачи шашки нужно поставить так, как
показано на рис. 175.
Как же найти это решение? Поставим в ряд 24 спички
(рис. 176).
169 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Шашки в математике.
170 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Шашки в математике.
Считая от 1 до 7, находим, что в первый раз придется выбросить
7-ю, 14-ю и 21-ю спички. Отбрасываем их и опять начинаем
считать от 1 до 7; сначала отсчитаем три спички за 21-й, а
затем возвращаемся к началу ряда, который содержит теперь
только 21 спичку. Из него придется на этот раз выбросить 4-ю,
12-ю и 20-ю спички. Повторяя этот процесс, на следующем шаге
мы выбросим 5-ю, 15-ю, 24-ю спички, затем 10-ю, 22-ю и, наконец
9-ю спичку. Останется 12 спичек. Если теперь на места оставшихся
спичек поставить черные шашки, а на места выброшенных—
белые, то получим требуемое расположение (рис. 175),
171 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Шашки в математике.