Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.(стр. 162-166)
Текст для быстрого ознакомления:
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Школьные задания по математике.
X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.
118. 1 = У|=55-5.
119. 2 = 1±1.
О
120. 4 = 5 — 4-.
5
121. 5 = 5 + 5 —5 =5 5- 4- .
162 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Школьные задания по математике. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.
122. О = 5 • (5 — 5) = -2^-2- = V5 — 5 = (5 — 5)8.
123. Эта задача сложнее предыдущих. Вот некоторые из ее
решений:
31 = З3 + 3 + 31 =33 -3 +1-, 31 = 33 —
124. 100 = 5- (—2 + 4) ■ (1 + 2 + 7).
125. Чтобы быть победителем, старайтесь только, чтобы вам
удалось назвать число 89. Ясно, что, если вы назовете это число,
то какое бы число (десять или меньше) ни прибавил ваш противник,
вы тотчас найдете соответственное число, добавив» которое
к полученному противником вы получаете сто и выигрываете*
Но, чтобы суметь наверняка сказать «89», а потом, значит, и
«100», постарайтесь разобраться в следующих очень нетрудных
рассуждениях.
Начнем отнимать, сколько возможно, от ста по одиннадцати*
Получим ряд таких чисел: 89, 78, 67, 56, 45, 34, 23, 12, 1. Или
же, если напишем их в порядке возрастания, получим
1, 12, 23, 34, 45, 56, 67, 78, 89.
Запомнить эти числа очень легко: стоит только взять предельное
число, т. е. 10, и прибавить к нему 1 —получится 11 Затем
берем это число и все числа, составленные умножением 11
на 2, на 3, на 4, . . . , на 8, — получим 11, 22, 33, 44, 55, 66, 77,
88; увеличим каждое из этих чисел единицей и начнем единицей
же ряд. Получим опять-таки предыдущий, уже написанный нами
ряд чисел:
1, 12, 23, 34, 45, 56, 67, 78, 89.
Ясно теперь, если вы скажете «1», то какое бы число (по
условию не больше 10) ни назвал другой играющий, он не помешает
вам сказать «12»; точно так же вы всегда можете назвать
23, а затем 34, 45, 56, 67, 78 и 89.
Когда вы скажете «89», то, какое бы число (не большее 10)
ни назвал ваш соперник, вы говорите «сто» и выигрываете.
Отсюда видно также, что если оба играющих знают, в чем
дело, то выигрывает всегда тот, кто первый скажет «один», т. е«
тот, кто начинает игру.
126. Если вы хорошо усвоили решение предыдущей задачи,
то нетрудно видеть, как надо поступать в каждом отдельном
случае.
Пусть, например, назначенное число будет 120; предельное,
как и выше, равно 10. Тогда, очевидно, нужно иметь в виду чис*
да 109, 98, 87, 76, 65, 54, 43, 32, 21, 10, т. е. начиная с 10, все
кратные 11, увеличенные на 10. «Отсюда также видно, что знающий
решение этой задачи выигрывает всегда, если он начинает*
Пусть, например, заданное число будет 100, но предельное
число есть не 10, а 8. В таком случае нужно иметь в виду числа
91, 82, 73, 64, 55, 46, 37, 28, 19, 10, 1, т. е. начиная от единицы,
все числа, кратные 9 и увеличенные на единицу. И в данном
случае знающий задачу всегда выигрывает, если он начинает*
Но если принять за предельное число, например, 9, то числа,
которые нужно иметь в виду, будут 90, 80, 70, 60, 50, 40, 30, 20,
163 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Школьные задания по математике. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.
10. И ясно, что начинающий здесь может проиграть, если другому
известен секрет, ибо, какое бы число начинающий ни сказал,
он не может помешать другому назвать 10, 20 и т. д. — все
числа до 100.
127. Можно перекладывать спички так: 4 к 1, 7 к 3, 5 к 9,
6 к 2, 8 к 10 — или иначе: 7 к 10, 4 к 8, б к 2, 1 к 3 и 5 к 9.
128. Обозначим положенные в ряд спички номерами 1, 2,
3, . . . , 15. Тогда задача решается путем следующих 12 перекладываний:
2 к 6, 1 к б, 8 к 12, 7 к 12, 9 к 5, 10 к 5, 4 между 5
и 6, 3 между 5 и 6, 11 между 5 и 6, 13 на место с номером 11,
14 на то же место, 15 на то же место.
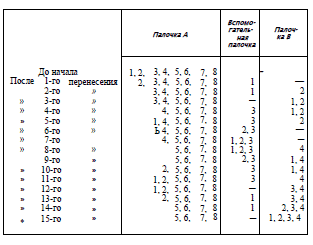
129. Чтобы показать процесс правильного перенесения кружков,
обозначим кружки цифрами 1, 2, 3, . . . , 7, 8, начиная с наименьшего,
затем изобразим процесс перенесения таблицей:
Отсюда мы видим, что на палочку III, когда она свободна,
надеваются только нечетные кружки (1 -й, 3-й, 5-й и пр.), а на
В — только четные. Так что, например, для перенесения четырех
верхних кружков нужно было сначала перенести три верхних на
вспомогательную палочку — что, как видно из таблицы, потребовало
семи отдельных перекладываний, — затем мы перенесли
4-й кружок на третью палочку — еще одно перекладывание — и,
наконец, три верхних кружка со второй палочки перенесли на
ту же третью поверх 4-го кружка (причем 1-я палочка играла
у нас роль вспомогательной), что опять потребовало семи отдельных
перекладываний.
Итак, вообще, чтобы при таких условиях перенести колонну
из п каких-нибудь кружков, расположенных вертикально в убывающем
порядке, нужно сначала перенести колонну из (п—1)
верхних кружков на одно из свободных мест, потом основание,,
164 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Школьные задания по математике. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.
т. е. п-й кружок, на другое свободное место и, наконец, на то же
место опять всю колонну из (п—1) верхних кружков.
Обозначая число необходимых отдельных перенесений буквою
П со значком, соответствующим числу кружков, имеем, следовательно,
П п = 2/7n-i + 1.
Понижая значение п до единицы и делая подстановку, легко
находим
Пп = 2″~‘ + 2″~2 + … + 23 + 22 + 21 + 2°.
Получаем, следовательно, сумму геометрической прогрессии,
которая дает
ПП = 2П- 1.
Таким образом, в случае детской пирамиды из 8 кружков
нужно сделать 28 — 1, или 255, отдельных перекладываний кружков.
Допустим, что перенос одного кружка продолжается всего
одну секунду, тогда на перемещение пирамиды из восьми кружков
потребуется 4 минуты с лишком. Что же касается переноса
башни из 64 кружков, то на это понадобится
18 446 744 073 709 551615 сек.
А это значит, ни более и ни менее, как пять с лишним миллиардов
веков.
130. Ответ на вопрос неожиданно оказывается связанным с
двоичной системой изображения чисел (см. решение задачи 107) *
Представим каждое из чисел 12, 10, 7 в двоичной системе:
12 — 1100
10 — 1010
7 — 111
В каждом столбце получившейся таблицы, за исключением
крайнего правого, стоит по две единицы. Первым ходом игрок А
делает так, чтобы в каждом столбце стояло по две единицы или
ни одной:
12 — 1100
10 — 1010
6 — 110
Своим ходом игрок Б нарушает это свойство, а игрок А его
опять восстанавливает:
1 — 1
7 — 111
6 — 110
Если мы проследим за игрой далее, то увидим, что каждым ответным
ходом игрок А восстанавливает нарушенное предыдущим
ходом Б свойство таблицы содержать в каждом столбце четное
количество единиц.
165 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Школьные задания по математике. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.
Назовем систему из трех целых неотрицательных чисел правильной,
если после представления каждого числа в двоичной
системе любой столбец содержит четное количество единиц, и
неправильной в противном случае.
Легко видеть, что правильная система после любого хода
становится неправильной, а из любой неправильной системы одним
ходом всегда можно сделать правильную. Для этого давайте
выберем самый левый столбец, где стоит нечетное число единиц,
и то из чисел, которое в этом столбце имеет единицу, заменим
на меньшее так, чтобы получилась правильная система. Это, очевидно,
всегда можно сделать.
Если исходная система чисел неправильная (как в нашем
примере), то начинающий игру всегда будет в выигрыше. Для
этого он должен каждым своим ходом делать правильный набор
чисел. Если же исходная система правильная (например, 12, 10,
6 или 13, 11, 6), то ваш противник, если он знает секрет игры,
выиграет у вас, как бы вы ни играли. В этом случае делайте
произвольные ходы в надежде, что противник ошибется и после
его хода система чисел станет неправильной. Тогда перехватывайте
инициативу и доводйте игру до победного конца.
Можно раскладывать спички на 4, 5 и более кучек.
Вы выиграете, если будете играть так, чтобы после каждого
вашего хода в любом столбце таблицы стояло четное число единиц.
166 РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Школьные задания по математике. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.



Отлично!!! Вместо книги на ночь.
Не блог, а поток хороших новостей. Как у вас так получается?
P.S. Сайт, кстати, у вас прикольно сверстан
В каком, кстати, городе живете?
+1. Подписался.
красиво, сделал! Благодарю!!!
Скажите, а у вас есть RSS поток в этом блоге?
И опять об этом. Если поисковики научатся понимать смысл, то блогерам придется поизголяться, чтобы быть читаемыми и не похожими на других.
Читая только ваш блог, я действительно расслабляюсь и получаю удовольствие
И да прибудет с нами сила
Здравствуй! Спасибо за подаренные хорошие эмоции…
Занятно пишете, жизненно. Все-таки, для того, чтобы делать по-настоящему интересный блог, нужно не только сообщать о чем-то, но и делать это в интересной форме:)
Подписался на RSS, буду следить =)
Решил помочь и разослал пост в социальные букмарки. Надеюсь поднимется популярность
Спасибо за статью, всегда рад почитать вас
полностью поддерживаю, такие же мысли были.
Было бы интересно узнать поподробнее
И опять об этом. Если поисковики научатся понимать смысл, то блогерам придется поизголяться, чтобы быть читаемыми и не похожими на других.
При чём тут блогер? Не я же писал эту книгу Школьные задания по математике 🙂
Спасибо за статью, всегда рад почитать вас!
Пожалуйста! 🙂
Сенкс. Интересно, и вообще полезный у Вас блог
как обычно радуешь нас своими лучшими фразами
я бы кое-что добавила, но по сути сказано все
Интересно, я даже и не думала об этом…
Интересные посты — это ваш стиль безусловно!
А что, если завести на сайте-блоге раздел «самые горячие обсуждения» или подобное. Там можно будет обсуждать наиболее горячие топики вашего блога…
Хм… Как раз на эту тему думал, а тут такой пост шикарный, спасибо!
Прикольный пост, на рсску подписался. Будем читать
Только не очень могу понять как часто обновляется ваш блог
Ваш сайт в опере не очень то корректно показывается
Млин, спамеры просто достали уже этим своим примитивом!
Как там у вас с погодой? Давно не писали
Очень понравилось, даже не ожидала.
Спасибо за пост. Позновательно.
не уверена что это так) хотя спасибо
Занятно. Подпишусь-ка я на RSS пожалуй