Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
VI. СКАЗКИ И СТАРИННЫЕ ИСТОРИИ
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.VI. СКАЗКИ И СТАРИННЫЕ ИСТОРИИ(стр. 140-146)
Текст для быстрого ознакомления:
Школьный курс математики.
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ
VI. СКАЗКИ И СТАРИННЫЕ ИСТОРИИ
60. Задача разрешается очень легко, если только решение ее
начать с конца, приняв во вшшание, что после третьего перехода
у крестьянина оказалось ровно 24 коп., которые он должен был
отдать.
В самом деле, если после последнего перехода у крестьянина
оказалось розно 24 коп., то, значит, перед этим переходом у чего
было 12 коп. Но эти 12 коп., получилось после того, как он отдал
24 коп., значит, всего денег у него было 36 коп. Следовательно,
второй переход он начал с 18 коп., а эти 18 коп. получились
у него после того, как он в первый раз перешел мост и отдал
24 коп.. Значит, всего после первого перехода у него было
денег 18 да 24 коп., т. е. 42 коп. Отсюда ясно, что перед тем,—
как первый раз вступить на мост, крестьянин имел в кармане
21 коп. собственных денег.
Прогадал крестьянин! Видно, что на чужой совет всегда
надо еще свой ум иметь.
61. Третий крестьянин оставил для товарищей 8 картофелин,
т. е. каждому по 4 штуки. Значит, и сам он съел 4 картофелины.
После этого легко сообразить, что. второй крестьянин оставил
своим товарищам 12 картофелин, по 6 на каждого, значит, и сам
съел 6 штук. Отсюда следует, что первый крестьянин оставил
товарищам 18 картофелин, по 9 штук на-каждого, значит,-и сам
съел 9 штук.
Итак, хозяйка подала на стол 27 картофелин, и на долю
каждого поэтому приходилось по S картофелин. Но первый крестьянин
всю свою долю съел. Следовательно, _ из восьми оставшихся
картофелин приходится на долю второго 3, а на долю
третьего 5 штук.
62. Задала старинная и многим известная*
140 Школьный курс математики.
Ясно, что овец больше у первого пастуха, у Ивана. Но на
сколько у него больше, чем у Петра?
Если Иван отдаст одну овцу не Петру, а кому-либо другому,
то станет ли у обоих пастухов овец поровну? Нет, потому что
поровну у них было бы только в том случае, если бы эту овцу
получил Петр. Значит, если Иван отдаст одну овцу не Петру, а
третьему лицу, то у него все-таки будет больше овец, чем у Петра,
но на сколько больше? Ясно, что на одну овцу, потому что
если прибавить теперь к стаду Петра одну овцу, то у обоих станет
поровну. Отсюда следует, что пока Иван не отдаст никому
ни одной своей овцы, то у него в стаде на две овцы больше, чем
у Петра.
Теперь примемся за второго пастуха, за Петра. У него, как
мы нашли, на две овцы меньше, чем у Ивана. Значит, если Петр
отдаст, скажем, одну свою овцу не Ивану, а кому-либо иному,
то тогда у Ивана будет на три овцы больше, Чем у Петра. Но
пусть эту овцу получит именно Иван, а не третье лицо. Ясно,
что тогда у него будет на четыре овцы больше, чем осталось
у Петра.
Но задача говорит, что у Ивана в этом случае будет ровно
вдвое больше овец, чем у Петра. Стало быть, четыре и есть
именно то число овец, которое останется у Петра, если он отдаст
одну овцу Ивану, у которого получится восемь овец. А до предполагаемой
отдачи, значит, у Ивана было 7, а у Петра 5 овец.
63. Недоумение крестьянок разрешается очень быстро, если
сообразим, что, сложив свои яблоки вместе и начав их продавать
сообща, они, сами того не замечая, продавали их уже по
другой цене, чем раньше.
Возьмем, для примера, двух последних крестьянок и .рассмотрим,
что они, в сущности, сделали.
Пока первая и вторая думали продавать свои яблоки отдельно,
цена одного яблока у первой была полкопейки, а у второй
— треть копейки. Когда же они сложились и начали продавать
каждые пять яблок по 2 коп., то цена каждого яблока
стала уже 2/5 коп.
Значит, первая крестьянка все свои яблоки продала не по
полкопейки за штуку, а по 2/5 коп. и на каждом яблоке теряла
1/1Л ( 1 2 по 1/10 коп. I — —§ — —[q—5- 4— ~\ 1 V 1 а на всех тридцати яблоках
она потеряла 3 коп. —
Вторая же крестьянка, наоборот, вошедши в компанию, вы-
(2 1 6~5 игрывала на каждом яблоке по 1/15 коп. {-=————————г- — —гр— =
V о д 1о
= а на всех тридцати яблоках выиграла, значит, 2 коп.
Первая потеряла 3 коп., а вторая выиграла только 2 коп*
В общем, все-таки копейка потеряна.
Путем подобных же рассуждений легко узнать, почему у
первых двух крестьянок оказалась «лишняя» копейка.
64. Крестьяне не умели правильно складывать дроби. В самом
деле, сложите все части, на которые крестьяне хотели поделить
находку:
1+1 + 1 + 1 ^ 5 7
3 п 4 5 6 6 0 *
141 Школьный курс математики.
Значит, они все вместе хотели получить меньше, чем нашли (нашли
они 60/60). Найденные деньги вместе с деньгами верхового
были разделены на 60 частей; из них 57/60 отданы крестьянам,
а 3/60, или 1/20, остались у верхового. Но мы знаем, что у верхового
осталось 3 руб. Значит, 1/20 всех денег составляют 3 рубля;
следовательно, всех денег было 3 X 20 =? 60 руб. Карп получил
из этих денег 1/4 часть, т. е. 15 руб.; но, если бы верховой
не приложил своих денег, Карп должен был бы получить на
25 коп. меньше, т. е. 15 руб. — 25 коп. — 14 руб. 75 коп.: такова
1/4 часть найденных денег. Отсюда заключаем, что найдено было
14 руб. 75 коп. X 4 = 59 руб. С деньгами верхового стало
60 руб.; значит, верховой действительно приложил 1 рубль. Приложил
он рубль, а увез 3 рубля: 2 рубля выгадал себе за умный
дележ.
Какие же деньги были найдены в кошельке?
Пять бумажек по 10 руб., одна в 5, одна в 3 и одна в
1 рубль. Сидору верховой дал 20 руб.: две десятирублевки;
Карпу—15 руб.: десятирублевку и пятирублевку; Пахому —
12 руб.: десятирублевку и две рублевки (одну — найденную, другую
— свою); Фоке — последнюю десятирублевку, а трехрублевку
взял себе.
65. Мудрец пустился на уловку. Он прибавил к стаду на
время своего верблюда, тогда их стало 18. Разделив это число,
как сказано в завещании (старший брат получил 18 • — = 9 верблюдов,
средний 18 * = 6 верблюдов, младший 18 • =2 верблюда),
мудрец взял своего верблюда обратно (9 + 6 + 2 + 1 =
= 18). Секрет, как и в предыдущей задаче, заключается в том,
что части, на которые по завещанию должны были делить стадо
сыновья, в сумме не составляют 1. Действительно, -^+ + -g = —
= —
18*
66. Если вода в бочке налита ровно до половины, то, наклонив
бочку так, чтобы уровень воды пришелся как раз у края
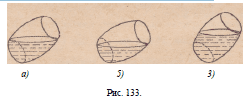
бочки, мы увидим, что высшая точка дна находится также на
уровне воды (рис. 133, а). Это случится потому, что плоскость,
проведенная через диаметрально противоположные точки верхнгй.
и нижней окружности бочки, делит ее на две равные части. Если
вода налита менее чем до половины, то при таком же наклонении
бочки из воды должна выступить часть дна (рис. 133,6),
142 Школьный курс математики.
Наконец, если воды в бочке более половины, то при наклонении
дно окажется под водой (рис. 133, в).
Рассудив именно так, работник справился с заданием*
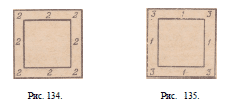
67. Решения приведены на рис. 134 и рис. 135.
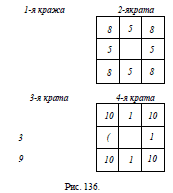
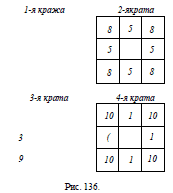
68. Слуга брал себе по бутылке из каждого среднего отделения
и из тех же отделений, чтобы обмануть хозяина, после
каждого воровства прибавлял по бутылке в угловые отделения.;
Так он воровал 4 раза по 4 бутылки, а всего значит, унес 16 бутылок.
Все это видно из рис. 136. Слуга мог расставлять бутылки
и другими способами. Но всегда в первом и третьем столбцах
квадрата он должен был бы оставлять по 21 бутылке и потому
не мог бы унести более 60 — 2-21 = 18 бутылок, т. е. совершить
более четырех краж.
69. В первом случае в пещере остался 21 человек. Рассадить
их с соблюдением условия, чтобы вдоль каждой стены находилось
9 человек, можно многими способами. Один из них показан
на рис. 137.
Во втором случае требуется рассадить 27 человек. Одно из .
возможных решений представлено на рис. 138.
70. Нетрудно видеть, что третьему внуку дед дал грибов
меньше всего, потому что третий внук должен был набрать еще
143 Школьный курс математики.
столько же грибов, чтобы сравняться с братьями. Для простоты
скажем, что третьему внуку дед дал грибов одну горсть.
Сколько же он дал таких же горстей четвертому?
Третий внук принес домой 2 горсти, потому что сам еще нашел
столько же грибов, сколько дал ему дед. Четвертый внук
принес домой ровно столько же грибов, сколько и третий, т’. е.
тоже 2 горсти; но он половину своих грибов растерял по. дороге,
значит, дед дал ему 4 горсти.
Первый внук принес домой 2 горсти, но из них 2 гриба он
сам нашел, значит, ему дед дал 2 горсти без двух грибов. Второй
внук принес домой 2 горсти, да по дороге он потерял 2 гриба;
значит, дед ему дал 2 горсти да еще два гриба.
Итак, дед роздал внукам 1 горсть, да 4 горсти, да 2 горсти
без двух грибов, да 2 горсти с двумя грибами, итого 9 полных
горстей (в двух горстях не хватало по два гриба, зато в двух
других горстях было по два лишних гриба). В 9 равных горстях
было 45 грибов; значит, в каждой горсти 45 : 9 == 5 грибоз.
Третьему внуку дед дал 1 горсть, т. е. 5 грибов; четвертому—
4 горсти, т. е. 5X4 = 20 грибов; первому — 2 горсти без
двух грибов, т. е. ( 5 X 2 ) — 2 = 8 грибов; второму — 2 горсти с
двумя грибами, т. е. (5 X 2) + 2 = 12 грибов.
71. Задача, очевидно, сводится к нахождению такого числа,
которое делится нацело (г. е. без остатка) на 7, а при делении
на 2, 3, 4, 5 и 6 дает в остатке 1.
Наименьшее число, которое делится без остатка на число 2,
3, 4, 5 и 6 (наименьшее кратное этих чисел), есть 60. Нужно,
значит, найти такое число, которое делилось бы на 7 нацело и
было бы вместе с тем на одну единицу больше числа, делящегося
на 60. Такое число можно найти путем последовательных
попыток: 60, деленное на 7, дает в остатке 4, следовательно,
2 X 6 0 дает в остатке единицу ( 2 X 4 = 8 ; 8 — 7 = 1 ) . Значит,
2 X 60 = числу, кратному 7 + 1 ,
откуда следует, что
(7 X 60 — 2 X 60) + 1 = числу, кратному 7,
т. е.
5 X 60 + 1 = числу, кратному 7,
5X 60+ 1 = 301.
Итак, наименьшее число, решающее задачу, есть 301. То
есть наименьшее число яиц, которое могло быть в корзине у женщины,
есть 3014
144 Школьный курс математики.
72. Вопрос, очевидно, сводится к тому, чтобы знать точное
время при возвращении домой. Петр рассуждал так. Я зазол^у
свои часы и перед уходом замечаю их показание, которое, скажем,
равно а. Приходя к знакомому, немедленно справляюсь
у него о времени, и пусть его часы показывают Ь. Перед уходом
от знакомого опять замечаю время по его часам, которые на этот
раз показывают с. Придя домой, я немедленно замечаю, что мои
часы показывают d. По этим данным легко определить искомое
показание часов. Разность cl — а покажет время моего отсутствия
дома. Разность с — b — время, проведенное мною у знакомого.
.Разность (d — а) — (с — 6), полученная от вычитания второго
времени из первого, даст время, проведенное мною в -дороге*
г-, Ъ -{- d — а — с
Половина этого времени ———————————— употреблена мною на
обратную дорогу. Прибавим эту «половину к с, получим
b с d — ti
———————-. это и будет точное показание часов при моем
возвращении домой.
73. По условию вся вырученная сумма, очевидно, не превышает
9997 руб. 28 коп. Значит, число проданных кусков не более
999 728 : 4936, т. е. не более. 202 кусков.
Последняя цифра неизвестного числа кусков должна быть
такова, чтобы она, будучи умножена на 6, давала произведение,
оканчивающееся на 8; такая цифра может быть 3 или 8.
Положим, что последняя цифра неизвестного числа кусков
равна 3. Стоимость трех кусков равна 14 808 коп. Вычитая это
число из вырученной суммы, мы должны получить число, оканчивающееся
на 920.
Если предположить, что последняя цифра равна 3, то вторая
от конца цифра может быть или 2, или 7, так как только эти
цифры, будучи умножены на 6, дают произведения, оканчивающиеся
на 2.
Положим, что неизвестное число оканчивается на 23. Вычитая
стоимость 23 кусков из всей вырученной суммы, получим
число, оканчивающееся на 200. Третья цифра может быть или 2,
или 7; но так как неизвестное число не превосходит 202, то наше
предположение неверно.
Если бы мы предположили, что неизвестное число оканчивается
на 73, то третья цифра была бы равна 4 или 9; такое
предположение тоже неверно.
Итак, последняя цифра не может быть 3; остается предположить,
что она равна 8. Рассуждения, подобные предыдущим,
покажут нам, что вторая цифра может быть или 4, или 9; из
этих двух предположений верным может быть только второе.
Задача имеет одно решение: число проданных кусков разно
98, вся вырученная сумма равна 4837 руб. 28 коп.
74. Надо начинать счет с 6-го солдата, сидящего по левую
руку от хозяина. Во втором же случае — с 5-го из солдат направо
от хозяина.
75. В пылу спора кучер не смог представить, сколь велико
количество запряжек, которые он должен сделать. Подсчитаем
же мы это количество.
Обозначив лошадей цифрами 1, 2, 3, 4, 5 мы должны выяснить,
сколькими способами можно переставить эти пять цифр.
145 Школьный курс математики.
Две цифры можно переставить двумя способами: (1, 2) и
(2, 1). Перестановок из трех 1, 2, 3, начинающихся с цифры 1,
будет также две. Но это число не зависит от того, какая фиксированная
цифра из трех стоит на первом месте. Значит, всего
перестановок из трех цифр будет 3*2 = 6:
Продолжая далее, мы находим, что перестановок из четырех
цифр с фиксированной5первой цифрой будет 6 и множество всех
перестановок из 4 цифр распадается на 4 группы по б переста-
новок, начинающихся с одной и той же цифры—1, 2, 3 или 4.
Так что всех перестановок будет 4-6 = 4-3*2-1 = 24. Аналогично,
множество всех перестановок из 5 цифр состоит из 5 групп
по 24 перестановки, начинающихся с одной цифры—1, 2, 3, 4
или 5. Всего их будет 5-24 = 5-4*3-2-1 = 120.
Можно доказать, что множество перестановок из п цифр
{1, 2, 3, . . . , п} равняется произведению 1 — 2 — 3 . . . п. Это число
обозначается п\
Вернемся к нашей задаче. Итак, кучеру предстояло сделать
120 перепряжек. Если он на каждую затратит только минуту
времени, то на все ему понадобится 2 часа. Кучер проспорил.
76. Если один из мужчин купил, скажем, х предметов, то по
условию он заплатил за них х2 копеек. Если его жена купила
у предметов, то она заплатила за них у2 копеек. Значит, имеем
х2 — у2 = 48, или (х — у) • (х + у) = 48.
Числа xf у по условию целые и положительные. Это возможно
только в том случае, когда х — у и х + у четны и х + у >
> х — у. Разлагая 48 на сомножители, видим, что имеется только
три удовлетворяющие этому условию возможности:
48 = 2-24 = 4-12 = 6-8, или
1*1 — 01 = 2, f *2 ~ у2 = 4, (
1 *1 + У\ = 24, X *2 + У2 = 12, \
Решая эти системы уравнений, находим Xi — 13, уi = 11, Хг = 8,
У2 = 4, х3 = 7, у3 = 1.
Отыскивая те значения х и у, разность которых равна 9,
находим, что Иван купил 13 предметов, Екатерина — 4 предмета.
Точно так же Петр купил 8 предметов, Мария — 1 предмет. Таким
образом, имеем следующие пары:
146 Школьный курс математики.