Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ (часть 2).
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Для младших классов (часть 2). (стр. 43-47)
Текст для быстрого ознакомления:
VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ
82. Правильный восьмиугольник
Как в „данном квадрате построить правильный
восьмиугольник?
83. Оригинальное доказательство
Каждый, изучавший геометрию, знает, что сумма
углов треугольника равна двум прямым углам. Но
мало кому известно, что эта фундаментальная теорема
может быть «доказана» с помощью простого лоскутка
бумаги.
Мы ставим слово «доказана» в кавычки, потому
что это не доказательство в строгом смысле слова, а
скорее лишь наглядная демонстрация. Но все же
этот остроумный прием очень любопытен и поучителен.
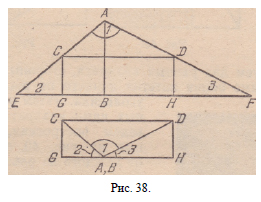
Вырезают из бумаги треугольник любой формы и
перегибают его сначала по линии АВ (рис. 38) так*
задачу — объяснить, почему такое сгибание бумажного
треугольника всегда дает желаемый результат.
Объяснить это нетрудно, и мы не-хотели бы лишить
читателя удовольствия самому подыскать геометрическое
обоснование этого своеобразного «доказательства
».
84. Теорема Пифагора
Показать, что площадь квадрата, построенного на
гипотенузе прямоугольного треугольника, равна сумме
площадей квадратов, построенных на катетах.
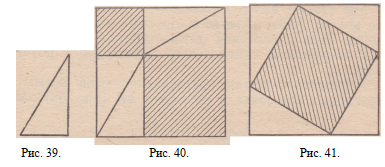
Нарисуем два равных квадрата, стороны которых
равны сумме обоих катетов данного на рис. 39 треугольника.
Затем в полученных нами квадратах произведем
построения, указанные на рис. 40, 41. Здесь
от каждого из равных квадратов мы отнимаем по 4
равных треугольника. Если отнимать от равных величин
поровну, то и остатки) получатся равные. Эти остатки
на рис. 40, 41 заштрихованы; но на рис. 40 получаются
два квадрата, Рис. 42. построенные на катетах
данного треугольника, а на рис. 41 — квадрат, построенный на гипотенузе, и
сумма площадей первых двух квадратов равна, следовательно,
площади второго.
Мы доказали, таким образом, знаменитую теорему Пифагора.
44 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов.
Другое доказательство той же теоремы найдем,
если на взятом бумажном квадрате сделаем сгибы,
как указано на рис. 42. Здесь GEH есть прямоугольный
треугольник и площадь квадрата, построенного
на ЕН, равна сумме площадей квадратов, построенных
на £G и GH.
Призовем теперь на помощь ножницы и будем
не только перегибать, но и разрезать бумагу. Так мы
придем ко многим интересным и поучительным задачам.
85. Как вырезать?
Пусть фигура состоит из трех равных квадратов,
расположенных так, как показано на рис. 43. Вырезать
из этой фигуры такую часть, чтобы, приложив
ее к оставшейся части, получить квадрат, внутри которого
имеется квадратное отверстие.
86. Из прямоугольника — квадрат
Кусок бумаги или картона имеет форму прямо- .
угольника, одна сторона которого равна 4, а другая
9 единицам длины. Разрезать этот прямоугольник
на две равные части так,, чтобы, сложив их надлежащим
образом, получить квадрат.
87. Коврик
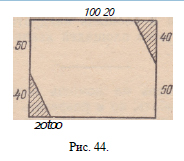
У одной хозяйки был прямоугольный коврик размером
120X 90 сантиметров. Два противоположных
угла его истрепались, пришлось их отрезать (на
рис. 44 эти треугольные куски заштрихованы). Но
хозяйке все же хотелось иметь коврик в форме пря
45 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ
—
моугольника. Онр поручила мастеру разрезать его на
такие две части, чтобы из них можно было сшить
прямоугольник, не теряя, конечно, ни кусочка материи.
Мастер исполнил желание хозяйки.
Как ему удалось это сделать?
88. Два коврика
У другой хозяйки было два клетчатых коврика:
один размером 60 X 60 см, другой 80 X 80 см
(рис. 45). Она решила сделать из них один клетчатый
коврик размером 100 X Ю0 см. Мастер взялся
выполнить эту работу и пообещал, что каждый коврик
будет разрезан не более чем на две части и при
этом не будет разрезана ни одна клетка. Обещание
свое он сдержал. Как он поступил?
89. Коврик с розами
На коврике (рис. 46) изображено 7 роз. Требуется
тремя прямыми линиями разрезать коврик на
7 частей, каждая из которых содержала бы по одной
розе.
46 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ
—
90. Квадрат на 20 равных треугольников
Разрезать квадратный кусок бумаги на 20 равных
треугольников и сложить из них 5 равных квадратов.
91. Из креста—квадрат
Крест, составленный из пяти квадратов, требуется
разрезать на такие части, из которых можно было
бы составить один квадрат.
92. Из квадрата — три квадрата
Разрезать квадрат на семь таких частей, чтобы
сложив их надлежащим образом, получить три равных
квадрата.
Эту задачу, можно обобщить:
1. Разрезать квадрат на такие части, из которых
можно было бы составить данное число равных
квадратов.
2. Разрезать квадрат на наименьшее число частей,
которые, соответственно сложенные, давали бы
некоторое число равных между собою квадратов.
93. Из квадрата — два квадрата
Разрезать квадрат на 8 таких частей, чтобы, сложив
их соответственным образом, получить два
квадрата, площадь одного из которых была бы вдвое
больше площади другого.
94. Из квадрата — три квадрата
Разрезать квадрат на такие 8 частей, чтобы, соответственно
сложенные, они составили 3 квадрата,
площади которых были бы пропорциональны числам
2* 3 и 4,
95. Из шестиугольника — квадрат
Разрезать правильный шестиугольник на 5 таких
частей, чтобы, соответственно сложенные они образовали
квадрат*
47 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. VII. УПРАЖНЕНИЯ С КУСКОМ БУМАГИ