Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XI. ДОМИНО

Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
XI. ДОМИНО
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.

Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. XI. ДОМИНО (стр. 75-82)

Текст для быстрого ознакомления:

XI. ДОМИНО

Историческая справка
Предполагают, что игра «домино» перешла к нам
от индусов или древних греков. Действительно, простота
этой игры наводит на мысль, что она придумана
еще в очень отдаленные времена, на первых ступенях
цивилизации, Что касается названия самой
игры, то относительно него существуют разногласия.
Филологи ищут его корень в древних языках, но вероятнее
всего такое предположение. Игра в домино
разрешалась в католических монастырях и религиозных
общинах. Но всякое дело там начиналось, как
известно, с восхваления «имени божия». И когда
игрок выставлял первую кость, он произносил: «Ьепе-
dicamus Domino» (бенедикамус Домино), т. е. «восхвалим
господа». Или произносилось «Domino gratias
» (Домино гратиас), т. е. «благодарение господу
». Отсюда и получилось в сокращении просто слово
«домино».

75  Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XI. ДОМИНО

131. Удивительный отгадчик
Десять косточек домино вниз «лицом» положены
в последовательно возрастающем справа налево по-
# рядке, т. е. одно, два, три и т. д. до десяти очков.
«Отгадчик» объявляет остальным, что он уйдет в
другую комнату или отвернется, а они без него могут
переместить справа налево сколько угодно косточек,
причем единственным условием ставится то, чтобы
не изменялось относительное расположение как перемещенных,
так и остальных косточек. По возвращении
отгадчик берется узнать не только число перемещенных
косточек, но и открыть ту косточку, которая
укажет (числом очков), сколько перемещено косточек.
И действительно, оказывается, что требуемую
косточку всегда можно открыть. Но для этого не
нужно даже «догадки», а достаточно самого простого,
не выходящего из предела первого десятка, арифметического
расчета.

 

Разъясним подробно задачу. Для этого перевернем
косточки домино «лицом» вверх. Справа налево
они первоначально лежат в таком порядке, как указано
на рис. 59,

76 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XI. ДОМИНО

Воображаемый «маг и чародей» оставляет комнату,
а тот, кто желает убедиться в «чудесных» его
способностях, перемещает несколько косточек справа
налево, не изменяя их относительного расположения,
а затем двигает все косточки в этом новом порядке
так, чтобы весь ряд косточек занимал прежнее место.
Пусть, например, перемещено вначале 4 косточки.
Тогда новый порядок их будет представлен на
рис. 60.
Очевидно, что первая косточка слева четверка и
показывает число перемещенных косточек. Поэтому
явившийся в комнату «угадчик» открывает первую

мещено
четыре косточки домино». Здесь могут быть
для большего интереса пущены в ход маленькие хит-
трости. Хотя дело в том, чтобы посхмотреть эту первую
косточку слева, но «угадчик» может сделать вид
и внушить собеседникам, что он знает число перемещенных
косточек раньше, чем открывает косточку, и
что открывание четверки есть только добавочное доказательство
его всезнанья.
Дальше дело пойдет еще удивительнее и занимательнее.
Косточки остаются в том же порядке, и угадывающий
уходит, зная, что последняя косточка слева
есть четверка. Сколько бы косточек в его отсутствие
ни переместили (опять справа налево и не
изменяя порядка), если он придет и откроет пятую
косточку (4 + 1 = 5 ) , считая слева направо, то число-
очков этой косточки покажет ему всегда число перемещенных
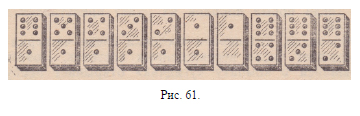
косточек. Так, пусть перемещено во второй
его выход справа налево три косточки. Тогда получится
такой порядок косточек, какой показан на
рис. 61, и пятая косточка, считая слева, действительно
показывает три очка. Открыв эту тройку и положив
ее опять на место, нетрудно уже, не глядя, сообразить,
что последняя косточка слева теперь будет

77 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XI. ДОМИНО

семерка. Запомнив это, угадывающий опять уходит в
другую комнату, предлагая перегостить сколько
угодно косточек справа налево, заранее зная, что по
приходе он откроет восьмую косточку и число очков
этой косточки ему покажет, сколько косточек было
перемещено в его отсутствие.

Вообще, если вы знаете число очков последней
слева косточки, а это, видим, нетрудно, то к этому
числу надо прибавить единицу, и вы получите’ то
место, считая по порядку слева, на котором лежит
косточка, указывающая, сколько косточек перемещено.
Но легко видеть, что для к а ж д о й косточки
сумма числа очков на ней и ее номера как раз равна
номеру косточки, которую нужно открыть в следующий
раз (если сумма больше 10, то из нее нужно
вычесть 10). Это упрощает все рассуждения. Теперь
достаточно лишь к числу очков открытой
косточки прибавить ее номер, чтобы получить номер
(быть может после вычитания 10) косточки, которую
нужно открыть в следующий раз. В рассмотренном
примере открывалась пятая косточка, на которой
были три очка. Значит после прихода нужно взять
восьмую (5 + 3 = 8) косточку.
Задача эта, как видим, весьма проста, но и весьма
эффектна. Разобраться в решении ее не составляет
особого труда, и каждый желающий может это
сделать.
132. Верная отгадка
Возьмите двадцать пять косточек домино, переверните
их «лицом» вниз и положите рядом одна за
другой так, чтобы они соприкасались более длинными
сторонами. Вслед за тем объявите, что вы отвернетесь
или даже уйдите в другую комнату, а кто-

78 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XI. ДОМИНО

нибудь пусть с правого конца переместит на левый
какое-нибудь число косточек домино (не более, однако,
двенадцати). Возвратившись в комнату, вы сразу
открываете косточку, число очков которой непременно
укажет число перемещенных в ваше отсутствие
косточек домино.
Как зто сделать?

133. Сумма всех очков домино

Сосчитайте сумму очков, содержащихся на всех
косточках домино.

134. Небольшая забава

Переверните «лицом» вниз все косточки домино
без дублей. Одну же из косточек тихонько спрячьте,
наблюдая только, чтобы эта косточка не была дублем.
Затем предложите кому-нибудь взять любую из
лежащих на столе косточек, посмотреть ее и положить
на стол вверх лицевой стороной, а вслед за
тем пусть он же раскроет и все остальные косточки
домино и расположит их вместе с первой открытой
косточкой по правилам игры, но так, чтобы не замкнуть
игры. Получится некоторое расположение косточек,
и вы сможете заранее предсказать числа
очков, которые получатся на концах этого расположения.
Эти числа будут как раз те, которые находятся
на квадратиках раньше спрятанной нами косточки
домино.
В самом деле, если расположить все косточки
домино одну за другой в порядке, требуемом правилами
игры, т. е. чтобы последовательные косточки
соприкасались квадратиками с одинаковым числом
очков, то игра всегда окончится таким же числом
очков, каким она началась. Если, скажем, расположение
косточек начинается квадратиком с пятью
очками, то оно и окончится пятью при условии, конечно,
не закрывать игру, пока не будут положены
все косточки. Итак, все 21 косточки без дублей можно
расположить, соблюдая правила игры, по кругу, и
если из этого круга отнять, например, косточку (3, 5),
то ясно, что расположение остальных 20 косточек
начнется с одной стороны пятьюг а окончится тремя*

79 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XI. ДОМИНО

Этой небольшой забавой вы можете очень заинтересовать
тех, кто не знает, в чем дело, особенно если
сделать вид, что вы будто бы производите в уме самые
сложные вычисления. Следует также при повторении
забавы по возможности ее разнообразить и
видоизменять.
135. Наибольшее число
Допустим, что играют в домино четверо. Каждый
играет «за себя», т-. е. на каждого игрока ведется
отдельный счет выигранных очков. Перед началом
игры каждый игрок имеет по семи косточек. При
атом могут получаться такие интересные расположения
косточек, при которых первый ирок обязательно
выигрывает, в то время как второй и третий игроки
не смогут положить ни одной косточки. Пусть, например,
у первого игрока будут четыре первых нуля и
три последних единицы, т. е. такие косточки:
(О, 0), (0, 1), (0, 2), (0, 3), (1,4), (1,5), (1,6),
а у четвертого игрока пусть будут остальные единицы
и нули, т. е. косточки
(1, 1), (1,2), (1,3), (0,4), (0, 5fc (0, 6)

и еще какая-либо косточка. Остальные косточки домино
поделены между вторым и третьим игроками.
В таком случае первый игрок выигрывает после того,
как будут положены все 13 указанных выше косточек
домино, а второй и третий игроки не смогут поставить
ни одной из своих.
В самом деле, первый игрок начинает игру и ставит
(0,0). Второй и третий досадуют, ибо у них нет
подходящей косточки. Тогда четвертый игрок может
положить любую из трех косточек (0,4), (0,5) или
(0,6). Но первый приложит в ответ (4,1), (5,1) или
(6,1). Второй и третий опять не смогут ничего положить,
а четвертый поставит (1,1) или (1,2), или (1,3),
на что первый может ответить (1,0), (2,0), (3,0)
и т. д. Таким образом, он положит все свои косточки, в
то время как у второго и третьего игроков останутся
все их косточки, а у четвертого — одна. Сколько же
выигрывает первый? Сумма очков в положенных 13

80 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XI. ДОМИНО

косточках равна, как легко видеть, 48, а число очкое
всей игры есть 168. Значит, первый игрок выигрывает
168 — 48 = 120 очков в одну игру. Это наибольшее
возможное число.
Можно составить и другие партии, подобные предыдущей.
Для этого стоит только нули и единицы
заменить соответственно косточками с иным количеством
очков: 2, 3, 4, 5 или 6. Число подобных партий,
следовательно, равно числу всех простых сочетаний
из семи элехментов по 2, т. е. равно 21. Ясно, что вероятность
получить такую партию случайно весьма
мала. Кроме того, все остальные партии, за исключением
приведенной выше, дадут меньшее, чем 120,
число выигранных очков.
136. Квадрат из 8 косточек
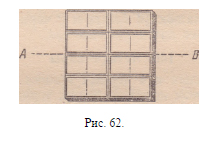
Можно ли из 8 косточек домино сложить квадрат
такой, что любая проведенная через него прямая пересекает
хотя бы одну косточку? Квадрат, изображен-

ный на рис. 62 не годится, так как прямая АВ не пересекает
ни одной косточки.
137. Квадрат из 18 косточек
Можно ли из 18 косточек домино сложить квадрат,
удовлетворяющий условию предыдущей задачи?
138. Прямоугольник из 15 косточек
Можно ли из 15 косточек домино сложить прямоугольник,
удовлетворяющий условию задачи 136?

82 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XI. ДОМИНО

Домино в математике. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. XI. ДОМИНО.

На главную страницу Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.

ДОМИНО