Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.

Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов.XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ(стр. 82-123)

Текст для быстрого ознакомления:

XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

167. О пауке и мухе
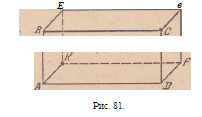
На потолке в углу С комнаты (рис. 81) сидит
паук, а на полу в противоположном углу К спит муха.

Какой путь должен избрать паук, чтобы добраться
до мухи по кратчайшему расстоянию?.

98 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

МОСТЫ И ОСТРОВА
Не приходилось ли вам жить, а может быть, вы
и сейчас живете в городе или местности, где течет
река, которая делится на протоки и рукава, образующие
острова? Через реку и ее протоки переброшены,
быть может, мосты, соединяющие различные части
города. В Ленинграде, например, очень много подобных
протоков, разветвлений Невы и разных каналов,
через которые переброшено весьма большое количество
мостов и переходов. Не приходила ли вам когда-
нибудь в голову мысль (если, конечно, вы живете в
местности, где есть река, острова и мосты) совершить
такую прогулку, чтобы во время ее перейти все эти
мосты, но перейти их так, чтобы на каждом побывать
только по одному разу? Вряд ли вы думали об этом,
а между тем мы стоим здесь перед весьма интересной
и важной задачей, поставленной впервые знаменитым
математиком Эйлером.
Поучительная сторона предлагаемых ниже задач
состоит в исследовании, возможно или нет решение
данной задачи, прежде чем приниматься за само решение.
Эйлер, в частности, подробно исследовал случай
невозможности.

168. Задача Эйлера
Задача, предложенная Эйлером в 1759 году, заключается
в следующем.
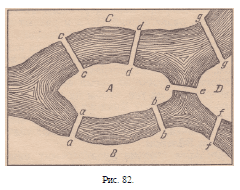
Река, огибающая остров, делится на два рукава,
через которые переброшено семь мостов: а, Ь, с, dy е,
f, g (рис. 82). Спрашивается, можно ли совершить
такую прогулку, чтобы за один раз перейти через все
эти мосты, не переходя ни через один мост два или
более раз?
— Это вполне возможно! — скажет кто-нибудь.
— Нет, это невозможно! — скажет другой.
Но кто прав и кто нет и как это доказать?
Самый простой путь решения задачи, казалось бы,
такой: сделать все возможные пробы таких переходов,
т. е. перечислить все возможные пути, и затем
рассмотреть, какой или какие из них удовлетворяют
условиям вопроса. Но очевидно, что даже в случае
только семи мостов приходится делать слишком

99 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

много таких проб. А при увеличении числа мостов
такой способ решения практически совершенно немыслим.
Да, кроме того, при одном и том же числе
мостов задача изменяется в зависимости еще от расположения
этих мостов. Поэтому изберем иной, более
надежный путь решения задачи.

Прежде всего исследуем, возможен или нет искомый
нами путь для данного расположения семи мостов.
Для облегчения рассуждений введем такие условные
обозначения:
Пусть Л, В, С и D будут разные части суши,
разделенной рукавами реки (рис. 82).
Затем, переход из места А в место В мы будем
обозначать через АВ — все равно, по какому бы
мосту мы ни шли, по а или по Ь. Если затем из В
мы перейдем в D, то этот путь обозначим через BDy
а весь переход, или путь из А в D, обозначим через
ABD, так что здесь В одновременно обозначает и
место прибытия и место отправления.
Если теперь из D перейдем в С, то весь пройденный
путь обозначим через ABDC. Итак, это обозначение
из четырех буке показывает, что из места А
мы, пройдя места В и D, пришли в С, причем перешли
три моста.
Значит, если мы перейдем четвертый мост, то
для обозначения пути нам понадобится пять букв.
После перехода следующего, пятого моста понадобит

100 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

ся обозначить пройденный путь шестью буквами
и т. д.
Словом, если мы обошли по одному разу все семь
данных мостов, то наш путь должен был бы обозначаться
восемью буквами (вообще, если есть п мостов,
то для обозначения искомого нами пути через
эти мосты понадобится п + 1 буква).
Но как и в каком порядке должны идти буквы
в этом обозначении?
Между берегами А и В есть два моста. Значит,
последовательность букв АВ или ВА должна быть
два раза. Точно так же два раза должно повторяться
соседство букв А и С (между этими местами
тоже два моста). Затем, по одному разу должно
быть соседство букв А и Д В и Д D и С.
Следовательно, если предложенная задача разрешима,
т. е. можно мосты перейти так, как требуется
задачей, то необходимо:
1) чтобы весь путь обозначался восемью буквами;
2) чтобы в расположении этих букв соблюдались
указанные условия относительно соседства и повторяемости
букв.
Разберемся теперь в следующем весьма важном
обстоятельстве.
Возьмем, например, местность Л, соединенную с
другими местностями несколькими мостами: а, 6,
с, … (в данном случае пятью мостами). Если мы
перейдем мост а (все равно откуда, из Л или из
В), то в обозначении пути буква Л появится один
раз. Пусть пешеход перешел 3 моста а, b и су ведущие
в Л. Тогда в обозначении пройденного пути буква
Л появится два раза, в чем нетрудно убедиться.
Если же на Л ведут 5 мостов, то в обозначении
пути через все эти мосты буква Л повторится 3 раза.
Вообще, легко вывести, что если число мостов, ведущих
в Л, есть нечетное, то, чтобы узнать, сколько
раз в обозначении требуемого пути повторится буква
Л, надо к этому нечетному числу мостов прибавить
единицу и полученное число разделить пополам.
То же, конечно, относится и ко всякой иной местности
с нечетным числом мостов, которую для краткости
будем называть нечетной местностью.
Усвоив все предыдущее, приступим к окончательному
исследованию задачи Эйлера.

101 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

В местность А ведет пять мостов. В каждую из
местностей В, С и D ведет по три моста. Значит,
все эти местности нечетные, и на основании только
что сказанного в обозначение полного пути через все
семь мостов необходимо, чтобы
у * 5+1 о
буква А вошла—^—* т*е* 3 раза;
буква В вошла ‘Цр-. т.е. 2 раза;
буква С вошла т.е. 2 раза;
буква D вошла——3, +т.1 е. 2 раза;
В с е г о 9 букв.
Получается, таким образом, что в обозначение искомого
пути обязательно должно войти 9 букв. Но мы
уже доказали выше, что в случае возможности решения
задачи весь путь должен обозначаться только
восемью буквами. Итак, задача для данного распо-
ложения семи мостов неразрешима.
Значит ли это, что задача о переходе по одному
разу через мосты неразрешима всегда, когда имеется
один остров, два рукава реки и семь мостов? Конечно
нет. Доказано только, что задача неразрешима
для данного располооюения мостов. При ином расположении
этих мостов и решение могло бы быть иное.
Теперь аке заметим, что во всех тех случаях, когда
число мостов, ведущих в различные места, нечетное,
можно применять рассуждения, совершенно
аналогичные предыдущим, и, таким образом, убедиться
в возможности или невозможности решения
задачи.
Чтобы перейти к решению более общей задачи,
необходимо рассмотреть случаи, когда имеется четное
число мостов, ведущих откуда-нибудь в другие
места.
Пусть, например, из места А переброшено через
реку четное число мостов. Тогда при обозначении
пути перехода через все мосты по одному разу надо
различать два случая: Г) начинается ли путь из А
или 2) из другого места.

102 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

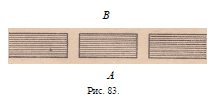
В самом деле, если из А в 5, например, ведут
два моста (рис. 83), то путник, отправившийся из Л
и прошедший по одному разу оба моста, должен
свой путь обозначать так: ЛВЛ, т. е. буква Л повторяется
два раза. Если же путник пройдет через те
же два моста, но из места В, то буква Л появится
всего один раз, ибо этот путь обозначится через
ВАВ.

Предположим теперь, что в Л ведут четыре мос*
та,— из одной ли местности или из разных, это все
равно. И пусть путник отправляется в обход по одному
разу всех мостов из места Л. Опять легко ви*
деть, что в таком случае при обозначении пройденного
пути буква Л повторяется три раза; но если
начать обход из другой местности, то буква Л повторится
только два раза. Точно так же в случае шести
мостов буква Л в обозначении всего пути повторится
четыре раза или три, смотря по тому, начался ли
переход из Л или из другой местности. Словом,
можно вывести такое правило:
Если число мостов известной местности четное
(четная местность); то в соответствующем обозначении
пути буква, обозначающая местность, появляется
число раз, равное половине числа мостов, если переход
начался из другой местности. Если, же переход
начался из самой четной местности, то число появлений
этой буквы равно половине числа мостов плюс
единица. В любом случае количество появлений
буквы, обозначающей четную местность, будет не
меньше, чем половина числа мостов, выходящих из
этой местности.
Предыдущие рассуждения позволяют вывести общий
прием решения каждой подобной задачи о мостах.
Во всяком случае мы можем сразу убедиться в
невозможности или возможности решения. Поступаем
следующим образом:

103 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

1) Отмечаем общее количество мостов и ставим
его в заголовке решения.
2) Обозначаем различные местности, разделенные
рекой, буквами Л, В, С, Z), … и пишем их в столбец
одну под другой.
3) Против каждой из местностей пишем во втором
столбце число всех ведущих из нее мостов.
Для случая рассмотренной нами задачи о семи
мостах будем иметь, значит, такую схему решения:
Число мостов 7
А 5
В 3
С 3
D 3
Заметим, что сумма чисел второго столбца всегда
точно равна двойному количеству мостов. Это следует
из того, что у каждого моста мы считаем оба его
конца, упирающиеся в различные берега. Кроме того,
если в задаче имеются нечетные местности, то количество
их четно, иначе второй столбец при сложении
не давал бы четного числа.
4) Припишем третий столбец, поставив в него половины
четных чисел второго столбца, а если во втором
столбце есть числа нечетные, то прибавляем к
ним единицу и пишем в третьем столбце половину
полученного числа. (Каждое число третьего столбца
не больше числа повторений соответствующей буквы
в обозначении пути.)
5) Находим сумму третьего столбца.
Для рассмотренной задачи имеем:
Число мостов 7
Л 5 3
В 3 2
С 3 2
D 3 2
9
Из сказанного следует, что всегда сумма третьего
столбца больше половины суммы второго столбца
(т. е. числа мостов) на половину количества нечет

104 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

ных местностей. С другой стороны, сумма третьего
столбца не больше суммы чисел повторений всех
букв, т. е. количества букв, обозначающих весь путь
(оно равно числу мостов плюс 1). Таким образом,
если задача разрешима, то половина количества нечетных
местностей не должна превышать единицы.
Мы установили в общем случае, что если задача
разрешима, то или
1) все местности четные,
или
2) нечетных местностей только две.
Далее мы увидим, что в этих случаях задача
о переходе по одному разу через мосты всегда разрешима
и в последнем случае обход нужно начинать
с одной из нечетных местностей.

169. Переход через 15 мостов
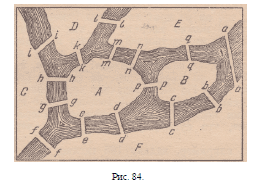
Решите теперь задачу, в которой четыре острова,
соединены между собой и с берегами реки 15 мостами,
как это показано на прилагаемом рисунке

(рис. 84). Можно ли за один раз обойти все эти
мосты, не проходя ни через один более одного раза?
Докажем теперь, что если все местности четные,
то существует замкнутый путь (кончающийся в
местности, с которой он начался), проходящий по

105 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

каждому мосту ровно один раз. Будем называть для-*
ной пути количество мостов, по которым этот путь проходит.
Так длина пути из решения задача 169 равна
15. Среди всех путей, которые можно провести по
нашим местностям с соблюдением условия задачи,
выберем самый длинный путь и обозначим его
abc … g (где буквы а, Ь, с, . . . , g — это названия мостов,
пересекаемых путем). Обозначим через А местность,
в которой он начинается, и предположим, что
он заканчивается в местности G, отличной от А. Если
путь ранее проходил через G, скажем, г раз, то,
двигаясь по нему, мы должны были уже пройти 2г
мостов, ведущих в G. Поскольку местность G четная,
то, войдя в нее по мосту g, мы должны найти еще
один мост Л, ведущий из G и отличный от уже пройденных
2г мостов и моста g. Это означает, что мы
можем продолжить путешествие и далее, в противоречие
с тем, что выбранный путь имеет максимальную
длину. Итак, путь abc … g кончается в местности
А, с которой начался, т. е. он замкнут. Покажем
теперь, что он проходит через каждый мост. Предположим,
что он не проходит через некоторый мост/\
Ясно, что f можно выбрать так, что через одну из
соединяемых им местностей проходит путь abc … g.
Для определенности предположим, что f ведет в
местность В, из которой выходят мосты а, Ь. Тогда
путь fbc … ga имеет длину, на единицу большую,
чем abc … g. Но мы обозначили через abc … g самый
длинный путь, который только можно провести
по нашим местностям. Полученное противоречие доказывает,
что путь abc … g проходит через’ все
мосты.
Так, например, задачу 168 можно было бы решить,
если бы задано было обойти все мосты по два
раза каждый, что сводится, в сущности, к удвоению
числа мостов, т. е. к обращению всех данных местностей
в четные.
Докажем теперь, что требуемый путь существует
и во втором случае, когда есть только две нечетные
местности, скажем, А и В. Построим новый мост а,
соединяющий А и В. Тогда все местности станут
четными и, по доказанному выше, существует путь,
проходящий по одному разу через все мосты. Этот
путь замкнут, следовательно, его можно начинать с

106 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

любого моста, например с моста a: abc … g. Легко
видеть, что путь Ьс … g, концы которого лежат в нечетных
местностях А и В, решает нашу задачу.
Исследовав задачу и сделав вывод о ее разрешимости,
остается только совершить самый обход мостов.
Но это уже сравнительно легкая часть задачи.
Тем более что в наших доказательствах содержится
и способ отыскания нужного пути.

170. Путешествие контрабандиста
Задачу о переходе через мосты можно предлагать
в различных видоизменениях. Можно представить ее,
например, как путешествие контрабандиста, который
решил побывать во всех странах Европы, но так,
чтобы через границу каждого государства ему пришлось
переходить только один раз.
В данном случае очевидно, что различные страны
и их границы будут соответствовать разным местностям
и рукавам реки, через которые переброшено по
одному мосту (для каждой границы, общей двум
странам).

171. О фигурах, вычерчиваемых одним росчерком
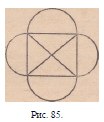
Известен анекдот: некто давал миллион рублей
каждому, кто начертит следующую фигуру (рис. 85),
Но при вычерчивании ставилось одно условие. Тре*
бовалось, чтобы фигура эта была
вычерчена одним непрерывным
росчерком, т. е. не отнимая пера
или карандаша от бумаги и не
удваивая ни одной линии, другими
словами, по раз проведенной
линии нельзя уже было пройти
второй раз.
Надежда стать «миллионером
», решив такую легкую зада-

чу, может заставить испортить
много бумаги и потратить много времени на попытки
вычертить эту фигуру, как требовалось, одним росчерком.
Задача, однако, не решается, и это тем досаднее,
что она не решается только «чуть-чуть». Никак
не удается провести только одной «последней»

107 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

какой-либо линии. Удается даже открыть секрет, что
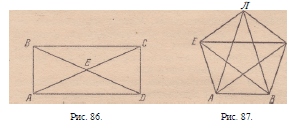
вся трудность в том, чтобы вычертить сначала одним
росчерком, не повторяя линии, еще более простую
фигуру — четырехугольник с двумя диагоналями
(рис. 86). Это, казалось бы, уже совсем просто, а все-
таки… не удается!..
Сомнения в невозможности решения этой задачи
все-таки остаются, тем более что фигуры, гораздо
более сложные и трудные с виду, легко вычерчиваются
одним росчерком. Так, например, выпуклый

пятиугольник со всеми его ‘диагоналями легко вычерчивается
одним непрерывным движением без повторения,
причем получается фигура, представленная
на рис. 87.
То же самое легко удается со всяким многоугольником
с нечетным числом сторон и никак не
удается с квадратом, шестиугольником и т. д.— словом,
с многоугольником с четным числом сторон.
Теперь нам нетрудно будет разобраться и показать,
какую из любых данных фигур можно вычертить
одним росчерком, без повторений линий, а какую
нет. Каждую из задач подобного рода можно
свести к разобранной уже нами Эйлеровой задаче о
мостах.
В самом деле, возьмем, например, четырехугольник
ABCD с двумя его диагоналями, пересекающимися
в Е (рис. 86). Можно ли его вычертить одним
непрерывным росчерком, без повторения линий?
Точки Л, В, С, D и Е мы представим себе как
центры некоторых местностей, разделенных рекой, а
линии, соединяющие эти точки,— как мосты, ведущие
в эти местности. Что же в данном случае получаем?

108 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

Пять местностей, из которых четыре нечетные и одна
четная. Мы знаем уже, что в таком случае нельзя
за один раз обойти все мосты, не переходя ни через
один два раза, или, другими словами,
нельзя обойти все данные точки одной
непрерывной линией без повторения
прежнего пути.

Случаи возможности и невозможности
вычерчивания одним росчерком
фигур совершенно те же, что и в задаче
о мостах. Одна задача, в сущности,
сводится к другой.
Всякий нечетный многоугольник со
всеми его диагоналями можно вычертить
одним росчерком без повторения линий потому,
что этот случай соответствует тому, когда данные
в задаче о мостах местности все четные.

Соображения, изложенные здесь, одинаково прилагаются
ко всякой фигуре, образована ли она прямыми
или кривыми линиями, на плоскости или в
пространстве. Так нетрудно видеть, что можно опи-
сать одним непрерывным движением все ребра
правильного октаэдра и нельзя этого сделать для
четырех остальных правильных выпуклых тел.
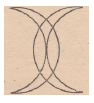
Говорят, что Магомет вместо подписи (он был
неграмотен) описывал одним росчерком состоящий
из двух рогов Луны знак, представленный на

109 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

110 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

мы имеем дело только с точками четного порядка, а
следовательно, вычертить такую фигуру одним росчерком
без повторения тех же линий всегда можно.
Всегда можно также вычертить одним росчерком и
такую фигуру, где, помимо точек четного порядка,
есть и две точки (но не более) нечетного порядка.
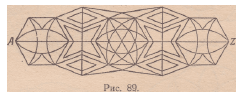
Весьма красивый и замысловатый образчик такой
фигуры’заключающий в себе две нечетные точки А
и Z, показан на рис. 89. С какой-нибудь из этих точек
и надо начинать непрерывное вычерчивание фигуры,
как мы уже знаем из задачи о мостах.
Нельзя вычертить одним росчерком фигуры, показанные
на рис. 90 и 91, при всей их видимой простоте,
так как в первой восемь, а во второй — двенадцать
точек нечетного порядка. Первая может
быть вычерчена не менее как четырехкратной, т. е,
состоящей из четырех непрерывных кусков, а вторая—•
не менее как шестикратной линией.
Таких примеров можно подобрать сколько угодно.
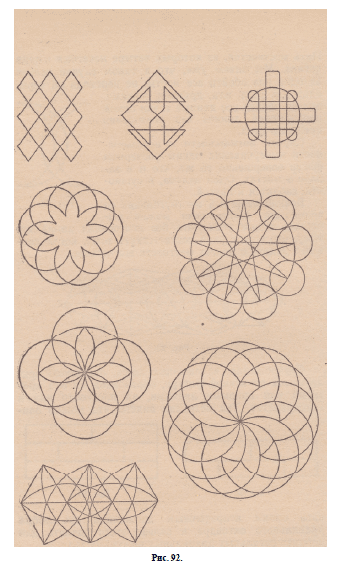
Для упражнения предлагаем читателю заняться
во время досуга вычерчиванием с одного росчерка
фигур, приведенных на рис. 92.

172. В мастерской
В мастерской имеется 10 различных станков. Известно,
что каждый из 10 рабочих этой мастерской
умеет работать только на двух станках и на каждом
станке умеют работать только два рабочих. Можно
ли расставить рабочих у станков так, чтобы каждый
стоял у станка, на котором умеет работать?

111 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ

Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Путешествие по стране геометрии. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИЙ.

На главную страницу Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.

ГЕОМЕТРИЯ ПУТЕШЕСТВИИ, Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИИ