Избранные в опросы теории преобразований подобия плоскости

Избранные в опросы теории преобразований подобия плоскости. § 1. Гомотетия, ее свойства и признак

З. А. Скопец, Л. И. Кузнецова

Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

§ 1. Гомотетия, ее свойства и признак

Определение гомотетии

к. Определение гомотетии
Зададим точку О в плоскости и число k ф 0. Рассмотрим отношение,
при котором образом точки X плоскости является такая
точка Xlt что ОХх — k O X .
Точка О в паре с любой точкой X определяет единственный
вектор О Х (рис. 5). Произведение вектора О Х и числа k есть вектор
k O X . В плоскости для точки О существует единственная точка Х х
такая, что О Х г = k O X . Следовательно, для любой точки X плоскости
при заданном отношении существует единственный образ.
Образом точки О является сама эта точка.
Пусть теперь — произвольная точка плоскости. Является
ли она образом какой-нибудь точки при заданном отношении?
Другими словами, существует ли такая точка Y , что выполняется
равенство OFx = kOY?
Так как по условию k ф 0, то из равенства ОУг = kOY следует
равенство OY = —OY±. Следовательно, каждая точка плоскости
k
является образом единственной точки плоскости при заданном отношении*
Таким образом, заданное отношение есть обратимое отображение
плоскости на себя. Это отношение называется гомотетией. Существенным
при задании гомотетии оказалось задание точки О и числа
k ф 0. Точка О называется центром гомотетии, а число k — ее
коэффициентом.

186 Гомотетия. Свойства Гомотетии.

О п р е д е л е н и е . ‘ Гомотетией е центром О и коэффициентом
k (k Ф 0) называется отображение плоскости на себя, при котором
образом точки X является такая точка Х1У что ОХг — kOX.
Запись ОХ± — kOX равносильна записи Н о ( Х ) = X v
При k — 1 выполняется равенство О Х г = О Х , т. е. Но — тождественное
преобразование. При k = —1 любая точка X отображается
на такую точку что О Х х — —О Х . Следовательно, гомотетия
с коэффициентом —1 есть центральная симметрия,
Б. Свойства гомотетии
1. Как видно из проведенных ранее рассуждений, гомотетия
является обратимым отображением плоскости на себя. Это значит,
что для гомотетии существует обратное ей отображение, причем
i_
отображение, обратное гомотетии Но, есть гомотетия Hoi
(Hko (X) =ХУ)<^ {ОХг= КОХ) ^ (ох =
Для гомотетии выполняются и другие свойства обратимых отображений,
в частности пересечение (объединение) фигур при гомо-
‘ тетии отображается на пересечение (объединение) их образов.
2. Т е о р е м а 1 . Если при гомотетии Нк
0 точки X и Y
отображаются на Х1 и Ylf то X1Y1 — k X Y ,
Д о к а з а т е л ь с т в о . Так как Х г — Н о { Х ) и Fi = Н % (У),
то по определению имеем:
О Х ± = k O X , OY^ kOY.’
Поэтому xTr, = 0Y1 — ОХг = kOY — kOX = k (OY — OX) = kXY,
что и требовалось доказать.
С л е д с т в и е . При гомотетии Но любые точки X и Y ото-
сражаются на такие точки Хг и Yly что | X1Y1 \ = |k\ \ XY|.
3. Важно выяснить, на какую фигуру отображаются при гомотетии
прямая, отрезок, луч, полуплоскость.
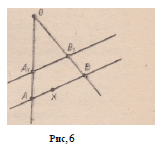
Пусть даны прямая А В и точка X на
ней, X ф А, X ф В (рис. 6). При гомотетии
Но точки А, В и X отображаются на А1У
Вг и Хг соответственно. Принадлежит ли
точка Х1 прямой А±В±?
Три точки принадлежат одной прямой,
если одна из этих точек лежит между дву-
ия другими. Следовательно, нужно выяснить,
лежит ли одна из точек А1з Вг и Х±
между двумя другими. Ответ на этот вопрос
дает следующая теорема.

187 Гомотетия. Свойства Гомотетии.

Т е о р е м а 2 . При гомотетии сохраняется отношение « лежать
между», т. е. если точка X лежит между точками А и В
и А1У Вг, Хх — образы точек А, В и X при гомотетии Н*ЬУ то Х±
лежит между Ах и Bv
Д о к а з а т е л ь с т в о . Так как X лежит между А и Я, то
точки X, А и В попарно различны (т. е.. \ А В \ Ф 0 , |А Х \ ф О,
\ Х В \ ф 0) и выполняется равенство | А Х \ + \ Х В \ ===. \ А В \ . После
умножения обеих частей этого равенства на \ k \ получим: \ k \ |ЛХ| +
+ \ k \ \ Х В \ = \ k \ \ А В \ или (по следствию из теоремы 1) \А1Х1\ +
-f- | X i B i | = | А1В11 и | А\Хг| ф 0, | Х ± В 11 ф 0, | А\В±\ ф 0, откуда
следует, что точка хг лежит между Аг и BL.
Пусть теперь дан отрезок А В — объединение различных точек
А и В и множества точек, лежащих между ними. Так как при гомотетии
объединение фигур отображается на объединение их образов
(свойство 1) и сохраняется отношение «лежать между» (теорема
2), то отрезок А В отображается на объединение образов Аг и Вг
точек Л и В и множества точек, лежащих между Аг и В1У т. е. на
отрезок А.В,. Следовательно, образом отрезка при гомотетии
является отрезок.
Луч А В можно рассматривать как объединение отрезка А В и
множества точек X, таких, что В лежит между Л и X. Учитывая
свойства гомотетии отображать объедийение фигур на объединение
их образов , и сохранять отношение «лежать между», находим, что
образом луча при гомотетии является луч.
Выясним,, на какую фигуру отображается при гомотетии прямая.
Для любых трех попарно различных точек Л, В и X прямой одна ‘
из них лежит между двумя другими. Тогда из точек А± = Но (Л),
Вг = Но (В) и Хх т= Но (X) также одна лежит между двумя другими,
т. е. Х1 6 (ЛА). Обратно, если Y1i(A1Bl\ то Y = (//5)_1(Кi)
принадлежит прямой АВ. Следовательно, прямая А1В1 есть
множество образов точек прямой АВ, т. е. образ прямой АВ.
Итак, прямая отображается при гомотетии на прямую.
Пусть а и ( 5 — полуплоскости с границей а, точка В принадлежит
полуплоскости (3, но не принадлежит прямой^. Полуплоскость
а можно рассматривать как объединение прямой а и множества точек
X, таких, что точки В и X разделены прямой а (пересечение
отрезка ВХ и прямой а есть точка). При гомотетии полуплоскость
а отобразится на объединение прямой аг — образа прямой а и •
множества точек Хх, таких, что точки Вг и Хг разделены прямой
а1У т. е. полуплоскость сс с границей а отображается на полуплоскость
а1 с границей аг.
Итак, мы показали, что образом отрезка, луча, прямой,, полуплоскости
при гомотетии является соответственно отрезок, луч,
прямая, полуплоскость.
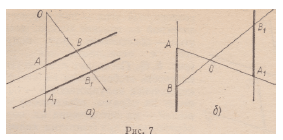
4. Прямая и ее образ при гомотетии параллельны; при k > 0
любой луч отображается на сонаправленный с ним луч (рис. 7, а)

188 Гомотетия. Свойства Гомотетии.

при k < О любой луч отображается на противоположно направленный
с ним луч (рис. 7 , 6 ) .
В самом деле, если А и В — точки прямой а > А х и В х — их
образы при гомотетии Н о * то А Х В Х = k A В (теорема 1), откуда следует,
что (Л^) || { А В ) \ [ A x B ^ W l A B ) при k >0и [АА) \ \ \ А В )
при k < 0.
5. Центр гомотетии, не являющейся тождественным преобразованием,
есть единственная неподвижная точка этого преобразования.
6. Прямая, проходящая через центр гомотетии, отображается
на параллельную ей и проходящую через центр гомотетии прямую,
т. е. на себя.
Выясним, только ли такие прямые будут при гомотетии двойными.
Если прямая а отображается на себя при гомотетии #о, k ф 1,
то для любой точки X 6 а образ ее = Но (X) также принадлежит
прямой а. Но точка и ее образ при гомотетии лежат на одной прямой
с центром, т. е. О 6 (^^i) = а-
Таким образом, прямые, проходящие через центр, и только они —
двойные прямые гомотетии, отличной от тождественного преобразования.
7. При гомотетии любой угол отображается на конгруэнтный
ему угол.
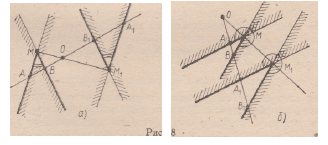
Всякий выпуклый угол можно рассматривать как пересечение
двух полуплоскостей с пересекающимися границами (рис. 8, а),

189 Гомотетия. Свойства Гомотетии.

выделенной
на границе точкой, невыпуклый,
угол — объединение двух полуплоскостей
с пересекающимися границами
(рис. 8,6). Поскольку при гомотетии полуплоскость
отображается на полуплоскость,
пересечение полуплоскостей — на пересечение
их образов, объединение полуплоскостей
— на объединение их образов, то
образом угла при гомотетии является угол.
Кроме того, при гомотетии каждый луч отображается
на сонаправленный с ним или на
противоположно направленный с ним луч.
А два выпуклых (невыпуклых) угла с соответственно
сонаправленными или соответственно
противоположно направленными
сторонами конгруэнтны, так как в первом
случае существует перенос, а во втором —
центральная симметрия, при которых
один угол отображается на другой.
Таким образом, угол и его образ при
гомотетии конгруэнтны.
8. Любой репер и его образ при гомотетии
одинаково ориентированы.
Д о к а з а т е л ь с т в о . Пусть задан
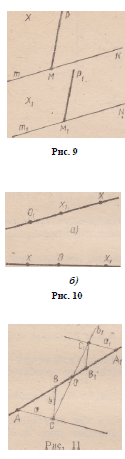
репер X — полуплоскость с границей т
и лучом MN на границе (рис. 9). Выберем
в полуплоскости еще луч МР. При гомотетии
с положительным коэффициентом
репер X отображается на Х±. При этом лучи
MN и МР отображаются на соответственно
сонаправленные с ними лучи М±М%
и MiPi (свойство 4). Но тогда существует
перенос, отображающий лучи MN и МР
на лучи M1N1 и M X P V Перенос, как было
отмечено вначале, не меняет ориентации
репера. Следовательно, реперы
X и Х г соориентированы.
При гомотетии с отрицательным коэффициентом репер X отображается
на Х 2 и существует центральная симметрия, отображаю-
щая^ репер X на Х2, т. е. реперы X и Х 2 также одинаково ориентированы.
9. Конструктивные способы задания гомотетии, ~
Как следует из определения, гомотетия однозначно задается
центром и коэффициентом. При этом либо центр, .либо коэффициент,
либо и центр, и коэффициент могут быть заданы опосредованно.
Например, если Но {X) == Х± и точки О, X и Хх заданы, то коэф-

190 Гомотетия. Свойства Гомотетии.

фйциент k можно найти из условия ОХ1 = k O X : |к \ = \ О Х г | : | О Х |;
и к > 0, если направления векторов О Х и О Х г совпадают (рис. 10, а),
k < 0, если направления векторов О Х и О Х х противоположны
(рис. 10, б).
Если Н о (X) = Х г и заданы точки X , Х г и число к , то точка
О может быть построена, так как из равенства О Х г = к О Х следует,
что точка О делит отрезок Х х Х в отношении k (считая до точки Х ± )
внутренним образом при к < 0 и внешним образом при k > 0
(см. рис. 10, а , б ) .
Если Н о (Л) = А г и Н о ( В ) = В и О £ ( А В ) (рис. 6), то Об ( A A J
и О 6 (55х), т. е. О = (ЛЛХ) П (B^iK а коэффициент & определяется
из условия О А х = £ОЛ.
Таким образом, гомотетия (с учетом ее свойств) может быть
однозначно задана:
а) центром и коэффициентом,
б) центром и парой соответственных точек {точки попарно различны
и лежат на одной прямой),
в) коэффициентом и парой соответственных точек,
г) двумя парами соответственных точек (Л; Лi), (5; £х), таких,
<//770 прямые А В и Л А параллельны и различны и \ А В \ Ф \ А 1 В 1 \ .
Возможны и другие способы задания.
З а д а ч а . Построить центр гомотетии, заданной двумя парами
точек (Л; Лх), (5; Bi), лежащих на одной прямой, А В ф А1В1
(рис. И).
Р е ш е н и е. Центр гомотетии можно построить, вычислив
предварительно ее коэффициент, исходя из равенства А г В г = k A B .
Более рационально, на наш взгляд, следующее решение.
Возьмем произвольную точку С $ { А В ) и проведем прямые
а = ( А С ) и b — { В С ) . При заданной гомотетии они отобразятся
на прямые а г и Ь 1 У параллельные а и b и проходящие через точки Лх
и В х соответственно. Пересечение фигур при гомотетии отображается
на пересечение их образов. Поэтому точка С — а [ } b отобразится
на С ± = а х П Ь ± . Точка О — (ЛЛХ) Г) ( С С г ) есть центр заданной
гомотетии. Так так А В Ф А±В1У то задача всегда имеет
и притом единственное решение.

В. Признаки гомотетии и параллельного переноса

При сравнении свойств параллельного переноса и гомотетии
(центральная симметрия — частный случай гомотетии) нетрудно
заметить, что при том и другом преобразовании любая прямая отображается
на параллельную ей прямую. Оказывается, никакие
другие преобразования, кроме гомотетии и переноса (тождественное
преобразование — частный случай гомотетии и переноса), данным
свойством не обладают.

191 Гомотетия. Свойства Гомотетии.

Т е о р е м а 3 . Преобразование плоскости,
при котором любая прямая
отображается на параллельную ей прямую,
есть либо гомотетия, либо параллельный
перенос.
Д о к а з а т е л ь с т в о . Пусть преобразование
/ отображает любую прямую
на параллельную ей, в частности
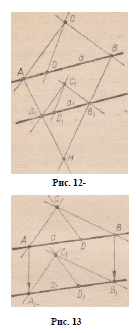
прямую а на аг¥=а (рис. 12). Для произвольных
точек А и В прямой а их образы
Аг и Вг принадлежат прямой ах.
Если С £ а, то она является точкой пересечения
прямых СА и СВ. Тогда образ
ее при преобразовании / есть точка
Сг, которая является пересечением прямых,
проходящих через точки Лх и Вх и
параллельных прямым С А и СВ соответственно.
‘
Пряхмые АА1 и BBL лежат в одной
плоскости и, следовательно, либо пересекаются,
либо параллельны. Рассмотрим
каждый из этих случаев.
1) ( А А ± ) Л ( В В г ) = М . ^ (рис. 12).
При гомотетии Н\^А^, заданной центром
М и парой точек (А; Лх), точка С
отображается на точку пересечения прямых,
проходящих через Лх и Вх и параллельных
(Л С) и ( В С ) соответственно,т. е. Н м ‘ ‘ A l ) ( С ) = /(С) = Сх
для С ~ £ а.
Если D £ а, то и при гомотетии Н(й,Ах\ и при преобразовании
f точка D отображается на точку пересечения прямой ах и прямой,
-проходящей через точку Сг и параллельной прямой CD, т. е.
Н $ А ) ( D ) = / (D) = D t .
Таким образом, для любой точки X плоскости имеем: H m ‘ A i ) ( X ) =
= f ( X ) — X l t а значит, / = Hu’Al). При этом /( М ) = Н м ’ А ‘ ] ( М ) — М .
2 ) ( A A J П ( B B J = 0 (рис. 13). Нетрудно установить, что
в этом случае лучи А А Х и ВВХ сонаправлены и \ А А г \ = | ВВХ|,
т. е. ЛЛХ = . В В г . При переносе, заданном парой точек (Л; Лх),
любая точка С а , С = ( А С ) П ( В С ) , отображается на точку пересечения
прямых, проходящих через точки Л и В и параллельных
( А С ) и (ВС) соответственно. Следовательно, для точек С, не принадлежащих
прямой а , /(С) = АЛх (С) = Сх.
Если D £ а , то и при переносе А А Л , и при преобразовании /
точка D отображается на точку пересечения прямой а х и прямой,
проходящей через точку С х и параллельной прямой C D . СледоваРис

192 Гомотетия. Свойства Гомотетии.

тельно, и для точек D прямой а А А Х (D) =
= f ( D ) = D l .
Таким образом, для любой точки X плоскости
имеем: А А г (X) = f ( Х ) — = Х 1 , а значит,
/ = А А г .
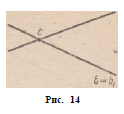
Мы рассмотрели случай, когда прямые
а и аг = / ( а ) различны. Если таких прямых
не найдется, т. е. любая прямая и ее Рис. 14
образ при преобразовании /совпадают, то
f — тождественное преобразование. Действительно,
любая точка С может быть рассмотрена как
точка пересечения двух прямых, например а и b (рис. 14).

По условию / ( а ) = а и / (bj = b. Тогда / ( с ) = / ( а Л Ь ) = f ( а ) f|
П f ( Ь ) = а { ] b = С.
Тождественное преобразование — частный случай гомотетии и
параллельного переноса.
Итак, теорема доказана.
Учитывая доказательство теоремы 3, можно сформулировать следующие
признаки гомотетии и параллельного переноса.
Преобразование плоскости, при котором любая прямая отображается
на параллельную ей прямую и прямые, проходящие через точку
и ее образ, принадлежат одному центральному пучку, есть гомотетия.
Преобразование плоскости, при котором любая прямая отображается
на параллельную ей прямую и прямые, проходящие через
точку и ее образ, принадлежат одному пучку параллельных (попарно
паралмльных), есть параллельный перенос.

193 Гомотетия. Свойства Гомотетии.

Похожие статьи:
Школьная Математика. Школьный курс математики. Школьная математика скачать. Школьные учебники по математике.
Школьные задачи по математике. Математика 1 класс. Математика 2 КЛАСС. Математика 3 КЛАСС. 

Гомотетия, свойства Гомотетии