Глава I. ПЯТОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ. 10000 действий в секунду.
ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман ИЗДАНИЕ ДВЕНАДЦАТОЕ СТЕРЕОТИПНОЕ
Под редакцией и с дополнениями В. Г. Болтянского
Скачать 11-ое издание ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман в формате PDF в хорошем качестве, но без возможности каптирования на Главной странице ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Текст для быстрого ознакомления (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):
10000 действий в секунду
Замечательно, что триггерные схемы позволяют
также производить действия над числами. Рас-
смотрим, например, как можно осуществить сложе-
ние двух чисел.
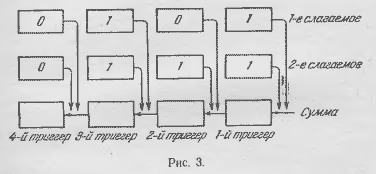
Пусть три цепочки триггеров соединены так, как
указано на рис. 3. Верхняя цепочка триггеров служит
для записи первого слагаемого, вторая цепочка — для
записи второго слагаемого, а нижняя цепочка — для
получения суммы. В момент включения прибора на
триггеры нижней цепочки приходят импульсы от тех
триггеров верхней и средней цепочек, которые нахо-
дятся в положении 1.
Пусть, например, как это указано на рис. 3, в
первых двух цепочках записаны слагаемые 101 и 111
(двоичная система счисления). Тогда на первый (са-
стр. 20 10000 действий в секунду.
ыый правый) триггер нижней цепочки приходят (в moj
мент включения прибора) два импульса: от первых
триггеров каждого из слагаемых. Мы уже знаем, что
в результате получения двух импульсов первый триг-
гер останется в положении 0, но даст ответный им-
пульс на второй триггер. Кроме того, на второй триг-
гер приходит сигнал от второго слагаемого. Таким
образом, на вт/арой триггер приходят два импульса,
вследствие чего второй триггер окажется в положе-
нии 0 и пошлет ответный импульс на третий триггер.
Кроме того, на третий триггер приходят еще два им-
пульса (от каждого из слагаемых). В результате по-
лученных трех сигналов третий триггер перейдет
в положение 1 и даст ответный импульс. Этот ответ-
ный импульс переводит четвертый триггер в положе-
ние 1 (других сигналов на четвертый триггер не по-
ступает). Таким образом, изображенный на рис. 3
прибор выполнил (в двоичной системе счисления)
сложение двух чисел «столбиком»:
или в десятичной системе: 5 + 7= 12. Ответные им-
пульсы в нижней цепочке триггеров соответствуют
тому, что прибор как бы «запоминает в уме» одну
единицу и переносит ее в следующий разряд, т. е.
выполняет то же, что мы делаем при сложении «стол-
биком».
Если бы в каждой цепочке было не 4, а скажем,
20 триггеров, то можно было бы производить сло-
жение чисел в пределах миллиона, а при большем
числе триггеров можно складывать еще большие
числа.
Заметим, что в действительности прибор для вы-
полнения сложения должен иметь несколько более
сложную схему, чем та, которая изображена на рис. 3.
В частности, в прибор должны быть включены осо-
бые устройства, осуществляющие «запаздывание»
сигналов. В самом деле, при указанной схеме при-
бора сигналы от обоих слагаемых приходят на пер-
вый триггер нижней цепочки одновременно (в
момент включения прибора), В результате оба
стр. 21 10000 действий в секунду.
сигнала сольются вместе и триггер воспримет их как
один сигнал, а не как два. Во избежание этого ну-
жно, чтобы сигналы от слагаемых приходили не одно-
временно, а с некоторым «запаздыванием» один после
другого. Наличие таких «запаздывании» приводит к
тому, что сложение двух чисел требует большего вре-
мени, чем регистрация одного сигнала в триггерном
счетчике.
Изменив схему, можно заставить прибор выпол-
нять не сложение, а вычитание. Можно также осуще-
ствить умножение (оно сводится к последовательному
выполнению сложения и поэтому требует в несколько
раз больше времени, чем сложение), деление и дру-
гие операции.
Устройства, о которых говорилось выше, приме-
няются в современных вычислительных машинах. Эти
машины могут выполнять десятки и даже сотни ты-
сяч действий над числами в одну секунду! А в Неда-
леком будущем будут созданы машины, рассчитан-
ные на выполнение миллионов операций в секунду.
Казалось бы, что такая головокружительная скорость
выполнения действий ни к чему. Какая, например,
может быть разница в том, сколько времени машина
будет возводить в квадрат 15-значное число: одну
десятитысячную долю секунды или, скажем, четверть
секунды? И то и другое покажется нам «мгновенным»
решейием задачи…
Однако не спешите с выводами. Возьмем такой
пример. Хороший шахматист, прежде чем сделать
ход, анализирует десятки и даже сотни возможных
вариантов. Если, скажем, исследование одного ва-
рианта требует нескольких секунд, то на разбор сотни
вариантов нужны минуты и десятки минут. Нередко
бывает, что в сложных партиях игроки ибпадают в
«цейтнот», т. е. вынуждены быстро делать ходы, так
как на обдумывание предыдущих ходов они затра-
тили почти все положенное им время. А что, если ис-
следование вариантов шахматной партии поручить
машине? Ведь, делая тысячи вычислений в секунду,
машина исследует все варианты «мгновенно» и ни-
когда не попадет в цейтнот…
Вы, конечно, возразите, что одно дело— вычисле-
ния (хотя бы и очень сложные), а другое дело — игра
стр. 22 10000 действий в секунду.
в шахматы: машина не может этого делать! Ведь
шахматист при исследовании вариантов не считает,
а думает! Не будем спорить: мы еще вернемся к
этому вопросу ниже.
стр. 23 10000 действий в секунду.
На главную страницу ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Школьная математика. Математика в школе.




Comments