Формирование математического мышления

Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.

Ю. М. Колягин. Д. С. Зейналов

ВОПРОСЫ МЕТОДИКИ ПРЕПОДАВАНИЯ ЗАДАЧ В ОБУЧЕНИИ ГЕОМЕТРИИ  (часть 5).
Формирование математического мышления

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

ВОПРОСЫ МЕТОДИКИ ПРЕПОДАВАНИЯ ЗАДАЧ В ОБУЧЕНИИ ГЕОМЕТРИИ.
Формирование математического мышления.

 

V. Для повышения эффективности развивающего обучения геометрии
перед учащимися следует систематически ставить серии
задач (или отдельные задачи), которые наряду с конкретными
обучающими функциями несли бы в себе (также в качестве ведущих)
функции, направленные на формирование у школьников элементов
творческого математического мышления.
В качестве таких задач могут выступать, например, задачи,
при постановке которых или в процессе решения которых:
учащимся мотивируется целесообразность изучения нового материала,
разумность определений геометрических понятий, полезность
изучения тех или иных теорем;
учащиеся побуждаются к самостоятельному открытию того или
иного геометрического факта, к обоснованию того или иного положения,
к установлению возможности применения уже усвоенных
ими знаний в новой для них ситуации;
учащиеся подводятся к самостоятельному открытию методов
доказательства теорем, общих приемов решения задач, к установлению
новых связей между известными им геометрическими понятиями;
у учащихся формируются умения использовать ведущие методы
научного познания (опыт, наблюдение, сравнение, анализ,
обобщение и т. д.) как методы самостоятельного изучения геометрии,
понимание роли и места индукции, аналогии дедукции в процессе
познания;
учащиеся обнаруживают взаимосвязь геометрии и алгебры с
другими предметами, устанавливают содержательные и структурные
связи между различными вопросами самого курса геометрии,
получают возможность применить математические знания к решению
нематематических задач;
учащиеся приобщаются к самостоятельным поисковым исследованиям
(посредством изучения результатов решения задач, изменения
условия задачи, возможных обобщений задачи, отыскания
других способов ее решения и отбора того из них, который наиболее
полно удовлетворяет заданным условиям, и т. п.);
у учащихся формируются качества, присущие научному мышлению
(активность, гибкость, глубина, критичность, доказательность
и т. п.), умение выражать свою мысль ясно и точно и т. д.
Практическая возможность использования вышеуказанных рекомендаций
обусловлена возможностью использовать для этой
цели задачи, похмещенные в учебниках. Незначительная методически

65 Формирование математического мышления

направленная обработка условия той или иной задачи, изменение
места и времени ее постановки существенно меняют дидактическую
значимость задачи, оставляя неизменным ее фактическое содержание.
Рассмотрим следующую задачу: «Даны (рис. 4) IAD) — биссектриса
Z-BAC, \АВ\ = |АС\. Доказать: |DC| = |J3D|».
Для учащихся 6 класса, приступающих к ее решению сразу
после изучения признаков конгруэнтности треугольников, эта
задача реализует только обучающие функции.
Видоизменим эту задачу: «Известно, что IAD) — биссектриса
Z.ВАС, \АВ\ — [АС|. Конгруэнтность каких элементов из этого
следует?» Тем самым мы переводим эту задачу в число задач проблемного
характера, методически более содержательных. В процессе
решения эта задача естественно трансформируется в задачу,
предложенную учебником.
Рассмотрим следующую задачу:
«Даны (рис. 5) [ADI П 1ВС] = Е, \ВЕ\ = |£С|. \АЕ\ =\ED\.
Доказать: ААВЕ ^ ACED».
Эта задача также обучающая. Видоизменим эту задачу: «Каких
данных достаточно для того, чтобы доказать конгруэнтность треугольников
А BE и CED (рис. 5)?»
Тем самым задача также становится проблемной.
При воспитании у учащихся творческой активности нередко
можно использовать и те задачи, которые уже стали традиционными
в школьном обучении. Такова, например, следующая известная
задача: «Даны прямая PH и две точки Л и В по одну сторону от этой
прямой. На прямой PH найти такую точку С, чтобы сумма расстояний
\АВ[ + \ СВ \ была минимальной».
Приведем ту же задачу в иной формулировке: «По одну сторону
канала находятся два населенных пункта. Найдите на берегу этого
канала место для постройки насосной стацции, которая снабжала
бы водой оба данных пункта». Заметим, что минимальность суммы
расстояний, по которым будут проложены трубы, уже явно не оговорена,
она вытекает из смысла самой задачи; но для того,, чтобы
это установить, школьники должны проявить творческую активность.
Заметим, что хорошим аналогом этой задачи является задача на
отражение света от плоской зеркальной пластинки.

66 Формирование математического мышления

Понятно, что те или иные элементы развития формируются у
школьников в процессе решения каждой нетривиальной задачи.
Однако время от времени полезно осуществлять вместе с учащимися
достаточно детальное изучение особенностей некоторой задачи, подходов
к ее решению, обучать школьников планированию поиска решения
задачи, аргументации выбора тех или иных направлений решения.
Проиллюстрируем сказанное на примере следующей задачи (по
курсу геометрии 8 класса), нахождение верного решения которой
было обусловлено правильно организованным поиском и воспроиз- .
ведением знаний и умений, достаточных для ее успешного решения:
«Построить угол, величина которого равна половине величины
данного угла, не проводя непосредственного деления данного угла
на два конгруэнтных угла».
Определяющее значение в ходе поиска решения имела постановка
следующего вопроса: «Какие теоремы, связывающие один угол
с другим, известны?» Возможные ответы учащихся на этот вопрос:
а) во всяком треугольнике величина внешнего угла больше величины
внутреннего, с ним не смежного;
б) сумма величин внутренних углов треугольника равна 2d; *
в) величина внешнего угла треугольника равна сумме величин
углов треугольника, не смежных с ним;
г) в равнобедренном треугольнике углы при основании конгруэнтны;
д) свойства величин углов в круге (вписанных, центральных).
Критическая оценка выявленных теоретических положений
привела одних учащихся к отбору непосредственно тех, которые
сразу давали искомое решение (величина вписаннцго угла вдвое
меньше величины центрального угла, опирающегося на ту же дугу),
а других учащихся — к качественной переработке известных им
утверждений в частное утверждение, также дающее искомое (но
иное) решение задачи (величина внешнего угла при вершине равнобедренного
треугольника вдвое больше величины угла при его
основании).
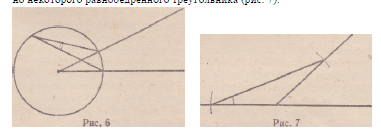
Найденные ключевые теоретические положения определили выбор,
приемлемого в данных условиях, метода решения (построения
с помощью циркуля и линейки) к стратегии решения: изображение
данного угла в виде центрального (рис. 6) или внешнего, относительно
некоторого равнобедренного треугольника (рис. 7).

67 Формирование математического мышления

Решение этой задачи стало очевидным.
В ходе решения задачи у некоторых школьников проявилось
стремление к рационализации решения: они обнаружили возможность
выполнять решение непосредственно на данном изображении
угла, а не строить угол, конгруэнтный данному, для осуществления
решения задачи. Кроме того, учащиеся в ходе реализации плана
решения обнаружили возможность произвольного выбора точки А
на окружности. Интересно отметить, что нескольким учащимся
‘найденный ими способ решения позволил усмотреть, что с его помощью
может быть решена и другая задача, аналогичная данной
(построить угол, величина которого двое больше величины данного
угла и т. д.).
Заботясь о целенаправленном развитии мышления учащихся в
процессе решения геометрических задач, учитель должен знать особенности
того или иного этапа решения учебной задачи (знать, какие
мыслительные умения школьников проявляются и формируются
на том или ином этапе решения задачи), оценивать значимость
каждого этапа для формирования математического развития школьников.
В методике принято деление процесса решения задачи на четыре
основных этапа.
~На первом этапе процесса решения математической задачи имеют
место осознание условия и требования задачи, усвоение и разработка
отдельных элементов условия (или элементов цели), поиск
необходимой информации в сложной системе памяти, соотнесение
условия и заключения задачи с имеющимися знаниями и
опытом.
На втором этапе имеют место целенаправленные пробы различных
сочетаний из данных и искомых, попытки подвести задачу под
известный тип, выбор наиболее приемлемого в данных условиях
метода решения (из известных): выбор стратегии решения, поиск
плана решения и его корректировка на основе предварительной
проверки, соотнесения с условием задачи и интуитивных соображений,
фиксирование определенного плана решения задачи.
На третьем этапе проводится практическая реализация плана
решения во всех его деталях с одновременной его корректировкой
через соотнесение с условием и выбранным базисом, выбор способа
оформления решения и оформление решения, запись результата.
На четвертом этапе фиксируется конечный результат решения,
проводится критический анализ результата (его прикидка и проверка),
осуществляется поиск путей рационализации решения, исследование
особых и частных случаев, выявление существенного —
потенциально полезного, систематизация новых знаний и опыта.
Изучение опыта работы учителей математики показывает, что
в практике обучения математике не уделяется должного внимания
первому этапу процесса решения задачи, второй этап решения задачи
не занимает должного места, третьему этапу уделяется излишнее
внимание, а четвертый, как правило, отсутствует.

68 Формирование математического мышления

Эффективное формирование математического развития школьников
возможно лишь при условии, что работа учащихся над решением
задач методически продумана, а на ее проведение отводится
достаточное учебное время. В этом случае сам процесс решения задачи
выступает не только как важнейшее из средств обучения математике,
но и как средство целенаправленного развития мышления
школьников.
В ходе внеклассных занятий возможна постановка особых проблемных
задач, построенных на известном учащимся учебном материале
и направленных либо на расширение имеющихся у школьников
знаний и опыта, либо на его углубление. Как правило, решение
таких проблемных задач переходит в изучение учащимися определенного
раздела математики, примыкающего к школьному курсу,
или в дополнительные самостоятельные исследования вопросов,
сгруппированных около поставленной и решенной проблемной задачи.
На кружковых и факультативных занятиях, помимо*задач проблемного
характера, полезна постановка задач, возбуждающих у
учащихся интерес к решению задач (а через него.— к изучению геометрии)
и одновременно реализующих те или иные развивающие
функции. Так, полезна постановка задач, способствующих развитию
конструкторских способностей и пространственного воображения.
Последнее следует формировать уже на материале курса планиметрии.
Вот пример родной из таких задач: «Квадрат разделен на 16 конгруэнтных
квадратов. Разделить его на две равновеликие фигуры,
проводя линию деления лишь по контуру квадратов, составляющих
данный».
Опыт показывает, что разнообразные способы решения этой
задачи вызывают у учащихся большой интерес (на рис. 8 показаны
решения этой задачи).
Полезна- также постановка задач, требующих обоснования невозможности
их решения при заданных условиях. Такие задачи
развивают критичность мышления школьников, способствуют формированию
их логичной культуры. Такова, например, следующая задача:
«Доказать, что круг нельзя покрыть двумя кругами меньшего,
диаметра».
В ходе решения этой задачи учащиеся должны провести следующие
рассуждения. Пусть меньший круг накрыбает часть большего.
Их центры принадлежат одной прямой 0г 02 . Если [АВ] — диаметр
большего круга, перпендикулярный к (0i02), то точки А и В нз

69 Формирование математического мышления

покрыты меньшим кругом. Так как расстояние между ними больше
диаметра другого меньшего круга, то хотя бы одна из них останется
непокрытой ни первым, ни вторым кругом. Опыт показывает, что
на кружковых и факультативных занятиях особенно полезны
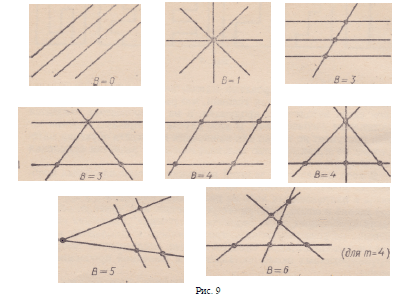
задачи поискового характера. Вот одна из таких задач: «Сколько
точек пересечения могут иметь четыре несовпадающие прямые плоскости?
Проиллюстрировать каждый из возможных случаев. Обосновать
невозможность того или иного случая.»
В ходе решения этой задачи у учащихся возникла идея о том,
что интересно было бы выяснить возможное число точек пересечения
другого числа несовпадающих прямых плоскости.
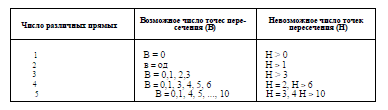
Решение поставленной задачи (рис. 9) переросло в целое исследование,
результаты которого были оформлены в виде следующей
таблицы:

70 Формирование математического мышления.

Далее перед учащимися была поставлена новая задача: «Найти
максимальное число точек пересечения различного числа несовпадающих
прямых плоскости».
Решение этой задачи также оформлялось в виде таблицы:

Внимание учащихся было обращено на то, что найденная последовательность
чисел обладает* определенными свойствами, что члены
этой последовательности могут быть записаны так:

Теперь учащиеся без труда установили общий член этой последовательности
и получили решение задачи для общего
случая.
Эта (и ей аналогичные) геометрическая ситуация может быть
использована для проведения проверочных работ, целью которых
является не только проверка усвоения определенных знаний и умений,
но и выявление того, как продвигаются учащиеся в своем
математическом развитии. При проведении таких работ важно подобрать
задачи, решение которых не требует знаний, выходящих
за рамки программного материала, но вместе с тем содержит изюминку,
заставляет школьников проявить определенные способности.
Таковы, например, следующие задачи:
1. Изобразить возможные случаи пересечения пяти прямых в четырех
точках.
2. Даны две окружности. Какими преобразованиями можно отобразить
одну окружность на другую? Проведите эти преобразования.
Рассмотрите возможные случаи.

71 Формирование математического мышления

Формирование математического мышления