Векторы

Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.

В. А. Гусев, Ю. М. Колягин, Г. Л. Луканкин, Д. И. Хан

 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ.
§ 1. Векторы

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

В. А. Гусев, Ю. М. Колягин, Г. Л. Луканкин, Д. И. Хан
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ.
§ 1. Векторы.

1. О трактовке понятия вектора
В соответствии с требованиями новой программы по математике
понятие вектора стало одним из ведущих понятий школьного курса
математики.
Действительно, понятие вектора тесно связано с принятой
сейчас теоретико-множественной трактовкой основных понятий
школьного курса математики. Например, с таким важнейшим понятием
школьного курса геометрии, как понятие перемещения. Кроме
того, понятие вектора находит достаточно, широкие приложения
при рассмотрении различных вопросов школьных курсов математики
и физики.
Уже на уроках физики в 8 классе изложение материала ведется
с широким привлечением векторного аппарата. Понятно, что это
заставляет задуматься прежде всего наа, тем, как наиболее естественно
ввести в курс математики восьмилетней школы понятие вектора,
как эффективнее применять это понятие при изложении
теории и решении задач, как рассматривать основные действия над
векторами.
Известно, что существует несколько подходов к введению этого
понятия.
В физике при помощи вектора изображаются различные направленные
величины: сила, скорость, ускорение и т. п., в силу чего
вектор обычно определялся здесь как направленный отрезок. При
этом часто такая направленная величина оказывалась существенно
связанной с определенной точкой (точкой ее приложения) или
прямой.
В математике же обычно имеют дело с так называемым свободным
вектором (вектором, не связанным ни с какой прямой и ни с
какой фиксированной точкой).

128 Векторы.

В традиционных математических курсах вектор также определялся
как направленный отрезок. При этом два вектора считались
равными, если они имели одну и ту же длину и направление. Однако
такое определение равенства векторов не вполне корректно,
так как тем самым отождествляются два хотя и родственные, но различные
понятия: «равенство» и «эквивалентность». Между тем
равенство математических объектов трактуется сейчас как их совпадение,
а эквивалентность — как любое отношение, обладающее
свойствами рефлексивности, симметричности и транзитивности.
Это различие четко реализовано сейчас в школьном курсе математики
(например, в понятиях конгруэнтности фигур и равенства).
Далее, равные сонаправленные отрезки принимались за представителей
одного так называемого свободного вектора, который,
таким образом, трактовался как бесконечное множество равных,
одинаково направленных отрезков. Каждая точка плоскости при
этой трактовке представляет собой начало некоторого отрезка из
семейства отрезков на плоскости. Эти отрезки затем разбиваются
на подмножества, в каждое из которых попадают лишь те, которые
одинаково направлены и равны по длине. Тем самым осуществляется
идея разбиения всех направленных отрезков плоскости на классы
эквивалентности, при этом каждый направленный отрезок является
«полномочным представителем» своего класса. Направленные
отрезки одного класса рассматриваются как представители
одного и того же свободного вектора.
Анализируя понятие вектора, нетрудно обнаружить, что с геометрической
точки зрения вектор — это объект, характеризуемый
направлением (т. е. некоторым множеством сонаправленных лучей)
и длиной. Однако, как известно, теми же самыми признаками характеризуется
и параллельный перенос (см.: К о л м о г о р
о в а . Н. и др. Геометрия, VI класс. 8-е изд. М., Просвещение,
1978, с. 80). Поэтому представляется наиболее естественным
всякий параллельный перенос назвать вектором (см.: Геометрия,
VII класс. 7-е изд. М., Просвещение,
1978, с. 59).
Такой подход к введению понятия вектора
не только логически безупречен, но и обладает
целым рядом достоинств методического
характера. Согласно прежнему определению
вектора два направленных отрезка, изображенных
на рисунке 1, считались равными
векторами. Однако мы не можем в этом случае
говорить о равенстве этих отрезков, так ка!
речь идет о разных множествах точек. Не ус
троил бы нас и термин «конгруэнтность», та!
как в этом случае оказались бы конгруэнтны
ми не только те два отрезка, которые наг.
нужны, но и, например, отрезки, изображен
ные на рисунке 2. Таким образом, возникают

129 Векторы.

трудности: разные множества (с теоретико-множественной точки
зрения) представляют один и тот же вектор.
Новое определение вектора не связано с понятием направленного
отрезка. Под вектором понимают либо множество упорядоченных
пар точек, задающих некоторый параллельный перенос, либо
сам этот перенос. В школьном курсе геометрии параллельным переносом
(вектором) называется отображение плоскости на себя,
при котором все точки плоскости отображаются в одном и том же
направлении на одно и то же расстояние. Такой подход к определению
вектора как параллельного переноса позволяет устранить
противоречия с теоретико-множественной точкой зрения на понятие
равенства, которое возникало при традиционном определении
вектора как направленного отрезка. Известно, что параллельный
перенос задается парой точек. В школьных учебниках различают
термины «две точки» и «пара точек»; в случае пары точек одна —
первая, а другая — вторая. Мы не пользуемся словами «упорядоченная
пара». Рассмотрим множество всех пар точек плоскости.
Для элементов рассматриваемого множества введем следующее
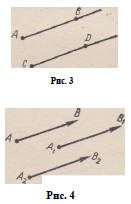
отношение: пары (А, В) и (С, D) будем называть эквивалентными
и обозначать (Л, В) — (С, D), если \АВ) 14 [CD) и \АВ\ — |CZ)|
(рис. 3). Это те пары точек, которые задают один и тот же параллельный
перенос. Эквивалентными между собой будем считать и
пары, у которых первая точка совпадает со второй. Легко проверить,
что такое отношение есть отношение эквивалентности, так
как обладает следующими свойствами:
1) рефлексивности: (Л, В) — (АВ);
2) симметричности: если (Л, В) — (CD), то (CD) — (А, В)\
3) транзитивности: если (Л, В) — (С, D) и (CD) — (К, М), то
(Л, J5) — (/С, М).
С помощью рассмотренного отношения эквивалентности производится
разбиение множества пар точек плоскости на непересека-
ющиеся подмножества (классы), элементами
которых являются эквивалентные
пары. Каждое из таких подмножеств
можно назвать вектором. Следовательно,
один и тот же параллельный перенос Т
(вектор) можно задать при помощи бесконечного
множества эквивалентных
между собой пар точек (Л, В)~(ЛЬ 5Х)~
~ (Л2, Я2) … (рис. 4), т. е. Т — ТА в =
Г/ —* — • • • •
Поэтому естественно говорить, что
направленные отрезки АВ, AiB v А2В2, •••
изображают один и тот же вектор а—
АВ= AX BX “ Л2$2 ••• •
Так как всякий класс (подмножество)
эквивалентных пар определяется любым

130 Векторы.

его представителем — любой его парой, то тем самым всякая
пара точек плоскости задает (определяет) некоторый вектор
на плоскости. При этом эквивалентные пары определяют один
и тот же вектор, а неэквивалентные пары — различные векторы.
Если вектор задается парой {А, В) (А Ф В), то его обозначают
АВ. Направление, определяемое лучом АВ, называют направлением
вектора А В, а расстояние \АВ \ — его длиной. Вектор,
длина которого равна единице, называется единичным вектором.
Пусть теперь вектор задается парой (В, В), т. е. парой, у которой
первая точка совпадает со второй; такой вектор ВВ называется
нулевым вектором и обозначается ВВ — 0. Длина нулевого вектора
равна нулю, т. е. | В В | = 101 = 0, а направление его не опреде-
лено. Итак, любой вектор а плоскости полностью определяется
заданием одной пары точек Л и В, где В = а (А). Заметим, что
направленный отрезок А В выступает при такой трактовке вектора
лишь как удобное наглядное изображение вектора. Любой вектор
а Ф 0 имеет бесконечное множество изображений в виде направленных
отрезков.
Итак, мы рассмотрели возможность введения понятия вектора
как множества пар точек, задающих один и тот же параллельный
перенос, т. е. множество всех пар (X, У), для которых Т (X) =** Y
есть вектор. Это множество пар (X, Y) иногда называют графиком
параллельного переноса.
В современной трактовке принято отождествлять график с самим
отображением. Все сказанное и привело к отождествлению
в школьном курсе математики параллельного переноса и вектора
как синонимов, обозначающих одно и то же понятие.
Понятие вектора, трактуемого как параллельный перенос,
включается в систему тех понятий, с которыми учащиеся знакомятся
в курсе геометрии 6 класса, а затем получает дальнейшее
развитие в курсе геометрии старших классов. Так, в учебном пособии
по геометрии для 9 класса под редакцией 3. А. Скопеца параллельным
переносом, определяемым парой (А, В) несовпадающих
точек, называется преобразование пространства, при котором
каждая точка М отображается на такую точку М1 9 что луч А1М1
сонаправлен с лучом АВ и расстояние \ММХ \ равно расстоянию
| АВ |. Таким образом, вектор определяется как множество пар точек,
задающих один и тот же перенос (т. е. также по существу понятия
вектора и параллельного переноса отождествляются).
Такая трактовка вектора значительно упрощает логическую
схему изложения курса геометрии. Так, например, операция сложения
векторов трактуется при этом как композиция параллельных
переносов. Кроме того, эта трактовка понятия вектора дает
возможность, определив само понятие вектора и операции над векторами
на плоскости, распространить эти определения и на случай

131 Векторы.

рассматривать
все вопросы одновременно для плоскости и пространства,
при необходимости оговаривая те случаи, когда то или иное
положение будет относиться лишь к векторам на плоскости или в
пространстве. Так как вектор трактуется как параллельный перенос,
то все известное учащимся о параллельном переносе распространяется
и на него. Таким образом, в курсе геометрии 6—8 классов
параллельный перенос (или вектор) рассматривают уже как
отображение всей плоскости на себя (а не какого-либо ее подмножества).
Векторы обозначают латинскими буквами со стрелкой наверху:
а, Ьу с и т. д.
Мы говорили уже о том, что вектор можно задать одной из эквивалентных
пар точек и что запись одного и того же вектора может
быть различной. Так, вектор, изображенный на рисунке 4,
можно записать так: А В = А1 В1 = А2 В2 .
Напомним, что в записи а = АВ = CD речь идет о различных
направленных отрезках АВ и CD, изображающих один и тот же
вектор а, но не о равенстве (или конгруэнтности) этих векторов.
— > ->
Вектор а Ф 0 можно задать, во-первых, указанием расстояния
—> О -*
(г > 0) и направления; во-вторых, соотношением X -*■ Х1 = а (X), —>
т. е. парой точек X и а {X).
Для дальнейшего важен случай, когда параллельный перенос
осуществлен на нулевое расстояние, т. е. имеет место тождественное
отображение Е (X) плоскости (или пространства). Такой параллельный
перенос называется нулевым вектором и обозначается
0. Для нулевого вектора также можно использовать различные
обозначения: АА = ВВ = XX.
Длина вектора выражается формулой \АВ\ = \АВ\.
Направление вектора есть общее направление лучей, представляющих
данный параллельный перенос. Для нулевого вектора направление
не определено.
Один из наиболее важных моментов, связанных с введением
понятия вектора, заключается в умении различать разные векторы
и видеть одинаковые векторы. Например, две точки А и В, где
А ф В, задают два вектора А В и В А.
Семь различных точек плоскости, из которых шесть точек —
вершины правильного шестиугольника, а седьмая — центр описанной
около него окружности, задают 19 различных векторов.
Важно также отчетливо понимать, что вектор есть отображение
точек всей плоскости (или пространства) на себя. Запись а (X) =
=: Хх следует читать так: вектор а отображает точку X плоскости

132 Векторы.

(или пространства) на точку Хх той же плоскости (или пространства).
В этой связи можно трактовать запись а — АВ = CD как
—► —►
запись отображений: В — а (Л), D = а (С), при этом ясно, что
[АВ) и [CD) сонаправлены, а \АВ\ = \CD\.

133 Векторы.
Школьная Математика.

Векторы