Операции над векторами
Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.
В. А. Гусев, Ю. М. Колягин, Г. Л. Луканкин, Д. И. Хан
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ.
§ 2. Операции над векторами
Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):
Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
В. А. Гусев, Ю. М. Колягин, Г. Л. Луканкин, Д. И. Хан
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ.
§ 2. Операции над векторами.
1. Сложение и вычитание векторов
—> —>
Суммой двух векторов а и b называется отображение плоскости
на себя, являющееся результатом последовательного выполнения
отображений а и b (т. е. композиция bod).
Сумма векторов может обозначаться так:
а +1 или (а + Т>) (X) = 6 (а {X)).
Отметим, что в методической литературе имеет место упрощение
терминологии. Например, говорится: построить вектор АВ =
= CD + EF, что означает: построить направленный отрезок,
изображающий вектор А В, который является суммой двух данных
векторов CD и EF. Мы также будем использовать подобные упрощения
в терминологии.
Известное правило треугольника, вытекающее из определения
.суммы векторов, позволяет геометрически
найти сумму данных векторов (рис. 5).
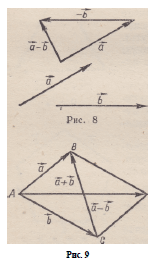
Интересен
случай, изображенный на рисунке 6.
Здесь сумма векторов оказалась нуль-векто-
ром. Этот случай ярко иллюстрирует отличие
смысла математического термина «перемещение
» от его житейского толкования (путь).
Если, найример, ситуацию, изображенную
на рисунке 6, истолковать как поведение путешественника
в незнакомом городе, который
долго -бродил по улицам и вернулся в гости- АВ+ВС=АС
ницу (им проделан значительный путь), то пе- Рис> 5
ремещение (результат пути) выражается нулевым
вектором. Путешественник «отобразился
» в исходную точку.
Рассмотрим физическую задачу, при решении
которой используется сложение векторов.
З а д а ч а . Лодка движется от одного бе-
—►
рега к другому со скоростью скорость те-
чения реки v2 . Какова истинная скррость движения
лодки?
Р е ш е н и е . Изобразим условия задачи
с помощью векторов (рис. 7). Тогда решением
задачи будет vH C T = vx + v2 .
133 Операции над векторами.
Так как любое перемещение F обратимо,
то F-1 также является перемещением,
причем F~1 oF=Fo F~X =E.
Если F = а, тогда по определению
F*1 = —а есть противоположный вектор,
а из утверждения F~x —► —► —► о F = Е
следует, что а + (—я) — 0.
Из определения суммы векторов по-
лучаем закон поглощения нулевого вектора: а + 0 =* 0 + а = а.
—> —>■ —>
Нетрудно установить, что из равенства с — а + (—Ь) следует
b + с — а. В самом деле, b [а + (—£)] = b -f [(—b) + а] =
—>• —>- —>• —V —► ■—>
= (6 + (—Ь)) + а = 0 + а = а. Здесь мы пользуемся законами
коммутативности и ассоциативности сложения векторов (см. п. 4).
—>О —тс>ю —да> е —сте>с —тве>н•н ым образом получаем определение разности
а — b как вектора с, такого, что 6 + с = а.
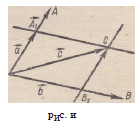
Геометрическое построение разности векторов представлено
—>•—>•^^*“■>*
на рисунке 8: а — Ь™= я + (—6),
Заметим, что операции сложения и вычитания векторов нередко
встречаются в жизненных ситуациях, на которые мы обычно не
обращаем внимания, например:
1) пешеход в безветренную дождливую погоду наклоняет зонтик
вперед, хотя дождь падает отвесно;
2) дождевые полосы на окнах вагона
двух встречных поездов имеют
различные направления.
Отметим, что разность и сумма
двух векторов могут изображаться направленными
диагоналями одного и
того же параллелограмма (рис. 9).
2. Умножение вектора на число.
Умножение вектора на число можно
определить так:
1) о • а = 0; 2) k • 0 = 0;
—>-*■ -►
3) если k > 0, а ф 0, то k • а есть
-»■ —»■
вектор направления а длины k\a\-,
4) если k < 0, а Ф 0, то k — а есть
вектор направления, противоположного
направлению а, длины \k\ • |а|.
Числовой множитель пишут слева.
Произведение вектора на число
можно определить и так, как это сдела-
но в учебном пособии по геометрии для
134 Операции над векторами.
7 класса (Геометрия, VII класс. М., Просвещение, 1978, с. 90): «Произ-
ведением вектора а на число х называется вектор, имеющий (при
а ф 0) направление вектора а, если х > 0, и противоположное
направление, если х < 0. Длина этого вектора равна произведению
длины вектора а на модуль числа х».
Заметим, что оговорка, сделанная в данном определении относительно
а (аф 0), необходима для указания направления вектора
х • а (в этом случае необходимо оговаривать и то, что х ф 0). Для
указания длины этого вектора такие оговорки не нужны.
Приняв это определение умножения вектора на число, необходимо
особо рассмотреть случаи умножения вектора на число 0 и
умножение нулевого вектора на любое число х.
Из определения следует, что \х • а\ = |*| • |а|. (1)
а) Пусть |лг| = 0, тогда правая часть равенства (1) есть нуль.
—> —► —> —у
Значит, | х • а\ — 0, т. е. 0 ■ а = 0 для любого а.
—>■ —>• “>->
б) Пусть а = 0, тогда |а| = |0| = 0, т. е. правая часть равенства
(1) также обращается в нуль для любого числа х. Значит,
—> —у —>
\х • а\ — 0, т. е. х • 0 = 0 (закон поглощения нулевого вектора).
Прежде чем рассматривать остальные свойства операции умножения
вектора на число, рассмотрим вопрос о коллинеарных векторах.
3. Коллинеарные векторы
Пусть О — любая точка плоскости. Каждый вектор а ф 0 имеет,
как известно, бесконечно много изображений в виде направленных
отрезков. Заметим, что легко осуществить операцию по построению
направленного отрезка ОК, для которого ОК — а. Действительно,
с этой целью достаточно через точку О провести луч
с началом в точке О, имеющий то же направление, что и вектор а,
«■>
а затем на этом луче отложить отрезок О К длины | а |. Операцию
построения направленного отрезка ОК, для которого ОК — а,
называют откладыванием вектора а от точки О.
Пусть на плоскости заданы сонаправленные или противополож-
но направленные векторы а, 6, с
(рис. 10). Каждый из этих векто- сГ
ров отложим от одной и той же —
точки О. Мы видим, что они изобра- _ Т
жаются направленными отрезками ^ ~ Г ^
одной и той же прямой. ^7″^’*
Векторы, которые могут быть 1ДД:_________ 6 и мгС „
изображены направленными отрез- в 0 с С А
ками одной и той же прямой, на- Рис. 10
135 Операции над векторами.
зываются коллинеарными. Таким образом, векторы а, b и с кол-
линеарны. Можно также сказать, что ненулевые векторы коллине-
арны, если их направления совпадают или противороложны.
—► ->
Заметим, что вектор а коллинеарен ненулевому вектору b тогда
и только тогда, когда существует такое число k ф 0, что выполняется
равенство а = kb. Нулевой вектор считается коллинеарным
любому вектору.
Используя операцию откладывания вектора от некоторой точки
О, всегда можно любые векторы, заданные на плоскости, привести
к этой точке (сделать ее началом направленных отрезков, изображающих
данные векторы).
В ряде случаев оказывается удобным рассматривать векторы
в некоторой системе координат.
Рассмотрим прямоугольную декартову систему координат хОу.
Отложив на лучах Ох и Оу отрезки единичной длины ОЕх и ОЕ.„
получим два вектора, которые принято обозначать:
ОЕх — i, ОЕу = /.
Мы видим, что система координат может быть определена ука-
занием точки О и единичных векторов i и /. Векторы i и j взаимно
перпендикулярны и имеют одинаковую длину. Значит, можно
считать, что произвольная прямоугольная декартова система координат
задается указанием начальной точки О и двух взаимно пер-
пендикулярных векторов i и / одинаковой длины. Неравные нулю
векторы а = ОА и Ъ = ОБ перпендикулярны, если угол между направлениями
этих векторов прямой. Нулевой вектор считают перпендикулярным
любому другому.
Существует взаимно-однозначное отображение а = ОА А
—>■
множества всех векторов а на множество всех точек А плоскости,
а также отображение А -> (х, у), т. е. множество всех точек А
плоскости на множество всех пар чисел (х, у). Возникающее отсюда
отображение а (х, у) тоже взаимно-однозначно. Поэтому числа х
— >
и у можно считать и координатами вектора а: они однозначно определяются
вектором айв свою очередь, взятые вместе, однозначно
определяют вектор а. Нетрудно усмотреть, что а = О А — х • i -f
+ у • /. Таким образом, вектор а может быть представлен в ви-
де а = х • i + у • / единственным образом.
—>
Координаты вектора а обозначаются ах и ау соответственно.
Мы исходили из определенной системы координат, заданной —> — У
точкой О и векторами i и /. Но нетрудно заметить, что коэффициен-
ты ах и ау представления а — ах • i -f ау • j не зависят от выбора
точки О.
136 Операции над векторами.
Векторы ах = ау ■ г, а • / называются составляющими вектора
а в данной системе координат.
Так как коллинеарные векторы могут быть изображены направленными
отрезками одной прямой, возникает возможность выражения
коллинеарных векторов через координаты точек прямой. Отсюда
можно найти условие, при котором направленные отрезки прямой
изображают один и тот же вектор.
Обозначим е — ОЕ Ф 0, где О — начальная точка (нулевая).
Тогда \ОЕ\ — е — единица длины. Так как каждая точка прямой
характеризуется своей абсциссой х а , хв и т. д., нетрудно установить
условие совпадения векторов на прямой:
АВ = CD<&(\ хв — хА | = \xD — хс\П (sign (хв — хА ) = sign (xD —
— хс )), т. е. АВ = CD <=> хв — х а — x d — х с .
Пусть, например,
х а — 2; хв = —4; хс — 7; Xd — 1; тогда АВ — CD, так как
—4 — 2 = 1 — 7; —6 = —6.
В векторном исчислении и его приложениях большое значение
имеет представление (разложение) вектора в виде суммы нескольких
векторов, называемых составляющими данного вектора. Разло-
жить вектор с по двум неколлинеарным векторам а и b — значит
представить его в виде суммы двух векторов, которые будут колли-
иеарны данным векторам а и Ь.
Пусть заданы три неколлинеарных вектора а, Ь, с. Разложим
— > —>■ —у *
вектор с по векторам а и Ь. Для того ч’т о-б>ы — >разложить вектор с по
двум векторам (неколлинеарным) а и Ь, надо представить с в виде
суммы двух векторов, коллинеарных соответственно а и Ь. Для
этого от точки О отложим векторы а, b и с (рис. 11).
Через точку С проведем прямые, параллельные отрезкам ОА и
ОВ. Получим параллелограмм, в котором [ОС] — диагональ.
В этом параллелограмме ОС = ОАг + ОВ1 У причем ОАх коллине- —> —»>■ —>
арен а, —ОВ ■г’ к>о л—ли>н е—ар >ен■ —Ь.> З■на чит, мож—но> н■а йти— та>к ие ч—ис>ла х и
у, что ОЛх = ха, ОВх = уЬ. А -тогда с — ха + уЬ, т. е. мы представили
с в виде суммы двух векторов
-х>а — и >y b, соответственно коллинеарных
а п Ь.
Докажем теперь единственность разложения
вектора с. Доказательство про- ~
ведем методом от противного.
Допустим, что вектор с можно разложить
двумя способами: с == ха + уb
137 Операции над векторами.
и с — xt a + yxb, где хфхъ у Фух . Так как
с — один и тот же вектор, то, применяя
свойства сложения векторов и умножения
вектора на число, имеем:
-*■ — > — > — > — > ■ — * ■ — * •
хх а + уф = ха + yb, хх а — xa — yb — уг Ь,
(хх — х) а = (у — у^ Ь, а — у~у* Ь.
Следовательно, а коллинеарен Ь. Получили
противоречие с условием. И потому
= * и yt = у.
Итак, установлено существование и единственность такого разложения.
В общем случае, когда а и b — произвольные неколлинеарные
векторы, заданные в определенном порядке (а — первый, b— вто- —у — > — — >
рой векторы (базиса)), а— с> ■— — >х а-> + yb, то числа хну называют ко-
ординатами вектора с относительно базиса (а, Ь).
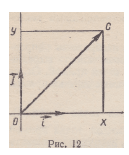
Разложение вектора с по двум перпендикулярным векторам,
или, другими словами, по направлениям координатных осей декартовой
прямоугольной системы координат хОу, заданной в плоскости
(рис. 12), является частным случаем рассмотренного выше
разложения.
Следовательно, и в этом случае ОС = xi + у/.
Векторы i и / называются базисными векторами; также говорят,
что они образуют координатный базис. Представление вектора с
в виде суммы (составляющих векторов) называется разложением
этого вектора по базису i и /. Коэффициенты х и у при базисных
векторах i и / называют д~еукартовыми координатами вектора с.
В дальнейшем вектор с, заданный координатами л: и у, будем обозначать
так: с = (х, у) и записывать: с = xi + yj. В этом случае
будем говорить, что вектор задан в координатной форме.
4. Свойства операций над векторами
Основные законы векторной алгебры представлены следующими
свойствами:
—У —У —> —У 1 )а+Ь=Ь + а — коммутативность;
—У. —У —У —У —У —У 2) a+(b-\-c)={a-\-b) + с— ассоциативность;
—У —У —У —У —У
3)а + 0 = 0 + а = а — закон поглощения нулевого вектора;
— У — у
4) (ху) • а — х (у • а) — сочетательность;
5) ха + у а = (л: + у) а — первый распределительный закон;
138 Операции над векторами.
6) ха + xb — х (а + b) — второй распределительный закон;
—> —У 7) 0 • а — О — закон поглощения нуля;
—> —У 8) х • 0 = 0 — закон поглощения нулевого вектора.
5. Скалярное произведение двух векторов и его свойства
В 6—8 классах скалярное произведение векторов не рассматривается,
однако для плоскости эта операция может быть рассмотрена
на факультативах.
Скалярным произведением двух ненулевых векторов называется
число, равное произведению числовых значений длин этих векторов
на косинус угла между векторами.
—> —> —У -> —У —У
Обозначение: а • b — \а\ • |Ь| • cos (а, Ь).
—у —> —>
П р и м е р . Пусть даны векторы а и Ь, длины которых | а\ = 2
и |6| = 3, угол между ними равен 60°. Тогда скалярное произведение
этих векторов будет равно:
а • b — | а | • | b [cos (а Ь) = 2-3 cos 60° = 2-3>— = 3.
2
Если из двух векторов хотя бы один вектор нулевой, то скалярное
произведение таких векторов принимается равным нулю.
Свойства скалярного произведения
—У—у—У—У * 1. а • b = b • а (коммутативность).
—У —У —>• —У —У —>■ —У 2. (а +b)»c = a*c+b>c (дистрибутивность).
—У —► —► —►
3. та • пЪ == (т • п) а • b, т. е. числовой множитель можно
выносить за знак скалярного произведения.
4. если а ± Ь, то cos (а, Ь) = 0 и а • 6 = 0. Скалярное произведение
перпендикулярных векторов равно нулю.
Из этого свойства вытекает справедливость следующей теоре-
мы: для того чтобы два ненулевых вектора а и b были перпендикулярны,
необходимо и достаточно, чтобы скалярное произведение
этих векторов было равно нулю, т. е. а • b — 0.
5. выражение а • а будем обозначать а2 и называть скалярным
—у квадратом вектора а. Скалярный квадрат вектора равен квадрату
—У —У
числового значения его длины, т. е. а2 — |а|* = а2.
6. косинус угла между ненулевыми векторами а и b равен скалярному
произведению этих векторов, деленному на произведение
числовых значений длин векторов, т. е.
/\ -У -У
cos (/~а,* о и)\ = а• Ь
м-m
6. Операции над векторами, заданными своими прямоугольными
координатами
139 Операции над векторами.
Как известно, любой вектор в пространстве можно разложить
по трем данным некомпланарным векторам. На практике чаще всего
в качестве тройки векторов используют упорядоченную тройку
(/, /, k) попарно ортогональных единичных векторов. Пусть разло-
жение вектора а по базису (i, /, k) имеет вид:
а = ах i -j~ c i y j -j- clJz .
Числа ax, ay 9 az называют координатами вектора а относитель-
но базиса (i, /, k). Так как в данном случае базис прямоугольный,
то они получили название прямоугольных (декартовых) координат.
Для обозначения используется краткая запись:
а = (ах’ ау- аг)’
Известно, что если вектор а задается парой (Л, В), где точки
Л и £ в прямоугольной (декартовой) системе координат заданы
своими координатами А (хх, ух, 2Х) и В (х2 , у2, г2), то вектор а = Л В
имеет следующие прямоугольные координаты:
Ux — ~ У2 Ул» ^ 2 = ^*2 ^1*
Например, направленный отрезок, изображающий вектор АВ,
имеет начало в точке А (3; 2; —1) и конец в точке В (4; —5; 3);
тогда координаты вектора АВ имеют вид: ах — 4 — 3 = + 1 ,
ау = -5 -_2 = -7, аг = + 3 — (-1) = +4.
Итак, АВ = (+1, —7, +4).
Свойства операций над векторами
Имеют место следующие теоремы об операциях над векторами,
заданными в координатной форме.
1. Пусть даны а = (ах , ay t az ) и b — (bx , by , bz ), тогда сумма
этих векторов есть вектор с, координаты которого равны сумме
— > — ► —>
одноименных координат слагаемых векторов, т. е. с = а + b —
== ^X» «у ^у> ^)*
П р и м е р , а = (3; 4; 6) и Ь = (—1; 4; —3), тогда
с = (3 + (-1); 4 + 4; 6 + (-3)) = (2; 8; 3;).
2. а — (ах , ау , аг ) и 6 = (6Х, Ьу, &*), тогда разность этих векторов
есть вектор с, координаты которого равны разности одно-
именных координат данных векторов, т. е. с — а — b = (ах — Ьх ,
ау — Ьу \ аг — bz ^
П р и м е р , а = (—2; 8; —3) и 6 = (—4; —5; 0), тогда
с = а —?==(—2 —(—4); 8 —(—5); —3 — 0) = (2; 13; —3).
140 Операции над векторами.
3. При умножении вектора а = (ах , ау , az ) на число т все его
координаты умножаются на это число, т. е.
та — (тах «, тау \ таг ).
П р и м е р , а = (—8; 4; 0) и т = 3, тогда
За = (-8-3; 4-3; 0-3) = (—24; 12;. 0).
4. Пусть а — (ах , ау , az ), b — (bx , by , Ьг ). Тогда скалярное
произведение этих векторов равно сумме произведений одноимен-
— > — > —
ных координат данных векторов, т. е. а • b = ах Ьх + ау Ьу +
+ az bz .
П р и м е р . Пусть а = (1; —5; 8) и b — (0; 3; —2), тогда
a -ft- 1-0+ (—5)-3 + 8-(—2) = — 31.
—> —>
5. Пусть вектор а задан координатами, т. е. а — (ах , ау , аг ).
Тогда числовое значение его длины |а| = V+ a l + «f, а
косинусы углов между направлениями вектора а и положительными
направлениями осей координат (т. е. ортами) вычисляются
по формулам
аХ ау
cos а = | -I* cos 6 = Ttq’ cos у = i -*.*
I а I 1 a I _ I a |
-+■
Эти косинусы называются направляющими косинусами вектора а.
П р и м е р. Найти числовое значение длины и направляющие
— >
косинусы вектора а = (—2; 3; —5).
Р е ш е н и е . Находим числовое значение длины вектора:
| а | = V а2
х + а2
у + a2
z = V(~2)2 + 34- (~5)2 = V38;
далее,
cos а = -т=—^2, cos р =о -т=г, 2c os у = -т=-. —5
Y 38 /38 ‘ Y 38
141 Операции над векторами.

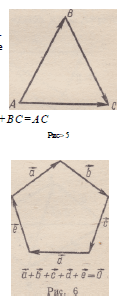


Свежие комментарии