Избранные в опросы теории преобразований подобия плоскости

З. А. Скопец, Л. И. Кузнецова

Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Приступая к рассмотрению вопросов теории преобразований подобия
плоскости, мы считаем известными следующие определения,
свойства плоскости и свойства перемещений плоскости:
1) Обратимое отображение плоскости на себя называется преобразованием
плоскости или геометрическим преобразованием.
2) Отображение плоскости на себя, при котором расстояние
между любыми двумя точками равно расстоянию между их образами/
называется перемещением плоскости*
3) А к с и о м а п о д в и ж н о с т и п л о с к о с т и . Если ^
расстояние \ А В \ положительно и равно расстоянию \А1В1\, то
существуют два и только два перемещения, при которых точка А
отображается на Аъ а точка В — на точку В±.
Если а — полуплоскость с границей ( А В ) > то она этими двумя
перемещениями отображается на две различные полуплоскости с
границей (ЛА). гШ
Пусть, например, заданы точки Л, В, Аъ В.ъ такие, что \ А1В1\==<
= |ЛВ|>0(рис. 1). Одно из перемещений, при которых точки А
и В отображаются на At и Вх соответственно, обозначим буквой f€
Тогда, пользуясь аксиомой, нетрудно установить, что второе .перемещение
есть композиция Sa о Д где а — (Л^),
4) Исходя из аксиомы подвижности плоскости,
можно доказать, что существует
бесконечное множество перекещений и
каждое из них представимо композицией
— осевых симметрий, причем число осевых
симметрий в композиции не более трех.

Перемещение, равное композиции двух осевых симметрий, называется перемеще-

183 Избранные в опросы теории преобразований подобия плоскости.

кием первого рода. Осевая симметрия и
перемещение, равное композиции трех
осевых симметрий, но отличное от осевой
симметрии, называются перемещением второго
рода.
Перемещения первого и второго рода
можно классифицировать далее по числу
неподвижных точек.

О п р е д е л е н и е . Точка А называется неподвижной точкой
преобразования /, если f (А) = А.
При классификации перемещений по роду и числу неподвижных
точек обнаружим пять и только пять видов перемещений плоскости.
Из них три вида перемещений первого рода (тождественное преобразование,
поворот вокруг точки и параллельный перенос) и два
вида перемещений второго рода (осевая симметрия и переносная
симметрия).
Если же классифицировать перемещения по роду и числу неподвижных
точек и двойных прямых, то центральная симметрия
также выделяется как самостоятельное перемещение.
З а м е ч а н и е . Прямая а называется двойной прямой преобразования
/, если / (а) = а. Если каждая точка прямой а отображается
на себя (неподвижна), то прямая а называется неподвижной.
Двойные и неподвижные прямые — инвариантные фигуры преобразования.
5) С понятием преобразования неразрывно связаны понятия
направления на плоскости и ориентации плоскости.
Если два луча параллельны, то один из них отображается на
другой либо центральной симметрией, либо композицией двух
центральных симметрий.
Луч л:2 называется сонаправленным с лучом хъ если существует
композиция двух центральных симметрий, при которой луч хг
отображается на луч х2-
Луч *2 называется противоположно направленным с лучом х19
если существует центральная симметрия, отображающая луч хг
на луч х2.
Отношение сонаправленности на множестве лучей, параллельных
данному лучу, есть отношение эквивалентности. Класс эквивалентности
по отношению сонаправленности на множестве лучей,
параллельных данному лучу, называется направлением на плоскости.
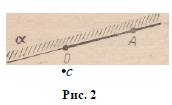
О п р е д е л е н и е . Объединение полуплоскости и луча на
ее границе называется плоским репером.
Репер, заданный полуплоскостью а и лучом ОА на ее границе*
обозначается ([ОА), а) или (О, Л, В), где А — точка открытого луча
О А, В — точка открытой полуплоскости а (рис. 2).
Пользуясь аксиомой подв-ижности плоскости, нетрудно доказать,
что один плоский репер отображается на другой либо осевой
симметрией, либо композицией двух осевых симметрий, либо композицией
трех осевых симметрий, не равной осевой симметрии.

184  Избранные в опросы теории преобразований подобия плоскости.

Репер х2 называется соориентирован- Р
ным с репером хъ если существует композиция
двух осевых симметрий, отображающая
репер хх на репер л;2.
Репер х2 называется противоположно
ориентированным реперу хъ если существует
осевая симметрия или композиция
трех осевых симметрий, отображающая
репер хг на репер х2.
Отношение соориентированности реперов
есть отношение эквивалентности на
множестве плоских реперов. Это отношение
имеет два и только два класса эквивалентности.

Класс эквивалентности по отношению соориентированности
на множестве плоских реперов называется ориентацией плоскости.
Репер, определяющий выбранную ориентацию, называется положительно
ориентированным. Тогда репер, принадлежащий другому
классу эквивалентности, называется отрицательно ориентированным.
*
По традиции, исходя из наглядных представлений, положительно
ориентированным принято считать такой репер (О, А, В)у
у которого «обход» точек О — А — В по сторонам треугольника ОАВ
совершается против хода стрелки часов (рис. 2). Репер (О, Л, С)
на рисунке 2 отрицательно ориентирован.
Так как любое перемещение первого рода представимо композицией
двух осевых симметрий, то^оно не меняет ориентации репера,
а значит, и ориентации плоскости. Перемещение второго рода
представимо композицией трех осевых симметрий и, следовательно,
меняет ориентацию репера, а значит, и ориентацию плоскости.
6) Угол АОВ называется ориентированным и обозначается
/-АОВ, если стороны его упорядочены (ЮЛ) — первая сторона,
[05) — вторая).
Всякий ориентированный угол АОВ определяет плоский репер
(О, А, В). Если этот репер положительно ориентирован, то и угол
АОВ положительно ориентирован. Если же репер (О, Л, В) отрицательно
ориентирован, то и угол АОВ отрицательно ориентирован.
Мера положительно ориентированного угла считается положительной,
отрицательно ориентированного — отрицательной.
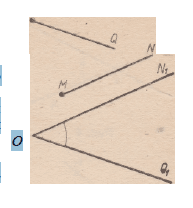
Углом между двумя лучами, заданными в определенном порядке,
называется мера ориентированного угла, стороны которого соответственно
сонаправлены с данными лучами. Например, углом
между лучами MN и PQ (рис. 3) является мера угла N±OQv Обозна-
чение: ([MNJT.[PQ)) = N^Sqv

185 Избранные в опросы теории преобразований подобия плоскости.

7) Углом между двумя пересекающимися
прямыми, заданными в определенном
порядке, называется мера, не превосходящая
по абсолютной величине 90°, ориентированного
угла, первая сторона которого
лежит на первой прямой, вторая — на
второй.
Например, углом между прямыми а и b
на рисунке 4 является мера угла АОВ.
Обозначение угла между двумя прямыми,
заданными в определенном порядке, —(а, b):
(а, b) = АОВ, ф, а) = ВО А.
Ясно, что (а, b) — —(b, а).
Угол между параллельными прямыми
считается равным нулю.

186 Избранные в опросы теории преобразований подобия плоскости.

Похожие статьи:
Школьная Математика. Школьный курс математики. Школьная математика скачать. Школьные учебники по математике.
Школьные задачи по математике. Математика 1 класс. Математика 2 КЛАСС. Математика 3 КЛАСС. 

Подобия плоскости