Дачный участок

Дачный участок.

Текст просто для быстрого ознакомления с темой в общих чертах (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):

ЗАДАЧА
При постройке дачи нужно было отгородить дач-
ный участок. Материала имелось на / погонных
метров изгороди. Кроме того, можно было воспользо-
ваться ранее построенным забором (в качестве од-
ной из сторон участка). Как при этих условиях
отгородить прямоугольный участок наибольшей пло-
щади?
РЕШЕНИЕ
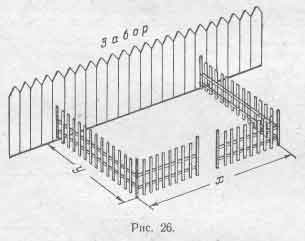
Пусть длина участка (по забору) равна х, а ши-
рина (т. е. размер участка в направлении, перпенди-
кулярном к забору) равна у (рис. 26). Тогда для

Дачный участок

огораживания этого участка нужно х+2у метров из-
городи, так что
Площадь участка равна
S=xy=y{l—2y).
Она принимает наибольшее значение одновременно
с величиной
2уA-2у)

163 Дачный участок 

(удвоенной площадью), которая представляет собой
произведение двух множителей с постоянной суммой /.
Поэтому для достижения наибольшей площади
должно быть
О/7-/ 9/7
откуда
1 1 О 1
4 2
Иначе говоря, х = 2у, т. е. длина участка должна
быть вдвое больше его ширины.

Желоб наибольшего сечения

ЗАДАЧА
Прямоугольный металлический лист (рис. 27) на-
до согнуть желобом с сечением в форме равнобокой
трапеции. Это можно сделать различными способами,

как видно из рис. 28. Какой ширины должны быть
боковые полосы и под каким углом они должны быть
отогнуты, чтобы сечение желоба имело наибольшую
площадь (рис. 29)?
РЕШЕНИЕ
Пусть ширина листа /. Ширину отгибаемых боко-
вых полос обозначим через Л’, а ширину дна желоба—

164 Дачный участок 

через у. Введем еще одно неизвестное г. значение
которого ясно из рис. 30.
Площадь трапеции, представляющей сечение же-
лоба,
Задача свелась к определению тех значений х, у, г,
при которых 5 достигает наибольшей величины; при
этом сумма 2х+у (т. е. ширина листа) сохраняет
постоянную величину /. Делаем преобразования:
S2=(y+z)*{x+z)(x—z).
Величина S2 становится наибольшей при тех же
значениях х, у, г, что и 352, последнюю же можно
представить в виде произведения
Сумма этих четырех множителей
y+z+y+z+x+z+3x—3z=2y+4x=2l,
т. е. неизменна. Поэтому произведение наших четы-
рех множителей максимально, когда они равны между
собой, т. е.
y+z—x+z и x+z=2>x—З2
Из первого уравнения имеем:
У=х,
а так как у + 2х=1, то х = у = -^
Из второго уравнения находим:
х_ l_
Z~ 2 ~ 6 »
Далее, так как катет z равен половине гипотену-
зы х (рис. 30), то противолежащий этому катету угол
равен 30°, а угол наклона боков желоба ко дну равен
90°+30° =120°.
Итак, желоб будет иметь наибольшее сечение,
когда грани его согнуты в форме трех смежных сто-
рон правильного шестиугольника.

165 Дачный участок

Школьная математика.

Околоadmin