Две окружности пересекаются
Избранные в опросы теории преобразований подобия плоскости.
Две окружности пересекаются. § 6. Общие пары соответственных точек двух преобразований (часть 4).
З. А. Скопец, Л. И. Кузнецова
Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.
Избранные в опросы теории преобразований подобия плоскости.
З. А. Скопец, Л. И. Кузнецова
Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):
Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Две окружности пересекаются. § 6. Общие пары соответственных точек двух преобразований. (часть 4).
6. Связь подобия первого рода с двумя
пересекающимися окружностями.
Пользуясь теоремами 1 и 2, доказанными
в § 5, легко установить следующий факт.
Если даны две пересекающиеся окружно-
218 Две окружности пересекаются.
сти, то одну из точек пересечения можно принять за центр преобразования
подобия первого рода, отображающего одну окружность на
другую. Тогда прямые, проходящие через вторую точку, пересекают
данные окружности в парах соответственных при этом подобии
точек.
З а д а ч а 1 0 . Окружности с о и с о х пересекаются в двух точках.
Прямая, проходящая через одну из точек пересечения, пересекает
окружности вторично в точках А и Ах. Доказать, что величина
угла между касательными, проведенными к окружностям в точках А
и Ах соответственно, не зависит от выбора секущей.
Р е ш е н и е . Пусть со П сог = {S; М} (рис. 49). Рассмотрим
преобразование подобия первого рода с центром S, отображающее
со на щ. Тогда любая прямая а, проходящая через точку М, пересекает
окружности в парах соответственных точек А и Ах. Касательная,
проведенная к окружности сох в точке Лг, есть образ
касательной, проведенной к окружности со в точке А. Но угол
между лучом и его образом при подобии первого рода — величина
постоянная. В данном случае она равна O S O x , где О и О х — центры
окружностей со и сох. Следовательно, угол между касательными
равен OSOx или 180° — OSOx.
З а д а ч а 1 1 . Даны два одинаково ориентированных квадрата
О А В С и О А х В х С х . Доказать, что прямые А А Х , В В Х и ССХ пересекаются
в одной точке.
Р е ш е н и е . Так как квадраты ОАВС и О А х В х С х одинаково
ориентированы, то существует преобразование подобия первого
рода, отображающее квадрат О А В С на квадрат ОЛ^С^ При этом
окружность, описанная около квадрата ОАВС, отображается на
окружность, описанную около квадрата ОАхВхСх (рис. 50). Центр
О подобия совпадает с одной из точек пересечения окружностей.
Тогда прямые, проходящие через пары соответственных точек
Л и Ах, В и Въ С и Сх, проходят через вторую точку пересечения
окружностей. Если квадраты ОАВС и ОЛ1В1С1 гомотетичны, то
окружности касаются и искомая точка совпадает с точкой О.
219 Две окружности пересекаются.
З а д а ч а 1 2 . Даны две различные точки А и В. Точка М принадлежит
прямой АВ. На отрезках AM иМВ построены квадраты
в одной полуплоскости с границей ( А В ) . Около квадратов описаны
окружности, пересекающиеся вторично в точке N. Найти множество
точек N при различном выборе точек М на прямой АВ.
Р е ш е н и е . Точка М либо принадлежит отрезку АВ, либо
не принадлежит ему. Рассмотрим каждый из этих случаев.
1) а) Пусть -М $ [ А В ] , A M C D и M B P Q — квадраты,около
которых описаны окружности со и <»х> о П — {М, N } (рис. 51).
Любая из точек М н N может быть принята за центр преобразования
подобия первого рода, отображающего окружность со на сох-
Рассмотрим преобразование Пд,. При нем А-+В, М — + Р , С -+Q,
D -»■ М, т. е. ( A M ) -> ( В Р ) . Так как по условию прямые A M и
В Р перпендикулярны, то угол поворота рассматриваемого подобия
равен 90° и A N B = 90°. Значит, точка N принадлежит окружности
6 с диаметром А В .
б) Пусть N x € б. Тогда A N X B = 90°. Построим на отрезке А В
точку М х так, что | А М Х \: | МхВ|= | A N X|: | |. Квадрат A M ^ D ^
отображается на квадрат BPxQi^i при преобразовании подобия
с центром N l t углом 90° и коэффициентом k =| M V B \ : \ М х А \ .
Значит, окружности, описанные около этих квадратов, пройдут
через точку N x — центр преобразования подобия.
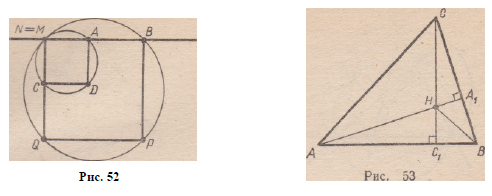
2) Если М £ ( А В ) , н о М i [ А В ] , то окружности о и сох касаются,
т. е. N — М (рис. 52).
Таким образом, искомое множество точек есть объединение
окружности с диаметром А В и дополнения отрезка А В до прямой,
исключая точки А и В .
7. Два преобразования подобия первого рода с общим центром.
Пусть при преобразовании подобия первого рода с центром М
точки А и С отображаются на точки В и D соответственно, тогда
M B = C M D и \ M B \ — . \ M A \ — |АШ|:|Л1С|,
220 Две окружности пересекаются.
Ш С = В Ш ) = ф и \ М С \ : \ М А \ = | M D | : | M S | = k .
Но они означают, что точки С и D есть образы точек А и В
соответственно при композиции поворота Rm и гомотетии Н м ,
т. е. при преобразовании подобия первого рода с центром М, углом
поворота ф и коэффициентом k .
Покажем применение этого свойства при решении задач.
З а д а ч а 1 3 . Доказать, что прямые, содержащие высоты
треугольника, пересекаются в одной точке.
Р е ш е н и е . Дан треугольник A B C , ( А А г ) и (ССХ) — п р я мые,
содержащие его высоты, ( А А г ) f] ( C C i ) — Н (рис. 53).
Треугольники С Н А г и А В А г подобны (по двум углам) и одинаково
ориентированы. Поэтому существует преобразование подобия
первого рода, при котором А г -»- А г , Н -> В , С А. Тогда
существует и преобразование подобия, при котором А1-^А1, С,
В -»> А. При этом подобии лучи АгН и //В отображаются на лучи
АгС и С А соответственно. Но прямые АгН и АХС перпендикулярны.
Значит, и прямые НВ и С А перпендикулярны, т. е.
третья высота треугольника проходит через точку Я.
З а д а ч а 1 4 . На плоскости даны четыре прямые, пересекающиеся
попарно в шести различных точках.Доказать, что четыре
окружности, каждая из которых проходит через три из получен-
пых точек, пересекаются в одной точке.
Р е ш е н и е . Пусть А, В, С, D, М и N — точки пересечения
данных прямых (рис. 54). Существует единственное преобразование
подобия первого рода, при котором точки А и В отображаются
соответственно на точки D и^; центр О этого подобия есть вторая
точка пересечения окружностей ABN и DCN. Имеем: О -> О,
A — + D , В *->• С . Тогда существует и преобразование подобия
первого рода, при котором О -> О , А -*■ В , D -> С. Центр О этого
преобразования есть вторая точка пересечения окружностей A D M
и В С М . Таким образом, все четыре окружности проходят через
центр О рассматриваемых преобразований подобия.
221 Две окружности пересекаются.