Где устроить полустанок?

Где устроить полустанок?

УРАВНЕНИЯ  ВТОРОЙ  СТЕПЕНИ

Текст просто для быстрого ознакомления с темой в общих чертах (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):

Где устроить полустанок?
ЗАДАЧА
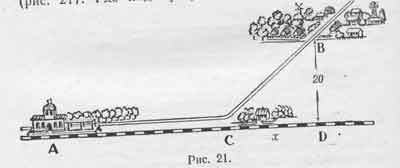
В стороне от прямолинейного участка железнодо-
рожного пути, в 20 км от него, лежит селение В
(рис. 21). Где надо устроить полустанок С, чтобы

Где устроить полустанок?

проезд от Л до В по железной дороге АС и по шоссе
СВ отнимал возможно меньше времени? Скорость
движения по железной дороге

150  Где устроить полустанок? 

РЕШЕНИЕ
Обозначим расстояние AD (от А до основания
перпендикуляра BD к AD) через a, CD через х. То-
гда ЛС=Л?>—CD=a—х, а С? =/С?>2 + В?>2 =
= у0с2-|-202. Время, в течение которого поезд прохо-
дит путь АС, равно
АС _ а — х
0,8 ~ 0,8 *
Время прохождения пути СВ по шоссе равно
С В _ уУ + 202-
0,2 ~ 0,2
Общая продолжительность переезда из А в В равна
а — х . Vr;e2-f-202
Эта сумма, которую обозначим через т, должна быть
наименьшей.
Уравнение
а — х , |Л*2 + 202 __
~^ ‘ о^ —т
представляем в виде
Умножив на 0,8, имеем:
-±-202 = 0,8т — а.
Обозначив 0,8т—а через k и освободив уравнение
от радикала, получаем квадратное уравнение
15х2—2kx + 6400—/г2=0,
откуда
—96000
Л~ 15
Так как k = 0,8m—а, то при наименьшем значении т
достигает наименьшей величины и k, и обратно ‘). Но
‘) Следует иметь в виду, что k>0, так как

151  Где устроить полустанок? 

чтобы х было действительным, 16&2 должно быть не
меньше 96 000. Значит, наименьшая величина для
16&2 есть 96 000. Поэтому т становится наименьшим,
когда
16/г2=96
откуда
и следовательно,
Х— ~Т5~~ 15 ~0’10-
Полустанок должен быть устроен приблизительно
в 5 км от точки D, какова бы ни была длина
a=AD.
Но, разумеется, наше решение имеет смысл только
для случаев, когда х<о, так как, составляя уравне-
ние, мы считали выражение о—х числом положи-
тельным.
Если х=а=s 5,16, то полустанка вообще строить не
надо; придется вести шоссе прямо на станцию. Так
же нужно поступать и в случаях, когда расстояние а
короче 5,16 км.
На этот раз мы оказываемся предусмотрительнее,
нежели уравнение. Если бы мы слепо доверились
уравнению, нам пришлось бы в рассматриваемом
случае построить полустанок за станцией, что было
бы явной нелепостью: в этом случае х>а и потому
время
а — х
0,8 *
в течение которого нужно ехать по железной дороге,
отрицательно. Случай поучительный, показывающий,
что при пользовании математическим орудием надо
с должной осмотрительностью относиться к получае-
мым результатам, помня, что они могут потерять ре-
альный смысл, если не выполнены предпосылки, на
которых основывалось применение нашего математи-
ческого орудия.

152  Где устроить полустанок? 

На главную страницу ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман. 
Школьная математика.  Математика в школе.

Околоadmin