Глава I. ПЯТОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ. Итоги повторного удвоения.
ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман ИЗДАНИЕ ДВЕНАДЦАТОЕ СТЕРЕОТИПНОЕ
Под редакцией и с дополнениями В. Г. Болтянского
Скачать 11-ое издание ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман в формате PDF в хорошем качестве, но без возможности каптирования на Главной странице ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Текст для быстрого ознакомления (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):
Итоги повторного удвоения
Разительный пример чрезвычайно быстрого возрастания
самой маленькой величины при повторном ее
удвоении дает общеизвестная легенда о награде изобретателю
шахматной игры1). Не останавливаясь на
этом классическом примере, приведу другие, не столь
широко известные.
ЗАДАЧА
Инфузория парамеция каждые 27 часов (в среднем)
делится пополам. Если бы все нарождающиеся
таким образом инфузории оставались в живых, то
сколько понадобилось бы времени, чтобы потомство
одной парамеции заняло объем, равный объему
Солнца?
Данные для расчета: 40-е поколение парамеций, не
погибающих после деления, занимает в объеме 1 куб. м\
объем Солнца примем равным 1027 куб. м.
РЕШЕНИЕ
Значит, сороковое поколение должно претерпеть
еще 90 делений, чтобы вырасти до объема Солнца*
1) См. мою книгу «Живая математика», гл. VII.
стр. 15 Итоги повторного удвоения.
Общее число поколений, считая от первого, равно
40 + 90 = 130. Легко сосчитать, что это произойдет на
147-е сутки.
Заметим, что фактически одним микробиологом
(Метальниковым) наблюдалось 8061 деление парамеции.
Предоставляю читателю самому рассчитать, какой
колоссальный объем заняло бы последнее поколение,
если бы ни одна инфузория из этого количества
не погибла…
Вопрос, рассмотренный в этой задаче, можно предложить,
так сказать, в обратном виде:
Вообразим, что наше Солнце разделилось пополам,
половина также разделилась пополам и т. д.
Сколько понадобится таких делений, чтобы получились
частицы величиной с инфузорию?
Хотя ответ уже известен читателям—130, он все
же поражает своею несоразмерной скромностью.
Мне предложили ту же задачу в такой форме:
Листок бумаги разрывают пополам, одну из полученных
половин снова делят пополам и т. д. Сколько
понадобится делений, чтобы получить частицы атомных
размеров?
Допустим, что бумажный лист весит 1 г, и примем
для веса атома величину порядка тг- Так как в последнем
выражении можно заменить 1024 приближенно
равным ему выражением 280, то ясно, что
делений пополам потребуется всего 80, а вовсе не
миллионы, как приходится иногда слышать в ответ
на вопрос этой задачи.
стр. 16 Итоги повторного удвоения.
На главную страницу ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Школьная математика. Математика в школе.

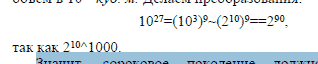


Comments