4. КОДОПОЗИТИВЫ.
Сборники Математики
|
Текст просто для быстрого ознакомления с темой в общих чертах (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):
| До сих пор не установилось определенного названия для — учебных материалов, используемых с помощью кодоскопа: их называют масками, диапозитивами, диапозитивами большого формата, кодопозитивами, листами для кодоскопа и т. п. Мы будем пользоваться термином «кодопозитивы». |
Рассмотрим педагогические возможности, появляющиеся
при применении кодопозитивов на уроках математики.
1. Преимуществом кодоскопа перед диапроектором является
то, что кодоскоп при той же мощности лампы дает значительно
более яркое изображение. Объясняется это тем, что кон-
денсорная линза кодоскопа имеет большую рабочую площадь,
57 КОДОПОЗИТИВЫ.
Так, если размер кадра стандартного диапозитива 24 X 36 (мм),
то кодопозитивы, выпускаемые отечественной промышленностью,
имеют размер кадра 100X140 (мм), т. е. рабочая площадь кодо-
позитива почти в 17 раз больше площади кадра диапозитива. Поэтому
(даже если учесть подсветку в виде отражающего зеркала,
применяемую в осветительной системе диапроекторов) кодоскоп
создает примерно в 10 раз. большую освещенность экрана, чем
диапроектор (при одинаковых размерах изображения на экране
и примерно одинаковой мощности источника света). Из сказанного
вытекает важное свойство: кодопозитивы можно использовать
в классе без затемнения (или при легких белых шторах в
яркий, солнечный день).
Например, серия кодопозитивов «Измерения на местности»1
предусматривает проецирование на экран или доску карты небольшого
района, видны несколько населенных пунктов, железная
дорога, сеть шоссейных дорог и. масштаб. Пользуясь масштабом,
учащиеся измеряют при помощи циркуля длины отдельных
участков шоссейных дорог. Благодаря кодоскопу эта работа
хорошо видна всему классу. После этого класс получает
самостоятельное задание (по вариантам) : найти расстояние по
шоссейной дороге между двумя данными (далеко расположенными)
пунктами, определить, какой из двух путей, ведущих из
одного пункта в другой, короче; бензиновые колонки расположены
в трех заданных пунктах — какая из, них ближе всего к
данному четвертому пункту и т. п. Эти задания учащиеся выполняют
в тетрадях, и потому для нормальной работы’ необходимо,
чтобы класс не был затемнен. В то же время учащиеся
должны видеть перед собой карту местности. Кодоскоп дает на
экране требуемую карту, хорошо видную всем учащимся в обыч-
ном- (незатемненном) классном помещении.
2. Как следствие большой освещенности экрана мы получаем
другую важную особенность кодопозитивов: изображение можно
проецировать прямо на доску, на которой можно мелом достраивать
изображение, дополнять его и т. д. Такую работу мы
рекомендуем проводить даже при использовании диапроектора 2,
однако, для того чтобы изображение на темном фоне доски было
достаточно ярким, диапроектор должен стоять близко к доске и
размеры изображения получаются, естественно, небольшие. Кодоскоп
же дает на темном фоне доски достаточно яркое изображение
больших размеров.
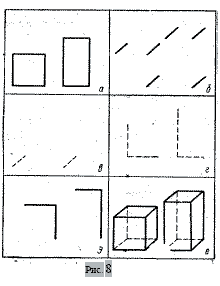
Приведем пример. В серии кодопозитивов «Изображение
прямоугольного параллелепипеда»3 имеются кодопозитивы, на
которых показаны отдельные элементы изображения прямоугольного
параллелепипеда (рис. 8). Проецируя второй из этих
1 Разработана Э. Ю. Крассом.
2 См. статью «Диафильмы и диапозитивы на уроках математики» в № 4-
журнала «Математика в школе» за 1971 г. *
3 Разработана Э. Ю. Крассом.
58 КОДОПОЗИТИВЫ.
кодопозитивов на доску, можно предложить учащимся достроить
имеющиеся линии до изображения прямоугольного параллелепипеда.
3. Отметим, что кодопозитивы накладываются учителем прямо
на конденсорную линзу кодоскопа. А так как кодопозитивы
ло математике представляют собой рисунки (как правило, штриховые)
или чертежи на тонкой прозрачной пленке, то появляется
возможность наложения нескольких кодопозитивов (до 4—5
штук) друг на друга для совмещения на экране нанесенных на
них изображений. Для более точного совмещения изображений
ла верхней части кодоскопа имеются установочные штифты, а
на кодопозитивах — пробивки.
Например, на первом кодопозитиве учитель может иметь
запись формулировки теоремы (что дано и что требуется доказать),
на втором — чертёж к теореме, на третьем — вспомогательные
линии, на четвертом — запись начала доказательства и
ла, пятом — заключительную часть доказательства теоремы.
Имея такой набор кодопозитивов, учитель может- сначала наложить
на конденсорную линзу первый из них и обсудить с
учащимися формулировку теоремы. Затем он может наложить
сверху второй кодонозитив, и на экране рядом с записью теоремы
появится чертеж. Теперь учитель имеет возможность обсудить
возможные пути доказательства теоремы. При этом, если
изображение проецируется на доску, можно попросить учащихся
наметить на доске мелом те вспомогательные линии, которые
потребуются для проведения
доказательства.
Если линии проведены *
неверно, их можно стереть,
а чертеж, создаваемый
на доске кодо-
скопом, останется. После
обсуждения можно
стереть все записи
на доске и наложить
третий кодопози-
тив с нанесенными на
лем вспомогательными
линиями. Когда чертеж
(дополненный вспомогательным
построени-.
ем) учащиеся перенесли
в свои тетради, учитель
накладывает четвертый
кодонозитив с
записью начала доказательства.
Наконец, ‘
лосде того нак эта
Рис. 8
59 КОДОПОЗИТИВЫ.
тетради,
учитель накладывает последний, пятый, кодопозитив и обсуждает
конец доказательства. Для того чтобы «стереть» все
написанное, достаточно снять кодопозитивы с кодоскопа, причем
при желании учитель может снова бегло повторить все доказательство,
накладывая кодопозитивы еще раз один за другим.
В этом большое преимущество преподавания с применением ко-
доскопа: при традиционной работе на доске учитель просто не
имеет времени, чтобы еще раз проглядеть все доказательство,
выполняя вспомогательные построения и проводя все записи.
В качестве другого примера обратимся снова к серии кодопозитивов
«Изображение прямоугольного параллелепипеда»
(см. рис. 8). Накладывая на линзу кодоскопа первый и третий из
этих кодопозитивов, мы получаем новую задачу на достраивание
изображения прямоугольного параллелепипеда; совмещение
третьего и пятого кодопозитивов дает еще одну задачу на достраивание
изображения прямоугольного параллелепипеда и
т. д. Наконец, совмещение все^х кодопозитивов, изображенных на
рис. 8, дает полное изображение прямоугольного параллелепипеда.
Ни диапозитивы, ни какое-либо иное средство обучения не.
дают возможности такого многократного наложения изображений.
Такую возможность (с множеством вытекающих отсюда методических
приемов преподавания) создают только кодопозитивы
Г. ‘
4. Описанная выше деятельность (объяснение доказательства
теоремы с применением кодоскопа) — лишь одна из многих
форм работы с листами для кодоскоп а.* Весьма существенно, что
при работе с кодоскопом (например, при объяснении новой теоремы,
как это было описано выше) учитель все время стоит лицом к
классу и может наблюдать за его работой (рис. 9). Это создает
ряд преимуществ по сравнению с традиционным методом работы
на доске. Учителю незачем смотреть на экран (или на доску),
так как на ярко освещенной конденсорной линзе он хорошо видит
нанесенное на кодопозитивах изображение и может маленькой
указочкой отмечать нужное место чертежа. Точно такое же
изображение будут видеть (в увеличенном виде) учащиеся на
экране (или на доске). А так как учитель стоит лицом к классу и
освобожден от необходимости делать записи на доске, то он
может наблюдать за классом и более эффективно руководить
его работой.
5. Следующая существенная черта кодопозитивов — возможность
смещения двух или большего их числа друг относительно
1 Впрочем, частичное наложение изображений (а именно совмещение изображений,
нанесенных на двух кадрах диафильма или двух диапозитивах) может
быть осуществлено при помощи магнитной приставки к диапроектору,
разработанной преподавателем математики средней школы № 706 Москвы
С. М. Кушулем,
60 КОДОПОЗИТИВЫ.
друга при их совместном показе. Это еще одна форма работы
с кодоскопом. Для иллюстрации рассмотрим следующий пример.
Учитель имеет два кодопозитива, на одном из которых изображена
координатная система с единичной (или более густой) сеткой
линий, а на другом — график функции у—х2, но без системы
координат. Причем первый из этих кодопозитивов имеет пробивку,
позволяющую неподвижно установить его на штифтах, а второй
пробивки не имеет и может при наложении на первый кодо-
позитив свободно смещаться по нему *. Имея два таких кодопозитива,
учитель может: а) по-разному накладывая второй кодо-
позитив, задавать вопросы о знаке коэффициентов р и q получающегося
трехчлена y—x2+px+q, о знаке дискриминанта, о характере
корней, о координатах вершины и т. д.г; б) иллюстрировать
сдвиги графиков, т. е. переход от графика y = f ( x ) к графику
y — f ( x + c ) + q на примере функции у=х2 (еще лучше для этого
иметь два кодопозитива с графиком у—х2— один черный и один
красный, чтобы можно было показать вместе и с х о д н ы й график
и с д в и н у т ы й ) ; в) задавать учащимся вопросы типа
«Как выглядит график трехчлена, у которого а<О, а корни оба
действительны и отрицательны?». И предлагать им отвечать на
эти вопросы, перемещая кодопозитив с параболой на кодо-
скопе; г) иллюстрировать решение квадратичных неравенств и
т. п. Более того, имея кроме кодопозитивов с изображениями ко-
1 Такие кодопозитивы имеются в серии «Квадратичная ‘функция», разработанной
В. Г. Болтянским и Г. Г. Левитасом.
2 Все такие положения параболы показаны на рис. 12 (стр. 77).
61 КОДОПОЗИТИВЫ.
ординатной сетки и параболы еще один, на котором нанесена
прямая линия, можно, по-разному накладывая кодопозитивы с
прямой и параболой на координатную сетку, иллюстрировать
графическое решение системы уравнений вида
, / y=x*+px+q,
\ ах+Ьу+с=0.
Возможность сдвига любого из кодопозитивов относительно
других важна не только для алгебры, но и для многих разделов
курса геометрйи (симметрия фигур, поворот, параллельный перенос,
равенство фигур и т. п.) . И в этом случае при показе изобра-
жений учитель стоит лицом к классу, а на конденсорной линзе
видит все, что происходит за его спиной на экране.
6. Учитель может не только пользоваться заранее подготовленными
изображениями, но и показывать при помощи кодоскопа
записи, непосредственно выполняемые на уроке. С этой целью
можно использовать любой лист прозрачного материала (цело-
фана, целлулоида и т. п.), который накладывается на конденсор-
ную линзу и на котором шариковой ручкой, фламастером, пастельным
карандашом или иным пишущим средством учитель
пишет формулы, изготовляет чертежи и т. п. На экране учащиеся
сразу же видят все записи, выполняемые учителем. Можно часть
записей заранее подготовить дома, а в классе лишь дополнять их.
Кодоскоп снабжен также специальной подвижной лентой/ так
что, исписав формулами рабочее поле, учитель имеет возможность —
передвинуть ленту и писать снова. При необходимости можно .
вернуть ленту назад и вспомнить ранее сделанные записи (что
выгодно отличает кодоскоп от классной доски). Если к этому
добавить, что надписи на ленте кодоскопа легко стираются, то
становится ясным, что кодоскоп вполне может заменить функции
классной доски. Футурологи-школоведы считают, что в недалеком
будущем (через 10—15 лет) классиая доска с мелом и
тряпкой, создающая в классе пыль и антисанитарию, начнет
сдавать свои позиции и уступать место оптической доске
(т. е. кодоскопу). Кстати дополнение чертежа учащимися (о чем
мы говорили выше при обсуждении доказательства теоремьг с
помощью кодоскопа) может производиться не мелом на доске, а
прямо на линзе кодоскопа (на листе целофана, наложенном
сверху на кодопозитив с доказательством теоремы). Это еще
раз показывает, что кодоскоп действительно может заменить
классную доску. »
7. Возникает естественный вопрос, нет ли таких функций
классной доски, которые не может заменить кодоскоп? Например,
как быть с опросом учащихся (ведь именно в связи с этим
учителя математики стремятся увеличить площадь классной
доски)? Легко понять, что именно в этом отношении листы для
кодоскоца создают особенно богатые возможности. В самом деле,
достаточно раздать опрашиваемым учащимся листы цело-
62 КОДОПОЗИТИВЫ.
фана и предложить им написать на них доказательство теоремы,
вывод формулы, решение задачи и т. п. Для опроса достаточна
вызвать учащегося «к кодоскопу» (вместо того чтобы вызывать
его «к доске») и предложить ему, наложив листок целофана на
конденсор кодоскопа, отвечать задание. Работа ученика будет
видна всем, ее можно, обсудить, а в случае ошибки вызвать к
кодоскопу второго ученика. При этом можно вести опрос одновременно
любого числа учащихся (посадив их, скажем, на первых
партах и предложив выполнять задание на листках целофана)
— лимитируют опрос здесь не размеры доски, которая просто
станет в будущем ненужной, а время учителя.
8. Существует несложный способ самодельного изготовления
кодопозитивов, применяемый учителем В. Н. Мораньковым.
Способ этот заключается в том, что используется фотопленка
(или рентгеновская пленка) размером 72X72 ( м м ) , которую нужно,,
вынув из пакета (прямо на свету), отфиксировать, т. е.
выдержать 10—15 минут,в растворе гипосульфита, а затем хорошо
промыть и высушить. На обработанной таким способом
пленке можно писать пером (или рейсфедером),, используя
обычные чернила или тушь. Имея элементарные навыки черчения,
учитель может изготовить на такой пленке превосходные
кодопозитивы. Более того, этим способом учитель может создавать
самодельные изображения, д о п о л н я ю щ и е серии кодопозитивов,
выпускаемых промышленностью. Изготавливать таким
способом самодельные д и а п о з и т и в ы затруднительно из-
за малого формата кадра.
9. Наконец, отметим еще один прием использования кодопозитивов
с целью создания удобных средств обучения.. Речь
идет о соединении нескольких кодопозитивов при помощи липкой
ленты, которую в городских условиях можно купить в магазинах
канцелярских товаров. В результате создается возможность,
поворачивая второй кодопозитив, накладывать его в нужный
момент на первый с точным совмещением изображений.
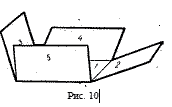
Можно также соединять липкой лентой и большее число кодопозитивов—
до пяти штук (рис. 10), причем, помещая основной
кодопозитив (помеченный цифрой 1 ) на конденсор кодоскопа,
можно в любой момент и в любой комбинации добавлять к нему
изображения других подклеенных с помощью ленты кодопозитивов.
Например, пять кодопозитивов а —д , изображенных на
рис. 8, можно склеить лентой по
схеме, показанной на рис. 10.
Несомненно, отмеченные выше
приемы работы с кодоскопом далеко
не исчерпывают всех педагогических
возможностей, создаваемых’
этим замечательным
прибором, и практика работы
учителей значительно обогатит в
Рис. 10
63 КОДОПОЗИТИВЫ.
будущем наши представления о дидактических функциях и методических
рекомендациях использования кодоскопа в условиях
средней школы.
64 КОДОПОЗИТИВЫ.



Comments