Точка и ее образ

Избранные в опросы теории преобразований подобия плоскости.
Точка и ее образ. § 6. Общие пары соответственных точек двух преобразований (часть 2).

З. А. Скопец, Л. И. Кузнецова

Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.

Избранные в опросы теории преобразований подобия плоскости.

З. А. Скопец, Л. И. Кузнецова

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Точка и ее образ. § 6. Общие пары соответственных точек двух преобразований. (часть 2).

1. Точка и ее образ при гомотетии лежат на одной прямой с
центром гомотетии.
З а д а ч а 1 . Доказать, что в любой трапеции точка пересечения
диагоналей, точка пересечения прямых, содержащих боковые
стороны, и середины оснований принадлежат одной прямой.
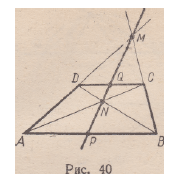
Р е ш е н и е . Пусть дана трапеция A BCD, точки Р и Q —
середины оснований АВ и CD соответственно, ( A D ) |») ( В С ) — М ,
I B D ] П [АС\ = N (рис. 40).

214 Точка и ее образ. 

Точка и ее образ

Так как отрезки АВ и CD параллельны и не конгруэнтны, то
существует гомотетия Нм, при которой точки Л и В отображаются
на D и С соответственно, а значит, [ А В \ отображается на \DC\.
Точка Р, середина отрезка АВ, отображается при гомотетии Ям
на середину отрезка DC, т. е. на точку Q. Но тогда М £ (P Q ) .
Аналогично существует гомотетия Н ы , отображающая точки
Л и В на С и D соответственно. При гомотетии H n точка Р также
отображается на Q. Следовательно, и точка N принадлежит прямой
PQ, что и требовалось доказать.
З а д а ч а 2 . Через вершины трапеции проведены прямые, параллельные
ее диагоналям. Доказать, что одна из диагоналей образовавшегося
параллелограмма параллельна основаниям трапеции, а
вторая диагональ проходит через точку пересечения диагоналей трапеции.
Р е ш е н и е . Дана трапеция ABCD, [ЛС] и [BD] — ее диагонали,
M N P Q — образовавшийся в результате построений параллелограмм
(рис. 41).
Так как отрезки А В и C D параллельны, то существует гомотетия
Н \ , отображающая [ А В ] на [ C D ] , К = \ А С ] f) [В£>], CD —
= а А В . При гомотетии Я к прямая M N , проходящая через точку
Л, отображается на прямую, проходящую через точку С и параллельную
прямой M N , т. е. на прямую PQ- Аналогично прямая N P
отображается при Я$*на Q M . Тогда Я“- ( N ) = Q , откуда следует,
что К € IjVQ].
Имеем:
Н% (Л) = С , Н% ( В ) = D, Н % (АО = Q ,
или
| QC |: | AN | = | QD |: | B N |.
Учитывая, что |ЛЯ| = \СР\ и |£W| = \ D M \ , находим:
| QC |: | СР | = | QD |: | D M |.
Последнее означает, что прямая М Р параллельна прямой C D .
2. Точка касания двух окружностей есть центр гомотетии, отображающей
одну окружность на другую.

215 Точка и ее образ.

З а д а ч а 3 . Доказать, что если через точку касания двух
окружностей провести произвольную прямую, то она пересекает
окружности вторично в таких точках, что радиусы, проведенные в
эти точки у параллельны.
Р е ш е н и е . Пусть М — точка касания окружностей со (О; г)
и сох ( 0 г ; /*), а — секущая, пересекающая окружности вторично
в точках А и А г (рис. 42). Требуется доказать, что [0ХЛг] || [ 0 А \ .
Рассмотрим гомотетию Н{0’мх). При этой гомотетии прямая а
отображается на себя, так как проходит через центр, а окружность
со — на сох. Тогда точка А, принадлежащая пересечению а и со,
отображается на точку, принадлежащую пересечению а и со!, но
отличную от М, значит, на точку Ах.
Так как [ О г А ^ \ — образ отрезка О А при гомотетии, то эти отрезки
параллельны.
З а д а ч а 4. Две окружности касаются внутренним образом
в точке А. Секущая а пересекает окружности в точках М, N, Р,
Q, расположенных последовательно. Доказать, что MAN = PAQ
(рис. 43).
Р е ш е н и е . Рассмотрим гомотетию НА, отображающую окружность
со на окружность Точки N и Р отобразятся при этой
гомотетии на точки N± и Pi, Nt £ со fl ( A N ) , Рх £ со П (ЛР).
Тогда прямая Л^Рх как образ прямой N P при гомотетии параллельна
ей. В силу параллельности прямых M Q и N x P i дуги M N X
и QPX конгруэнтны, а значит, конгруэнтны соответствующие нм
вписанные углы M A N X и QAPU т. е. MAN = ф4Р.

216 Точка и ее образ.

Околоadmin