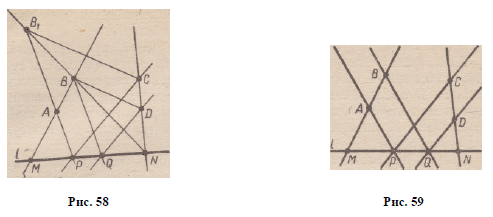Общие пары точек

Избранные в опросы теории преобразований подобия плоскости.
Общие пары точек. § 6. Общие пары соответственных точек двух преобразований (часть 6).

З. А. Скопец, Л. И. Кузнецова

Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.

Избранные в опросы теории преобразований подобия плоскости.

З. А. Скопец, Л. И. Кузнецова

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Общие пары точек. § 6. Общие пары соответственных точек двух преобразований. (часть 6).

10. Общие пары соответственных точек двух преобразований
подобия.
Понятие общих пар соответственных точек двух преобразований
(см. § 6) часто применяется в задачах на построение. Метод
общих пар по своей идее аналогичен методу множеств точек в решении
задач на построение.
* 3 а д а ч а 18. Даны прямая I и точки А, В, С, D вне ее,
причем ( А В ) П I = М , ( C D ) f] I — N и М Ф N . Построить на
прямой I точки Р и Q так, что ( А Р ) || ( B Q ) и ( С Р ) П ( D Q ) .
А н а л и з . Пусть точки Р и Q построены (рис. 58). Точка
Q есть образ точки Р при гомотетии Н м » В ) (имеющей центр в точке
М и отображающей точку Л на В). В то же время Q — образ
точки Р при гомотетии H(n’ D). Следовательно, (Р\ Q) — общая
пара точек гомотетий Нм; В) и ЯдГ °\ т. е. Н(м В) (Р) = Q и
Hn’ D ) ( P ) = Q . Но тогда Р — неподвижная точка композиции
я!у: с> о H t — в> (так как ( Н & = Н Т с>). ,
П о с т р о е н и е . 1. Строим образ точки’S при гомотетии
H t f ; С ) : С) (5) = В г (рис. 59).
, 2. Строим точку Р = 1 [ \ ( А В г ) .
3. Через точку В проводим прямую, параллельную прямой
А Р . Она пересекает I в точке Q .
Д о к а з а т е л ь с т в о и и с с л е д о в а н и е . Композиция
двух гомотетий с различными центрами есть либо гомотетия,
либо перенос, отличные от тождественного преобразования. В
первом случае существует единственная неподвижная точка —
центр. Она является точкой пересечения двойных прямых. П р я мая
I отображается на себя при каждой из гомотетий Hit’ В) и
Hn ‘ °\ следовательно, и при их композиции. По построению Вг =
= С)°Н(м В) ( А ) . Значит, (Л5^ также двойная п р я м а я рассматриваемой
композиции. Поскольку прямые I и А В г пересе-

224 Общие пары точек. 

Общие пары точек

каются, то композиция Н [ м : С ) о Н м ; В ) есть гомотетия, Р — ее
центр, т. е. Н/?; С) о Нм’ В) (Р) = Р. В этом случае задача имеет
единственное решение.
Если прямые I и АВг параллельны, т. е. композиция Ни*’* С)о
о Н{м’ В) — перенос, то задача не имеет решения.
З а м е ч а н и я . 1. Если М = N, то композиция Ни*’’ С)о Н{м; В)
может быть и тождественным преобразованием (В1 ~ А). В этом
случае задача имеет бесконечное множество решений.
2. Если только одна из прямых АВ и CD параллельна /,
то Р — неподвижная точка композиции гомотетии и переноса. Но
эта композиция есть гомотетия. Следовательно, задача имеет
единственное решение.
3. Если обе прямые параллельны /, то Р -г- неподвижная точка
композиции двух переносов, т. е. либо не существует, либо
таких точек, бесконечное множество.
Как видно, решение задач с применением понятия общей пары
соответственных точек двух преобразований основано на умении
выяснять, что представляет собой композиция двух частных видов
преобразований подобия, на умении строить неподвижную
точку конкретного преобразования подобия.
Изложенные выше элементы теории преобразования подобия
плоскости предназначены для учителя независимо от его опыта
работы в школе. Ряд вопросов названной теории практически не
освещен в известной или доступной учебной и методической литературе
на том уровне, на каком это требуется в современных условиях
учителю для повышения своего научно-методического
уровня, для получения ответа на интересующие его вопросы по
преобразованиям подобия плоскости.
Рассмотренные выше понятия аксиоматического характера,
детальные доказательства отдельных «очевидных» теорем, приведенные
нестандартные задачи с их подробным решением могут служить
лишь отправным пунктом для всесторонней методической
разработки всей темы в целом. Но такую разработку можно

225 Общие пары точек. 

начинать лишь тогда, когда определена теоретическая база изучаемого
вопроса, намечены важнейшие направления его изучения
с учетом запросов учителя и поставленных целей преподавания.
Как видно, теория преобразований подобия предполагает
глубокие знания теории перемещений, владение аксиоматическим
методом в пределах школьного курса геометрии, умение оперировать
не только с отдельными преобразованиями, но и с их композициями,
применять при решении задач признаки отдельных
видов подобий.
Можно рекомендовать учителю использовать материал статьи
для постановки факультативного курса по теории геометрических
преобразований, для проведения отдельных внеклассных занятий
по темам: 1) «Гомотетия, ее свойства и признаки», 2) «Неподвижная
точка преобразования подобия и ее построение», 3) «Преобразование
подобия второго рода и его применение при решении
задач», 4) «Композиции преобразований подобия в задачах» и др.
По каждому из названных выше направлений желательно
проводить дополнительные методические исследования, проверять
возможность использования введенных понятий в школьных условиях,
разрабатывать специальные циклы учебных задач в определенной
системе.
Полноценные методические исследования можно проводить,
на наш взгляд, на основе очерченной и достаточно полной (в
пределах действующих программ) математической теории. В этих
исследованиях, по-видимому, особое внимание следует уделить
разработке методики применения теории к решению задач.
Дополнительные сведения о преобразованиях подобия и их *
применении заинтересованный читатель найдет в учебно-методической
литературе, список которой приложен ниже.

ЛИТЕРАТУРА

1. А д а м а р Ж. Элементарная геометрия. М., Учпедгиз, 1957, ч. I.
2. Б о л т я н с к и й В, Г., Я г л о м И. М. Преобразования. Векторы.
М., Просвещение, 1964.
3. Г у с е в В. А., М а с л о в а Г. Г., С к о п е ц 3. А., Ч е р к а с
о в Р. С. Сборник задач и упражнений по геометрии для 6—8 классов. Пособие
для учителей. М., Педагогика, 1976.
4. К о к с т е р Г. С. Введение в геометрию. М., Наука, 1966.
5. К у з н е ц о в а JI. И., С к о п е ц 3. А. Метод подобия при решении
планиметрических задач. — Математика в школе, 1977, № 6.
6. М о д е н о в П . С . , П а р х о м е н к о А. С. Геометрические преобразования.
Изд-во МГУ, 1961.
7. П е р е п е л к и н Д . И. Курс элементарной геометрии. М. — Л.,
ГИТТЛ, 1948, ч. 1.
8. П о с т н и к о в М. М. Аналитическая геометрия. М., Наука, 1973.
9. С к о п е ц 3. А. Построение неподвижных точек аффинного преобра-
зования. — Математика в школе, 1972, № 3.
10. Я г л о м И. М. Геометрические преобразования. М., ГИТТЛ, 1955,
т. 1.
11. Я г л о м И. М., А т а н а с я н Л. С. Геометрические преобразования.
Энциклопедия элементарной математики, М., Физматгиз, 1963, кн. IV.

226 Общие пары точек.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика.  Математика в школе.

Околоadmin