Повороты

Повороты.

Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно: Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ ПЛОСКОСТИ И ЕЕ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. З. А. Скопец, Л. И. Кузнецова

(стр. 227-246)

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

§ 6. Повороты.  А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.

В школьном курсе геометрии определение поворота дается с
помощью понятия «величина угла». Покажем, что возможно другое
определение поворота, которое не предполагает наличия теоремы
о существовании величин углов.
О п р е д е л е н и е . Поворотом с центром О называется перемещение,
имеющее единственную неподвижную точку — точку О
или же являющееся тождественным преобразованием.
Заметим, что в отличие от других поворотов Е имеет не один
центр: любая точка плоскости — центр этого поворота.
Т е о р е м а 5.1. Если прямые а и b имеют общую точку О,
то композиция симметрий Sa и Sb — поворот с центром О.
Д о к а з а т е л ь с т в о . В случае совпадения прямых а и b
результат очевиден:
Пусть о и 6 — различные прямые. Очевидно, что О — неподвижная
точка Sa о Sb. Допустим, что X — неподвижная точка
Sa о Sbf отличная от О. Тогда
§ 5. Повороты
Sb(X) = Sa(X)=X1.

262 Повороты. 

Но существует единственная
осевая симметрия, переводящая
точку X в Хг. Действительно,
ось этой симметрии должна проходить
через середину отрезка
ХХх (§3) и быть перпендикулярной
(ХХх) (§ 4). Следовательно,
а = Ь. Это противоречит предположению.
Т е о р е м а 5.2. Если точки
А и В отличны от О, а расстояния | О А \ и | О В | равны, то сущест-
вует единственный поворот с центром О, переводящий А в В.
Д о к а з а т е л ь с т в о . Если точки А и В совпадают, доказательство
очевидно: искомый поворот — Е. Других таких поворотов
нет, так как единственный поворот, имеющий более одной <
неподвижной точки, — тождественное преобразование.
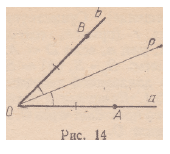
Пусть А ф В (рис. 14). Существует ровно два перемещения,
при которых А переходит в 5, а точка О неподвижна (A.IV.1).
Одно из них — симметрия Sp (р — прямая, содержащая биссектрису
угла АОВ). Но Sp ф Е и Sp имеет более одной неподвижной
точки. Отсюда сразу следует, что существует не^ более одного поворота
с центром О, переводящего А в В.

Существование такого поворота очевидно: по предыдущей теореме
Sp о Sa и Sbo Sp — повороты, причем
Sp o Sa (А) = Sp (А) = В, Sb о 5, (А) = Sb (В) = В.
Как мы только показали, поворот с центром О, переводящий
Л в В, представим в виде композиции двух симметрий, одна из которых
содержит сторону угла АОВу а другая — биссектрису этого
угла. Справедливо более общее утверждение.
Т е о р е м а 5.3. Всякий поворот представим в виде композиции
двух симметрий, оси которых пересекаются в центре поворота,
причем одна из осей может быть выбрана произвольно.
Д о к а з а т е л ь с т в о . Пусть р — произвольная прямая,
проходящая через центр О поворота /?, и поворот R переводит точку
А =£ О в некоторую точку В.
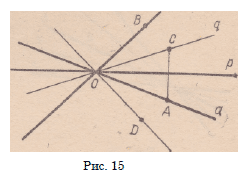
1) Обозначим через С точку Sp (А) (рис. 15). Существует единственная
прямая I (эта прямая
содержит биссектрису угла СОВ,
если С ф В, или это прямая ОВ,
если С = В), такая, что q проходит
через О и SQ (С) = SQ о
о Sp (Л) = В. Из теорем 5.1 и
5.2 вытекает, что SQ > Sp — R.
2) Осталось показать, что
существует такая симметрия Sn
что, домножив ее на Sp справа,
получим R.

263 Повороты. 

Обозначим через D точку Sp (В). Тогда \ОВ\= |ODj (Sp —
перемещение). Существует единственная проходящая через О
прямая г (прямая, содержащая биссектрису угла DO А, если
D=f= А, или а, если D = А, такая, что Sr (Л) = D).
Имеем: Sp ° Sr (А) = Sp (D) — В. Значит, Sp ° Sr — R.
Из доказанной теоремы следует:
■ У.5.1. Композиция поворота R с центром О и симметрии, ось I
которой проходит через О, является симметрией, ось которой также
содержит О.
Д о к а з а т е л ь с т в о . По теореме 5.3 существуют такие
прямые а и Ь, что R = St о Sa = Sb ° St.
Тогда
RoSt = (Sb о Sj) о S[ = Sb о (5г о 5;) = Sb,
S[° R = S[ ° (S[ о Sa) = (S[ о Sj) о Sa = Sb.
Т е о р е м а 5.4. Повороты с центром О образуют коммутативную
подгруппу группы перемещений плоскости.
Д о к а з а т е л ь с т в о . Обозначим через R множество поворотов
с центром О.
1) По определению Е € R.
2) R~l также является элементом R. Это свойство — очевидное
следствие определения поворота.
3) Композиция двух поворотов Rx и R2 с центром О — поворот
с тем же центром.
Действительно, по теореме 5.3 возможно такое представление
Ri и R2:
Ri — Sx° S.г, R2 = S2oS3
(оси симметрий Slt S2, S3 проходят через О). Тогда
Ях — R2 — (S, о S2) о (S2 о S3) = Sx о S| о 53 = 5, о 53.
Вследствие теоремы 5.1 S± ° 53 — поворот с центром О.
Остается доказать коммутативность.
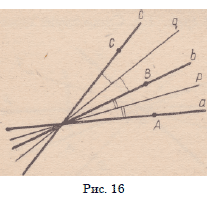
4) Для любых поворотов Rx и R2 с общим центром О
Ri ° R2 = R2 ° Ri-
Пусть Ri (Л) = В, R2 (В) = С; прямая р содержит биссектрису
угла АОВ, a q— биссектрису угла
СОВ (рис. 16).

Известно, что R1 = SboSp,
R2 = SqoS„
(см. доказательство теоремы 5.2).
Значит,
R2°Ri = (Sqо Sb) о (Sb о Sp) =
= Sq°SloSp = Sq°Sp. (1)
Рассмотрим теперь композицию
Рис. 16 Rx о R2:

264 Повороты. 

R.oR, =SboSp°S(,°Sb = [(SboSp)oS<l]oSb.
По теореме 5.1 Sb ° Sp — поворот с центром] О. Из У.5.1 следует,
что (Sb о Sp) ° Sq — осевая симметрия. Вследствие инволю-
тивности симметрии (S* ° Sp ° Sq)2 = Е, т. е.
Сравнивая (1) и (2), получаем: R± ° R2 = R2 ° Rt.
Поставим теперь такой вопрос: существуют ли инволютивные
повороты и сколько их? На вопрос «сколько?» можно ответить сразу:
в § 3 доказано, что всякое инволютивное перемещение F имеет
единственную неподвижную точку — середину отрезка XF (X),
где X — произвольная точка плоскости, отличная от О. Этими двумя
условиями: 1) О — единственная неподвижная точка F и 2) для
любой точки X плоскости точка О является серединой отрезка
XF (X) — отображение F плоскости на себя определяется однозначно.
Остается доказать, что F — поворот.
У.5.2. Если прямые а и b взаимно перпендикулярны, то поворот
$а° Sb — инволюция, причем Sa О Sb = Sb О Sa.
Д о к а з а т е л ь с т в о . Надо показать, что (Sa о Sj)-1 =»
= Sa о Sb. Но (Sa о Sj)-1 = Sb о Sa. Действительно,
Поэтому остается доказать, что Sa о Sb = Sb о Sa. Пусть О —
общая точка прямых а и Ь. Тогда
Рассмотрим такие точки А, В, С и D, лежащие на прямых а и Ь
(рис. 17), что | ОВ\ — | ОА |, | ОС\ =’ | OD|. Из перпендикулярности
прямых а и b сразу следует, что
Итак, образы трех неколлинеарных точек О, Л и С при перемещениях
Sa о Sb и Sb о Sa совпадают. Следовательно,
Sb
oSp°Sqo sb о SpoSQ = Е.
Умножив справа это равенство на Sg ° Sp, получим:
Sb ° Sp ° о Sb = SQ о Sp = Rx ° R%. (2)
(Sa ° Sb) о (Sb о Sa) — Sa о S2
b о Sa — 52 — E.
(Sa о Sb) (0) — Sb о Sa (0) = 0.
SaoSb (A) = SboSa(A)=B,
Sa ° Sb (C) = Sb a Sa (C) = D.
Будем называть точки Л и В симметричными
относительно точки О, если О —
середина отрезка АВ; точка О симметрична
самой себе.
b
G
а
О п р е д е л е н и е . Симметрией с В< О А
центром О называется отображение плоскости
на себя, при котором каждая точка
плоскости отображается на точку,
ей симметричную относительно О.

265 Повороты. 

Из У.5.2 и замечания, стоящего перед
этим утверждением, получаем:
У .5.3. Любая центральная симметрия
является перемещением.
Заметим, что можно, дать и такие определения:
1) центральной симметрией
называется инволютивный поворот, не являющийся
тождественным преобразованием,
2) симметрией с центром О называется
перемещение с единственной неподвижной
точкой О, при котором все прямые,
проходящие через О, переходят в себя.
Т е о р е м а 5.5 (основное свойство поворотов). Все выпуклые
углы, одна из сторон которых — луч с началом О, а другая — образ
этого луча при повороте R с центром О, попарно конгруэнтны.
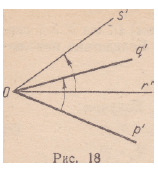
Д о к а з а т е л ь с т в о . Пусть р’ и г’ — лучи с началом О.
Образ р’ при повороте R обозначим через q’ (рис. 18), а образ г’ —
через s’, т. е.
q’-=R(p’), (1)
s’ = R(r’). (2)
^ Мы докажем теорему, если найдем перемещение, которое отображает
угол p’q’ на угол гУ. Достаточно показать, что существует
перемещение, при котором р’ переходит в г’, qr —в s’, а О остается
на месте. Таким перемещением является поворот R\ который
переводит р’ в г’:
г’ == R’ (рО (3)
(этот поворот вследствие теоремы 5.2 существует).
Воспользовавшись коммутативностью группы поворотов с общим
центром, а также соотношениями (1), (2) и (3), найдем образ луча
q’ при повороте R
R’ (<?’) = Я’ (R (р’)) — (R’ о R) (рО = (R о /?’) (рО = R (г’) = s’.
Теорема доказана.
§ 6. Измерение углов
Цель настоящего параграфа — доказательство недоказанной
в школьном курсе теоремы об измерении углов, т. е. теоремы о
существовании и единственности (при заданном условии нормировки)
меры, заданной на множестве углов плоскости и удовлетворяющей
известным условиям. Предварительно выделим некоторые нужные
в дальнейшем утверждения.
У.6.1. Если луч ОС содержится в выпуклом угле АОВ, то выпуклый
угол АОС — подмножество выпуклого угла АОВ.
(Доказательство см. на стр. 245.) Теорема 4.3 и это утверждение
позволяют ввести отношение порядка на множестве углов плоскости.
Из двух углов а и р , имеющих общую сторону ОА и содержа

266 Повороты. 

щихся в полуплоскости с границей О А, угол а больше угла (J,
если /La гэ l_.fi. Для выпуклых углов а и Р отношение порядка
устанавливается следующим образом. Выбирается некоторый луч
О А. В заданной полуплоскости с границей О А существуют углы
АОВ и АОС со стороной ОА, конгруэнтные /La и 2-fi соответственно.
Если Z-АОВ гэ Z.AOC, то по определению /La > Z.fi. На развернутые
и невыпуклые углы это отношение распространяется
естественным образом. Нетрудно убедиться, что так определенное
отношение антисимметрично и транзитивно, что любые два неконгруэнтных
угла сравнимы и что определение порядка не зависит
от выбора луча О А.
Угол АОС называется суммой углов.АОВ и ВОС, если пересечение
этих углов — их общая сторона, а объединение — угол АОС.
Очевидны предложения:
У.6.2. Если /La = /_ах + Z.a2, /Lfi = /Lfix + /Lfi2 и ^-ai ^
fi* Z-Px, Z_a2 = ZP2, to Z_a ZJfi.
У.6.3. лучи OxBt и 02B2 — биссектрисы, выпуклых углов
АхОхСх и Л202С2 соответственно, то выпуклые углы АхОхВх, А202Вг,
ВхОхСх и В202С2 попарно конгруэнтны.
Перейдем к основной части параграфа.
Угловой мерой называется функция р-, определенная на множестве
А углов плоскости и удовлетворяющая следующим требованиям:
1) ц (а) ^ 0 при любом а € А.
2) Меры, углов совпадают тогда и только тогда, когда эти углы
конгруэнтны.
3) Если определена сумма углов а и fi, то мера их суммы равна
сумме мер слагаемых.
Очевидно, что функция, сопоставляющая каждому углу число
нуль, есть тривиальная угловая мера. Встает вопрос: существует
ли хотя бы одна нетривиальная угловая мера и сколько их?
Т е о р е м а 6.1. Для любого неотрицательного числа С существует
не более одной угловой меры, сопоставляющей прямому
углу число С.
Д о к а з а т е л ь с т в о . Достаточно показать, что меры острых
углов е общей стороной, содержащиеся в некотором прямом угле е
той же стороной, определяются’ однозначно. Тогда из свойств меры
следует, что однозначно определяется мера любого угла.
В самом деле, вследствие теоремы 4.3 для любого острого угла а
существует конгруэнтный ему угол «0, уже получивший меру, и,
следовательно, по свойству 2 р (а) = у (а0). В силу условия аддитивности
(свойство 3) мера развернутого угла равна 2С, мера тупого
угла равна С + р (а) (а — острый угол); мера невыпуклого угла
равна 2С+р(ос)(а — выпуклый угол).
Из предположения о существовании меры сразу получаем:’
1°. Л е м м а ! Если /La < /Lfi, то р ( a ) р (|J).
Из У.6.3 следует:
2°. Л е м м а 2 . Если Ъх и Ь2 — биссектрисы выпуклых углов

267 Повороты. 

и агс2 и /La^ ^ Z_a2c2, то
(/LaА) = ц (Z. сА) = I* с262) = -^n(Z. axq) = i ц (Z. a2c2).
Ядея доказательства.
Пусть существует угловая мера р,, причем мера прямого угла
равна С. Проведя биссектрису прямого угла, получим два конгруэнтных
угла, причем мера каждого из них равна Разделив каждый
из них пополам, мы снова определим меру каждого из получающихся
углов и т. д. Для удобства будем называть построенные лучи
6-лучами, а углы, ими образованные, — 6-углами, точки пересечения
8-лучей с отрезком CD — 8-точками. С помощью построения
6-лучей можно определить меры счетного множества острых углов.
Естественно попытаться доказать, что доопределить эту меру до
множества всех острых углов можно единственным образом. Для
этого воспользуемся следующей конструкцией.
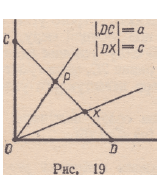
На сторонах прямого угла возьмем точки D и С, удаленные от
вершины О на расстояние 1 (рис. 19). Пусть | DC\ = а. Любой угловой
мере можно сопоставить функцию /ц с областью определения
10, а]: каждому числу х (0 ^ х ^ а) соответствует некоторая точка X
отрезка CD (|XD| = х): лучу ОХ соответствует число fi (Z.DOX).
Положим flx (х) = [i (Z.DOX).
Множество значений /ц совпадает с множеством мер всех острых
углов. В самом деле, пусть [х0 — мера острого угла DOP. Луч ОР
пересекает отрезок DC в некоторой точке Р. Тогда /ц (\DP\) = ц0.
Функция fn монотонна: если х > у, \DX\ = x, \DY\ = y ‘,
то в силу предложения У.6.1 ZJDOX > Z.DOY. По лемме 1
М*) >Цу)-
Если [хх и |х2 — различные меры, то р,2 (Z-DOX) ф (Z-DOX)
для некоторого острого угла DOX. Тогда и /n(|ZM |)=^=/u2(|Z.Z)OX|).
Значит, доказав, что функция /)Х определяется однозначно, мы докажем
теорему единственности угловой меры при заданном условии
нормировки, а доказав, что /ц существует, и проверив свойства угловой
меры, докажем теорему существования. При этом будем опираться
на следующий известный результат из анализа:
3°. Л е м м а 3. Если монотонная функция
ф определена на всюду плотном в [а, Ь]
множестве X, содержащем а и Ь, и ф (X)
всюду плотное на [а, р] множество (ф (а)=
= а, ф (b) = Р), то существует одно и
только одно монотонное продолжение ф*
функции ф на отрезок [а, Ь]. Это продолжение
непрерывно.
(«Всюду плотность» X означает, что любой
отрезок с концами из [a; b] содержит точки
множества X).

268 Повороты. 

единственности
достаточно показать: множество 5 всех 5-точек
всюду плотно на отрезке CD, а множество мер углов, определяемых
fi-точками, всюду плотно на отрезке [О, С].
4°. Л е м м а 4. Для любого натурального п существует такое
состоящее из 2п + 1 точки подмножество Вп отрезка CD, что:
с) В0 = D, В2п = С; б) | DBi+1 | > | DBt |; е) Z.BL ОВш &
& A.BjOBj+1 при любых натуральных i, j, меньших 2п .
Это утверждение верно при п = 1. В самом деле, проведем биссектрису
ОВ угла COD. Тогда выпуклые углы BOD и ВОС конгруэнтными
{С, В, D) — искомое множество. Последующие этапы доказательства
по индукции — следствия предложения У .6.2, леммы 1 и 2.
оо
5°. Лем м а 5. Пусть В — (J Вп . Множество значений фупк-
П~ 1
ции /ц, определенной на множестве { х \ х — |50Х|, X С 5}, всюду
плотно на [О, С]. Значения /ц на этом множестве определяются
однозначно.
Пусть Вп — произвольное множество, удовлетворяющее условиям,
сформулированным в лемме 4. Из свойств Вп получаем:
k—1
2 ^-Bt OBi+1 ^ Z.B0OBk при любом натуральном k, меньшем 2я.
i=о
/_BjOBJ+1 s* /LBiOBi+1 при любых натуральных i, /, меньших 2″.
Так как У! Z.5; OBi+1=Z.B0OB2n, а (х (Z.В1ОВ2П)—С, послелога
вательно применяя У.6.3, свойства меры и лемму 2, получаем, что
при любом натуральном i, меньшем 2я,
»(/LBt OBi+1) = £, ti (Z b0obl ) = £ i.
oo
Остается заметить, что множество Р = [) Рп, где Рп =
п=1
— {
6°. Л е м м а 6. Множество В всюду плотно на отрезке [0, а].
Рассмотрим несколько случаев: а) М € В, N £ В.
Пусть точки М и N принадлежат некоторому множеству Вп,
М = Bt, N = Bj. Если разность i и / четна, то точка пересечения
биссектрисы угла 5(- О В} есть точка В. Если эта разность нечетна,
то эта точка принадлежит В„+1, а значит, и В.
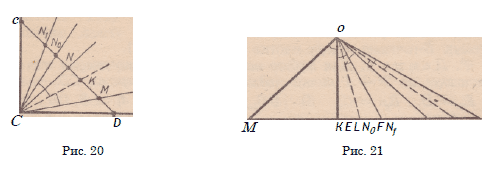
б) М € В, N £ В. Для определенности положим |DiV| > \DM\.
Допустим, что отрезок M.N не содержит fi-точек, кроме М.
Тогда все 5-точки отрезка СМ (кроме М) принадлежат отрезку CN.
Рассмотрим множество Ф = {|СХ| : X € 5 П [CW]}. Очевидно,
что Ф счетно. Пусть /0 — точная верхняя грань этого множества;
N0 — такая точка, что |CW0| = /0 (рис. 20).

269 Повороты. 

Проведем биссектрису ОК угла MON0. Так как | CN0\ = sup Ф,
то существует 5-точка Nt отрезка CN0, такая, что /.N0ONX <
< NO К. N х и М — 5-точки. Значит, биссектриса угла N^OM —
5-луч. Если мы докажем, что эта биссектриса пересекает отрезок
MN0, то докажем лемму 6: согласно сделанным предложениям внутренние
точки отрезка MN0 не принадлежат 5.
Приходим к следующей задаче (рис. 21):
Д а н о : A.N0OK ~ /.МОК, Z.N0ONx < /.KON0.
Д о к а з а т ь : биссектриса угла MON± пересекает’ отрезок
MN о.
Д о к а з а т е л ь с т в о . Пусть Z-KOL ^ /.NqON^ Тогда
L £ l/OV0], (По условию Z-NqONx </_KON0). Проведем биссектрисы
выпуклых углов KOL (луч ОЕ) и N0ONX (луч OF). Вследствие
конгруэнтности углов KOL и N0ONlt применяя У .6.2, получим:
Но /-EOF ^ /.EOF. /.KOE^AFON. Поэтому
/. KOF **/. EONv (2)
Из 1 и 2 следует: /-МОЕ s* /LEONx. Биссектриса угла, отличного
от развернутого, единственна. Значит, [05) — биссектриса
угла MONx. При этом 5 € [MN01.
Последний случай (М 6 5, N € 5) рассматривается аналогично.
Тем самым лемма 6, а’следовательно, и теорема единственности
доказаны.
Т е о р е м а 6.2 (существования). Для любого положительного
С существует угловая мера, сопоставляющая прямому углу число С.
Д о к а з а т е л ь с т в о . Существование функции /ц доказано.
Положим меру острого угла DOX равной /й (|DX|). Для любого
острого угла плоскости а существует угол |3 со стороной OD, конгруэнтный
а и содержащийся в /.COD. Положим р- (а) = ц (ji).
Тем самым определены меры всех острых углов. Проверим, что на
множестве острых углов, суммы любых двух из которых — острые
углы, для построенной меры выполнены все свойства угловой
меры.
Z КОЕ EOL ^Z N0OF ^Z FONv

270 Повороты. 

Первое свойство, очевидно, выполняется: по определению
Проверим справедливость второго свойства.
Если Z.a ^ Z.P, то по определению меры острого угла р (а) =
= р (Р). Докажем обратное. Пусть р (а) = р (Р). Отложим углы а
и р, содержащиеся в Z.COD, от луча OD. Стороны этих углов пересекают
отрезок CD в некоторых точках X’ и X» (по предположению
L.a и Z-P — острые углы). Если X! — X», утверждение доказано.
Пусть \DX»\ > \DX’\ (рис. 22).
Множество 5-точек всюду плотно на [OD\. Пусть В’, В» — произвольные
5-точки отрезка XX’ (\DB’\ < \DB»\). В ходе доказательства
теоремы единственности показано, что — строго монотонная
функция (это следствие строгой монотонности функции /ц
на множестве В). Поэтому
р (Z-DOX’) < р (Z. DOB’) < р (Z. DOB») < р (Z. DOX»).
Полученное неравенство противоречит условию. Значит, Х! —
= X» и Z^a = Zip.
Остается проверить аддитивность построенной меры. Так как
всякий острый угол а + Р можно отложить от луча OD, достаточно
проверить это свойство для углов, у каждого из которых одна из
сторон — луч OD.
Первый случай’, стороны углов — 5-лучи (рис. 23).
Пусть В’, В» — 5-точки; \ОВ»\ > \ ОВ’\. Покажем, что
р (ZDOB0 + р (Z. В’ОВ») = р (Z. DOB»).
При некоторых п, /, / точки В’, 5″ принадлежат Вп и имеют
номера t, / соответственно (г > /). Из свойств }ц и определения р
следует:
р(ос)>0.
Z. 5г 05,- в Z. DOBi_j, U (| DB» |) = | /,
М|05’|) = |<, (|D5w|) = £ ( i — / ) .
По определению угловой меры
р (Z. BfiBj) = £ ( / — / ) , р (Z. Z)05′) р (Z. D05″) = | /.

271 Повороты. 

В итоге получаем:
fi (ZDOB’) +р(/.В’ОВ») = | j + — /) =
= £(- = p(ZD05″).
Второй случай1, хотя бы одна из сторон
углов а и Р не является fi-лучом.
Рис. 24 Пусть /.POD = ZQOP + ZQOD
(рис. 24). Так как В всюду плотно,
можно выбрать последовательность В-точек {Р«}, {Рп},
{Qn}> {Q«}, таких, что lim \DP’n\ = lim \DP»n\ = \DP\-, lim | D&|=
rt-voo П-+СО П-+СО
= lim |DQ„| = |DQ|, причем последовательности {IDP^},
«-►00
{|DQ„|} возрастают, а последовательности {\DP»n\}, {| DQJ} убывают.
/р, — непрерывная функция. Поэтому
U (I PD\) =fi (ZPOD) = lim I dp;| = lim I DP; |,
n-*oo П-+00
ft (| QD I) = (i (Z QOD) = lim | DQ’n 1 = lim | DQ’\.
П-+ЭО tl-+ OO
При любом n /_P»nOQ’n > /.POQ > /.PnOQn. Углы P»nOQ’n и
PnOQn являются 5-углами. Для 5-углов аддитивность р доказана.
Поэтому
(| dp; |) (| dq; |) >р <z poq) > (| dp; d — /„ (| dq; t).
Переходя к пределу, получаем:
ц (Z POD) — p (Z QOD) > fi (Z POQ) > p (Z POD) — p (ZQOD).
Итак,
p (Z POQ) = p (Z POD) — p (Z QOD),
p (Z POD) = p (Z POQ) + p (Z QOD).
Тем самым мера на множестве острых углов построена. В начале
доказательства теоремы единственности показано как эта
мера продолжается на все множество углов. Можно сформулировать:
Т е о р е м а 6.3 (основная теорема). Для любого неотрицательного
числа С угловая мера, сопоставляющая прямому углу
число С, существует, и притом только одна.
Проведенное доказательство основной теоремы не опирается
на аксиому параллельных, т. е. это утверждение относится как
к евклидовой планиметрии, так и к планиметрии Лобачевского. В
работах С. Гиндикина [4] и А. Донеддю [7] содержатся другие доказательства
этой теоремы, существенно опирающиеся на аксиому
параллельных.

272 Повороты. 

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика.  Математика в школе.

Повороты