Некоторые следствия из аксиомы порядка на плоскости.
Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):
Скачать бесплатно: Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ ПЛОСКОСТИ И ЕЕ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. З. А. Скопец, Л. И. Кузнецова
(стр. 227-246)
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
§ 3. Некоторые следствия из аксиомы порядка на плоскости. А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.
Будем говорить, что точки А а В разделены прямой р, если отрезок
А В пересекает прямую р.
А . I I 1.4. Любая прямая р плоскости разбивает множество не
принадлежащих ей точек плоскости на два непустых подмножества,
таких, что:
а) любые две точки, принадлежащие разным множествам, разделены
прямой р;
б) любые две точки, принадлежащие одному и тому же множеству,
прямой р, не разделены.
Аналогично доказательству единственности разбиения прямой
принадлежащей ей точкой доказывается единственность разбиения
(указанного в аксиоме А.II 1.4) плоскости любой прямой, фигура,
состоящая из таких точек плоскости, любые две из которых не
разделены прямой р, называется открытой полуплоскостью с
границей р. Объединение открытой полуплоскости и ее границы
называется полуплоскостью. Открытые полуплоскости с границей
р обозначаются далее а’р и ар; полуплоскости с этой же границей
обозначаются а’р и ар (часто, если при этом не возникает недоразумений,
индекс р будет опускаться).
Из аксиомы A.III.4, в частности, следует: ар U ар *=* а\р,
&р Г) ~ 0» 7^ 0» ®р 0 •
У.3.1. Плоскость содержит бесконечно много прямых.
Д о к а з а т е л ь с т в о . Одна прямая существует (А.1.2).
Обозначим ее через р. Существует точка X, не принадлежащая р
(по A . I I I . 4 а\р^= 0). Если А и В —- различные точки прямой р,
то прямые АХ и ВХ различны. Действительно, допуская, что
237 Некоторые следствия из аксиомы порядка на плоскости.
(Л л) = (Вл) — <7, по теореме 2 Л получаем (так как Л t р П <7
и В £ р П <7)» что р = q. Но тогда X 6 р, что противоречит допущению.
Остается заметить, что на прямой р бесконечно много точек
(А Л11.3).
Напомним, что фигура Ф называется выпуклой, если вместе с
любыми двумя ее точками Л и В она содержит и соединяющий их
отрезок (пустое множество и точка по определению также считаются
выпуклыми фигурами). Очевидным следствием этого определения
является утверждение: пересечение двух выпуклых фигур — выпуклая
фигура.
Т е о р е м а 3.1. Полуплоскости и открытые полуплоскости —
выпуклые фигуры.
Д о к а з а т е л ь с т в о . Пусть Л и В — произвольные точки
открытой полуплоскости а’р. По определению открытой полуплоскости
отрезок Л В не содержит точек прямой р. Остается доказать,
что этому отрезку не принадлежат и точки ар. Допустим противное:
существует такая точка С отрезка АВ, что С £ а’р. Тогда Л и С
разделены прямой р, и поэтому существует точка D прямой р,
принадлежащая отрезку АС.
Заметим теперь, что [АС] с [АВ] (У.2.6). Значит, D 6 [АВ].
Но точки Л и В не разделены прямой р. Получено противоречие
с допущением Л 6 ар> В £ ар . Выпуклость ар доказана.
Полуплоскость а’р — объединение открытой полуплоскости ар
и прямой р. Вследствие доказанной выпуклости а’р и очевидной
выпуклости прямой остается показать, что если Л 6 а Р и В £ р,
то [ЛВ] cz а’р. Это также легко доказывается от противного.
У.3.2. Если начало О открытого луча qo принадлежит прямой
р, то q’o либо совпадает с ро или ро, либо содержится в одной из
открытых полуплоскостей с границей р.
Д о к а з а т е л ь с т в о . Если существует точка Л открытого
луча qo, принадлежащая р, то р = q и вследствие доказанной единственности
разбиения прямой q’o ■= ро или q’o — Ро- Пусть q0
точек прямой р не содержит. Возьмем произвольную точку В,
принадлежащую q’0. Тогда либо В £ а ‘ , либо В £ а” (A.III.4).
Пусть для определенности В 6 а
р- Допустим, что существует
такая точка С 6 q’0, что С 6 а’р- Тогда точки В и С разделены прямой
р, и, значит, лучу q’0 принадлежит точка прямой р. Пришли
к противоречию со сделанным ранее допущением q’0 [\ р — 0.
У.3.3. Круги (окружности) плоскости содержат бесконечно много
точек.
Д о к а з а т е л ь с т в о . Через любую точку О плоскости
проходит бесконечно много прямых (почему?). На каждой из этих
прямых имеются две точки X и Y окружности радиуса г с центром
О (A.111.3). Любая точка отрезка XY (вследствие A . I I I . 3 их также
бесконечно много) принадлежит кругу с центром О.
238 Некоторые следствия из аксиомы порядка на плоскости.
У.3.4. Каждый круг (окружность) плоскости имеет единственный
центр и радиус.
Д о к а з а т е л ь с т в о . Пусть
{ Х : | 0 1Х|<г1} = {Х:|02Х|<г2}.
Надо доказать: Ох = 02, гх = г2.
Допустим, что гх > г2. На произвольной прямой, проходящей
через О, возьмем различные точки А а В, такие, что | ОхА \ — \ Ox B\—
— rv Точки А и В принадлежат множеству {X: | ОхХ I ^ Гх). Из
условия следует также, что А и В — точки фигуры {X : 102Х | <>2},
поэтому |02Л | < ; г2, | 0 2В | ^ г2. Вследствие A.11.3 | Л 0 2 | + | 0 2Б | ^
АВ| = 2rl t откуда 2г2 ^ 2rv Последнее неравенство противоречит
допущению гг > г2. Следовательно, гх — гг — г.
Докажем теперь, что Ох = 02. Точка 02 не может находиться
вне прямой АВ, так как в этом случае по неравенству треугольника
имеем: | Л 0 2 | + \Ог В\>\АВ\, т. е. 2г <2г. Но на прямой АВ
имеется лишь одна точка, удаленная и от Л, и от В на расстояние
г. Это точка Ov Значит, Ох = 02.
При доказательстве существенное значение имели порядковые
свойства плоскости. Это не случайно: в дискретном пространстве
(см. пример, § 1), как легко проверить, для любых двух точек Ох
и 02 круги с центрами Ох и 02, имеющие радиусы 1 и 2, совпадают
со всем пространством. Следовательно, в дискретном пространстве,
в котором аксиомы порядка не выполняются, предложение
У.3.4 не справедливо.
У.3.5. 1) Фигуры {X 😐 О Х | < г } и { X : | ОХ| > г} — открытые
подмножества плоскости. 2 ) Граница круга (О, г) — окружность
(О, г ) .
Д о к а з а т е л ь с т в о . 1) Пусть Ох — такая точка, что
| ООх \< г. Докажем, что круг с центром Ог радиуса г — | ООг | есть
подмножество круга (О, г).
Возьмем произвольную точку X круга с центром Ох радиуса
г—| ООх|. Тогда
Ю Х | < | 0 10 | + | 0 1Х | < | 0 0 1| + Г — | 0 0 1| = Г .
Значит, X 6 Кр (О, г) и Кр (Ог , г — | OOJ) с= Кр (О, г).
Аналогично доказывается, что (X : |0Х| > г} — открытое подмножество
плоскости.
2) Пусть Л 6 Окр (О, г). Рассмотрим круг произвольного радиуса
гх с центром Л. Точки луча АО, удаленные от Л на расстояние,
не превышающее гх и г, принадлежат кругу (О, г), и кругу (Л, гх ).
Далее рассуждения очевидны.
К числу немногих понятий школьного курса, вводимых без
точных определений, относится понятие «ломаная» (простая). Дадим
определение этого понятия здесь.
Ломаной называется фигура, которую можно представить в виде
объединения п отрезков ЛхЛ2, Л2Л3, …, Ап Ап +Х (п — произ
239 Некоторые следствия из аксиомы порядка на плоскости.
вольное натуральное число, не меньше 2), таких, что: а) любой из
концов этих отрезков принадлежит не более двум отрезкам; б) пересечение
отрезков, не имеющих общего конца, пусто; в) отрезки, имеющие
общий конец, не лежат на одной прямой.
Если точки Ах и Лл+1 различны, то ломаная — объединение
отрезков АХ А2 , А2 А3 , …, А„А„+1 — называется незамкнутой
(обозначается ЛХЛ2 . . . Ля+1). Если точки Ai и Ап+1 совпадают,
то эта ломаная называется замкнутой (обозначается Аг А2 … Ап ).
Точки Лх, Л2, …, Аи называются вершинами ломаной А ХЛ 2 … Л*’,
а отрезки Аг А2 , Л2Л3, Ak _x Ak —звеньями этой ломаной.
Длиной ломаной называется сумма длин ее звеньев.
Т е о р е м а 3.3. Ломаная, соединяющая точки А и В, которые
лежат в различных открытых полуплоскостях с границей р, пересекает
прямую р по меньшей мере в одной точке.
Д о к а з а т е л ь с т в о . Докажем эту теорему по индукции.
Рассмотрим двузвенную ломаную АСВ. Если отрезок АС не имеет
общих точек с р, то точка С лежит в той же открытой полуплоскости
с границей р, что и точка А. Следовательно, точки В и С разделены
прямой р, т. е. отрезок ВС имеет общую точку с р.
Допустив, что теорема доказана для (п — 1)-звенной ломаной,
докажем ее для произвольной и-звенной ломаной АССгС2… С п_2В.
Если точка Сп_2 лежит в той же открытой полуплоскости, что
и Л, то точки С„_2 и В лежат по разные стороны от р, тогда отрезок
ВСп_2, а значит, и ломаная АССгС2 … Сп_2В имеют общие
точки с р. Если же С„_2 лежит с Л по разные стороны, то по предположению
индукции ломаная АССг … Сп_2 имеет общие точки с р.
Пусть А, В и С — точки, не принадлежащие одной прямой.
Треугольником ABC называется пересечение полуплоскостей с
границами АВ, ВС и АС, содержащими точки С, А и В соответственно.
Отрезки АВ, ВС и АС называются сторонами этого треугольника,
а точки А, В и С — его вершинами.
Т е о р е м а 3.4 (Паша). Если прямая пересекает сторону треугольника,
то она имеет общую точку и с одной из двух других его
сторон.
Д о к а з а т е л ь с т в о . Пусть прямая р пересекает сторону
АВ треугольника ABC. Тогда точки А и В разделены прямой р и,
значит, лежат в различных открытых полуплоскостях с границей р.
Если точка С лежит в той же открытой полуплоскости с границей
р, что и Л, то прямая р пересекает сторону ВС; если же точки
Л и С лежат по разные стороны от р, то р пересекает сторону АС.
Наконец, если С 6 р, то р имеет общие точки и с [ВС], и с [АС].
Назовем множество Ф точек связным, если для любых двух
точек этого множества существует ломаная или отрезок, целиком
содержащиеся в Ф. Если множество точек, не принадлежащих
фигуре Ф, представимо в виде объединения п непересекающихся
связных множеств и не представимо в виде меньшего числа связных
множеств, то будем говорить, что Ф разбивает плоскость на п
связных подмножеств. В этих терминах, пользуясь аксиомой
240 Некоторые следствия из аксиомы порядка на плоскости.
А.Ш.4 и теоремой 3.3, можно сказать: любая прямая разбивает
плоскость на два связных подмножества.
Доказанная теорема Паша в системе Гильберта принята в качестве
аксиомы. Нетрудно проверить, что все гильбертовы аксиомы
принадлежности и порядка на данный момент доказаны. Поэтому
вполне законна ссылка на «Основания геометрии», где выводится
(стр. 409—419) «теорема Жордана для многоугольных областей»:
Т е о р е м а 3.5. П ростая замкнутая ломаная Р разбивает плоскость
на два связных подмножества, одно из которых содержит хотя
бы одну прямую, а другое не содержит ни одной прямой.
Открытое связное множество называется областью.
У.3.6. Любая открытая полуплоскость является выпуклой областью.
Д о к а з а т е л ь с т в о . Связность открытой полуплоскости
является очевидным следствием ее выпуклости. Следовательно,
остается доказать, что открытая полуплоскость ар есть открытое
множество, т. е. для любой точки А £ ар существует круг с центром
А, содержащийся в ар. Для доказательства воспользуемся свойствами
непрерывных функций.
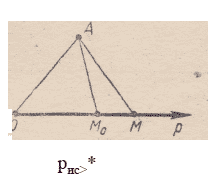
Введем на прямой р координаты (рис. 1). Каждому действительному
числу t соответствует некоторая точка М (/) прямой р (.x^=t).
Рассмотрим функцию / (/) = \АМ (/)|.
1) № -> QO При t00.
Действительно, в силу неравенства треугольника,
f(t) = \AM\>\\OM\—\OA\\ = \\t\ — \OA\\.
Расстояние | ОА | постоянно. Следовательно, для любого N > О,
при U| > N + \0А\, получим:
f (0 > 11*1 -\0А II >\N + \0А | — | О Л | | = Л Г .
2) Функция f (t) непрерывна в каждой точке t € R. В самом
деле, возьмем любое е> 0 и положим 6 = е. Тогда для любого
t, такого, что \t— 41 < б, имеем:
1/(0- / ( д | = \\АМ I -1АМ0 I I < IММ01 = |■/ -101 < 8.
Как это известно из анализа, непрерывная на всей прямой и
стремящаяся к бесконечности при | / | — > оо функция достигает минимума
в некоторой точке t*. Таким образом, существует точка
М (/*) прямой /?, такая, что М* —наименее удаленная от А точка
прямой р.
Отметим, что \АМ* \¥=0, так как в
противном случае А £ р. Обозначив через
г расстояние |АМ*|, сразу получаем, что
к р у г ^4, y j содержится в открытой полуплоскости
а . Очевидно также, что каждая
точка прямой р — граничная точка открытой
полуплоскости а’р.
241 Некоторые следствия из аксиомы порядка на плоскости.
Итак, множество точек, не принадлежащих прямой р, представимо
в виде объединения двух выпуклых областей — ими являются
открытые полуплоскости а’р и а». Объединение этих областей не
является областью (теорема 3.3). Следовательно, справедлива теорема
3.5.
Т е о р е м а 3.5. Любая прямая разбивает плоскость на две
выпуклые области.
Из этой теоремы следует также, что связные множества, на которые
по теореме 3.4 любая простая замкнутая ломаная разбивает
множество не принадлежащих ей точек, являются областями.
242 Некоторые следствия из аксиомы порядка на плоскости.
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика. Математика в школе.