Свойства осевой симметрии

Свойства осевой симметрии.

Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно: Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ ПЛОСКОСТИ И ЕЕ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. З. А. Скопец, Л. И. Кузнецова

(стр. 227-246)

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

§ 3. Свойства осевой симметрии.  А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.

Т е о р е м а 3.1. Множество точек, равноудаленных от двух
данных, есть прямая.
Д о к а з а т е л ь с т в о . Как показано в § 2, для любых точек
А и В плоскости существует прямая р, относительно которой
эти точки симметричны. Каждая точка О этой прямой равноудалена
от А и В, так как симметрия сохраняет расстояния и S„ (Л) = В,
Sp (О) = О.
Вне прямой р точек, равноудаленных от Л и В, не существует.
Действительно, на прямой АВ таких точек (кроме середины М
отрезка АВ) нет. Если же X $ (АВ) и X i р, то одна из точек Л и
В лежит в той же открытой полуплоскости с границей р, что и точка
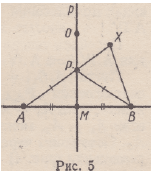
X. Пусть для определенности это точка В (рис. 5). Тогда отрезок
АХ пересекает прямую р в некоторой точке Р.
Точки Р, X, В не лежат на одной прямой. По неравенству треугольника
|РХ| + |РВ|>|ХВ|.
Так как по доказанному |ЛР|=|РВ|,
отсюда имеем:
|РХ| + |РЛ|>|ХВ|.
Точка Р лежит между Л и X. Значит,
последнее неравенство можно переписать
так:
\АХ\>\ВХ\.
Прямую, состоящую из точек, равноу-

Свойства осевой симметрии

254  Свойства осевой симметрии. 

Свойства осевой симметрии 2

далениых от двух данных точек А и В, х
называют медиатрисой отрезка АВ.
Будем говорить, что отображение F является
инволюцией, если F2= Е. Легко видеть,
что если F — инволюция, тоF-1= F. о
У.3.1. Всякое инволютивное перемещение
F плоскости имеет хотя бы одну неподвижную
точку.
Д о к а з а т е л ь с т в о . Очевидно, Рис. 6
что для тождественного преобразования
плоскости (которое тоже есть инволюция) утверждение справедливо.
Пусть Рф Е. Тогда существует точка А плоскости, образ F(A)
которой (точка В) отличен от А. Так как F— инволюция, F (В)=
= F(F(A))=A. Отсюда следует, что образ отрезка А В при
перемещении F— отрезок АВ. Так как середина М этого отрезка—
единственная точка этого отрезка, равноудаленная от его концов,
a F сохраняет расстояния, то F (М) — I, т. е. М — неподвижная
точка F.
У.3.2. Любая осевая симметрия — инволюция.
Д о к а з а т е л ь с т в о . Пусть р — ось симметрии, ос — открытая
полуплоскость с границей р. При перемещении S2
P флаг
ОАа’, где [ОА) с: р, отображается на себя. Но существует единственное
перемещение, обладающее таким свойством (см. § 2). Очевидно,
что таким перемещением является тождественное преобразование,
т. е. 5р = Е.
Расстоянием между фигурами Фх и Ф2 (обозначается р (Ф1( Ф2)
называется точная нижняя грань множества \XY\, где X и V—
произвольные точки фигур Фх и Ф2:
р(Ф1( Ф2) = inf | XY |, где Х^Фх, Г^Фг
Расстояние определено для любых двух непустых фигур Фг
и Ф2, так как множество { | ХУ | : X € Фх, Y € Ф2} ограничено
снизу нулем. Однако не всегда существует такая пара точек Х0|
Y0, для которой р (Фи Ф2) = |Х0У0|.
Т е о р е м а 3.2. Для любой прямой р и точки X существует
единственная точка О прямой р, такая, что \ОХ\ = р (X, р).
Д о к а з а т е л ь с т в о . Теорема очевидна в случае X С р.
Пусть это не так (рис. 6). Образ точки X при симметрии Sp обозначим
через X’. Точки X и X’ разделены прямой р (У.2.1), причем
точка О — (XX’) П Р — середина отрезка XX’. Возьмем произвольную,
отличную от О точку М прямой р. Тогда точки М, X,
X’ не лежат на одной прямой и поэтому
\ХХ’\<\ХМ\ + \МХ’\. (1)
Но симметрия сохраняет расстояния. Значит, |ОХ| = |ОХ’|,
|МХ| =|УИХ’|. Из неравенства (1) получаем: 2 |0Х| <2 |УИХ|,
т. е. |ОХ|<|МХ|. Так как М—произвольная точка прямой р,
отсюда следует, что \ОХ\ = р (X, р).

255 Свойства осевой симметрии. 

Важным следствием доказанной теоремы является утверждение:
У.3.3. 1) Открытая полуплоскость является областью. 2) Граница
открытой полуплоскости ар — прямая р.
Прежде чем доказать это утверждение, напомним некоторые
определения. Множество Ф называется связным, если для любых
двух точек Ф существует отрезок или ломаная с концами в этих
точках, целиком содержащаяся в Ф. Точка X называется внутренней
точкой фигуры Ф, если существует круг с центром в этой
точке, целиком содержащийся в Ф; X — граничная точка Ф, если
всякий круг с центром X содержит как точки Ф, так и точки, не
принадлежащие Ф. Множество Ф называется открытым, если
всякая точка фигуры Ф — ее внутренняя точка. Множество граничных
точек Ф называется границей Ф. Открытое связное множество
называется областью.
Д о к а з а т е л ь с т в о . 1) Связность открытой полуплоскости
вытекает из аксиомы о разбиении плоскости прямой: отрезок,
соединяющий любые две точки ос’, содержится в а’р. Поэтому
остается доказать, что любая точка X Са’ является внутренней
точкой ос’, т. е. надо доказать, что для любой точки X £ ар существует
круг, содержащийся в а\
Обозначим расстояние р (X, р) через г. Тогда круг ^Х, не
содержит точки прямой р. Этот круг не содержит и точек из а’р:
если бы такая точка Y существовала, то отрезок XY пересекал бы
прямую р и, следовательно, круг |Х, yj содержал бы точку прямой
р.
2) Из проведенного только что рассуждения вытекает, что
точки открытых полуплоскостей а’р и а» не могут быть граничными
точками р. Остается показать, что любая точка прямой р — граничная
точка р. Это очевидно: как это следует из аксиом порядка,
на любой прямой, проходящей через М и пересекающей р (а значит,
и в любом круге с центром М), есть как точки из а’, так и
точки из ос».
Из предложения У.3.3 легко следует, что множество внутренних
точек угла (многоугольника) является областью и что граница
любого угла (многоугольника) есть объединение его сторон.
Т е о р е м а 3.3. Для любой прямой р и точки А, не принадлежащей
р, существует, и притом только.одна прямая, которая
проходит через точку А и при симметрии Sp отображается на
себя.
Д о к а з а т е л ь с т в о . Если прямая а проходит через точку
А и при симметрии Sp отображается на себя, то а содержит и точку
Sp (А). Так как по условию А £ р, то точки А и SP{A) различны.
Но через две точки проходит единственная прямая. Следовательно,
единственна и искомая прямая. Остается заметить, что прямая

256 Свойства осевой симметрии. 

Свойства осевой симметрии

при симметрии Sp отображается
на себя (Sp (Sp (Л)) = А, так как Sp —
инволюция).
Т е о р е м а 3.4. Если при симметрии
с осью р прямая а, отличная от р, отображается
на себя, то при симметрии
Sa прямая р также отображается на себя.
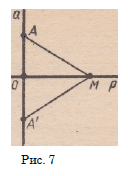
Д о к а з а т е л ь с т в о . Пусть Sp(a) —
= а и О = а[\р (рис. 7). Возьмем произвольную
точку М на прямой р, отлич- Рис. 7
ную от О. Допустим, что Sa (р) Ф р. Тогда
точка Sa (М) = М’ не лежит на прямой р и, значит, прямая
ММ’ пересекает а в некоторой точке Л, отличной от О. Как показано
в ходе доказательств теоремы 3.2, | АМ \ = р (М, а).
Так как Sp (а) — а и А ф О, то при симметрии Sp точка А
отображается на некоторую точку А’ £ а, отличную от А (эти точки
лежат по разные стороны от прямой р), причем \МА | = \МА’\
(симметрия сохраняет расстояния). Итак, на прямой а имеются две
точки А и А’, такие, что р(М, а) = \МА \ = \МА’\. Это противоречит
теореме 3.2.
В заключение параграфа докажем еще одну теорему.
Т е о р е м а 3.5. Всякое перемещение является композицией не
более трех осевых симметрий.
Д о к а з а т е л ь с т в о . Рассмотрим произвольное перемещение
F. Это перемещение вполне определяется указанием образов
трех неколлинеарных точек А, В, С (теорема 1.2). Пусть F (А)=А1,
F (В) = Blt F (С) = Сх. При доказательстве теоремы 2.1 мы показали,
что перемещение F’, отображающее А на Лх и В на Blf
представимо в виде композиции не более двух осевых симметрий.
Если F’ (С) = Сх, теорема доказана: F’ — F. Если F’ (С) ф Си
то F — композиция SAB °F’. Так как F’—композиция не
более двух осевых симметрий, теорема доказана.

257 Свойства осевой симметрии. 

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика.  Математика в школе.

Околоadmin