Углы

Углы

Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно: Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ ПЛОСКОСТИ И ЕЕ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. З. А. Скопец, Л. И. Кузнецова

(стр. 227-246)

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

§ 4. Углы.  А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.

В «Геометрии, 6—8» (п. 12) дается следующее определение:
«Объединение двух лучей с общим началом и одной из ограниченных
ими областей называется углом». Это определение предполагает,
что может быть доказана следующая теорема, из которой следует
существование углов.
Т е о р е м а 4.1. Любые два луча с общим началом разбивают
плоскость на две области. ,
Д о к а з а т е л ь с т в о . Требуется доказать два утверждения:
1) два луча с общим началом разбивают плоскость на два связных
подмножества Фх и Ф2; 2) каждое из этих подмножеств — открытое
множество. Докажем сначала первое из этих утверждений.
I. Доказательство проведем в несколько этапов.
1°. Если лучи ~р’0 и q’0 — противоположные лучи прямой р,
справедливость 1)—очевидное следствие теоремы 3.5: искомые
подмножества — открытые полуплоскости с границей р.
Отметим, что в этом случае оба угла со сторонами р’0 и q’0 —
выпуклые множества. Далее рассматриваются лучи р’0 и q’0, не содержащиеся
в прямой; при этом индекс «О» опускается.
2°. Из У.3.2 следует, что открытый луч р’ (и q’) содержится в одной
из открытых полуплоскостей с границей q (соответственно р).
Обозначим через а’ открытую полуплоскость с границей р, содержа-
§ 4. Углы
щую q , а через aq — открытую полуплоскость с границей q, со//
___ д»е ржиа щую рп’. Очевидно, что
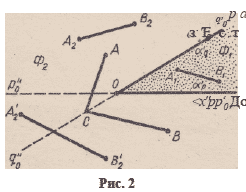
з Е с т е с т в е н н о предположить
(см* рис. 2), что искомые под-
множества Фх и Ф3 таковы:
п » н п
q, р a aq% q с= ар.
:»0 Естественно
<х»рр‘0 Докажем, что эти подмножества
действительно образуют разбиение
а У (р’ U</’) на два связных
подмножества.

Рис. 2
Очевидно, что {Фх, Ф2} —
разбиение множества точек пло-

242 Углы. 

скости, не принадлежащих р’ и q’. Кроме того, фигура Фх — пересечение
открытых полуплоскостей — выпукла. Поэтому отрезок,
соединяющий любые две точки Фх, содержится в Ф*, т. е. Фх —
связное множество.
Если точки А £ Ф2 и В £ Ф2 лежат в одной из открытых полуплоскостей
а» или oi”, то их также можно соединить отрезком,
содержащимся в а» (а»). Пусть Л £ а», но А $ а’; В £ а’ ,
но В $ а . Возьмем произвольную точку С открытого луча q»0
(рис. 2). Ломаная АС В соединяет точки Л и В и целиком содержится
в Ф2 (вследствие теоремы 3.1 ,[АС\ a aq, а [ВС\ с ар ).
3°. Итак, связность Фх и Ф2 доказана. Остается доказать, что
объединение этих фигур несвязно, т. е. надо показать, что любые
две точки, принадлежащие разным множествам Фх и Ф2, нельзя
соединить ломаной, не имеющей общих точек с лучами р’ и q’.
Покажем сначала, что если А £ Фх и В £ Ф2, то отрезок АВ имеет
общую точку либо с р’, либо с q’.
Если точка В принадлежит одной из открытых полуплоскостей
а’р или а’, то этот факт — очевидное следствие А.III.4 и У.З.2.
Пусть В £ ар П а». Так как точки Л и В лежат по разные стороны
от прямой р, отрезок АВ имеет общую точку М с прямой р.
Если М € р», то вследствие А.III.4 и У .3.2 отрезок МА, а значит,
и [АВ\ имеет общую точку с q . Перейдем к рассмотрению общего
случая. Пусть концы ломаной L = СХ С2 … Сп лежат в различных
множествах Фх и Ф2 (Сг £ Фх, Сп £ Ф2). Допустим, что L не имеет
общих точек с р’ U q’. Тогда [CiC2 ] f) L — [С2С3] f| L — ••• =
=[С„_1СЯ] П L=0. Из этих условий последовательно получаем:
С2 € Ф|, С3 ^ Фх, …, Сп £Фх (только что доказано, что если концы
отрезка лежат в различных множествах Фх и Ф2, то пересечение
этого отрезка с р’ (J q’ непусто). Получили противоречие с условием
Сп € Ф2.
II. Докажем теперь, что множества Фх и Ф2 открыты. Пусть,
например, X — произвольная точка Фх. Как показано при доказательстве
теоремы 3.5, существуют такие числа а и Ь, что расстояния
от X до прямых р и q равны а и Ь. Рассмотрим круг радиуса
г/2, где г — минимальное из расстояний а и Ь. Этот круг содержит
только точки Фх. Действительно, вследствие выбора г сразу получаем,
что этот круг не содержит точег^ прямых р и <7, а значит, и
лучей р’ и q’. Если бы существовала точка Y этого круга, лежащая
в Ф2, то отрезок XY, а значит и круг (О; г), как показано выше,
имел бы общую точку с р’ или q’.
От противного легко доказывается единственность разбиения
плоскости объединением двух лучей с общим началом на две области.
Между областями Фх и Ф2 (сохраняем обозначения, введенные выше)
есть важное различие: если р’ и q’ не содержатся в дрямой, то
Фх — выпуклая фигура, а Ф, — нет.

243 Углы. 

па овух иилистеи, ограниченных
двумя лучами с общим
началом, не содержащимися
в прямой, только одна — фигура
выпуклая.
Д о к а з а т е л ь с т в о .
Выпуклость Фх уже отмечалась
выше. Покажем, что в Ф2 найдутся
две такие точки С и D, что
[С/)]д£Фа. Пусть A ZjS, B^cf.
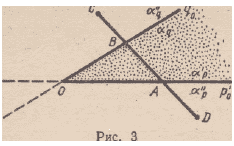
Выберем на луче АВ такую точку С, что \АС\ > \АВ\\ на луче
В А — точку D; \BD\>\AB\ (рис. 3). Тогда А и С разделены прямой
q, а точки В и D — прямой р. Но Л € а’я, В £ а’р. Значит,
С £ al, D £ ар. Внутренние точки отрезка АВ принадлежат от
резку CD. Следовательно, отрезок CD не является подмножеством
Ф2, хотя его концы лежат в Ф2.
Доказав теорему 4.1, мы доказали законность определения угла,
имеющегося в «Геометрии, б—8». Каждый угол является либо
полуплоскостью, либо пересечением, либо объединением двух
полуплоскостей, границы которых пересекаются. Соответственно
этому будем различать развернутые, выпуклые и невыпуклые углы.
(Строго говоря, развернутые углы следовало бы также называть
выпуклыми углами: полуплоскость — фигура выпуклая. Однако
имеется целый ряд особенностей, выделяющих развернутые углы
среди других углов. Так, для развернутых углов вершины и стороны
определяются неоднозначно; предложения У.4.1 и У.4.2 не-,
верны, если под выпуклыми углами понимать и развернутые. По-
видимому, для удобства речи, чтобы избежать частого употребления
оговорок «выпуклый угол, отличный от развернутого», естественно
различия, существующие между развернутыми и другими
выпуклыми углами, следует отразить в терминологии, что и сделано
в настоящей работе.)
Лучи ро и q’o называют сторонами двух углов, которые эти
лучи определяют; точка О — вершина каждого из этих углов. Точки
угла, не принадлежащие его сторонам, называют его внутренними
точками, а точки сторон — его граничными точками (нетрудно проверить,
что внутренние и граничные точки удовлетворяют определениям,
данным на стр. 230).
У.4.2. Если открытый луч р’о содержит внутреннюю точку угла
АОВ, то каждая точка р’о — внутренняя точка угла АОВ.
Это утверждение — очевидное следствие У.3.2.
Т е о р е м а 4.2. Луч с началом в вершине выпуклого угла
Z-p’q’, содержащийся в Z.p’q’ и отличный от сторон этого угла,
пересекает любой отрезок с концами на лучах р’ и q’ во внутренней
точке этого отрезка.
Д о к а з а т е л ь с т в о . Пусть А а В — концы данного отрез

244 Углы. 

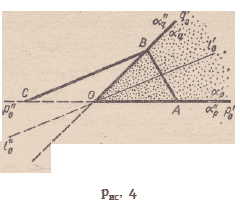
ка, причем А £ р’о, В £ q’0 (рис.
4), 10 — данный луч. Возьмем
произвольную точку С на р’о•
Применяя теорему Паша, получаем,
что / имеет общую точку
с [АВ] или с [ВС].
Отрезок ВС и прямая I не
имеют общей точки: [ВС] а а»„ П
Следовательно, прямая I пере- Чо/
секает отрезок АВ. l’o и [ЛВ] рис, 4
не имеют общей точки: Г0 с а»,
[ЛВ] с ар. Остается заметить, что, поскольку l’o лежит внутри
угла ЛОВ, точка пересечения l’o с отрезком Л В отлична от Л и В.
Т е о р е м а 4.3. Если выпуклые углы аир имеют общую вершину,
а стороны а содержатся в угле р, то угол а — подмножество
р.
^ Д о к а з а т е л ь с т в о . Рассмотрим сначала частный случайна
и Р_имеют общую сторону. Докажем, что в этом случае
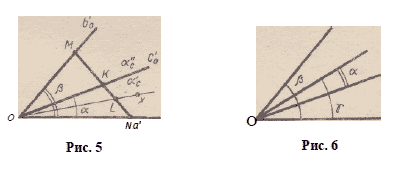
Z.a’c’ cz Z.a’bS (рис. 5). Для этого возьмем точки М и N на сторонах
угла Z-a’b’. Пусть X— произвольная внутренняя точка угла
Z_a’с’. Все точки луча ОХ, кроме О, —внутренние точки Z.a’с'(У.4.2).
Так как по условию луч с’ лежит внутри Z-a’b’, с’ пересекает отрезок
MN в некоторой точке К, (теорема 4.2). Точка пересечения
L луча ОХ с отрезком KN — внутренняя точка Z-a’c’.
Так как L £ [/(W1, отрезок KL — подмножество отрезка MN.
Но L £ Z-a’b’. Следовательно, луч ОХ — подмножество Z-a’b’
(УЛ.2). В частности, X € Z-a’b’. Но X — произвольная точка
Z.a’c’. Значит, Z-a’c’ cz Z-a’b’.
Очевидно, что имеет место строгое включение. Например, внутренние
точки отрезка МК не принадлежат ZLa! с’\ точки М и L
разделены прямой с. Значит, М £ Z-a’b’, но М £Z.a’c’.

245 Углы. 

Теперь доказательство в общем случае получается просто (рис. 6).
Применяя дважды уже полученный результат, имеем:
Z.acrZ-6) }=±>Z. — acrZ.8. „.
В заключение напомним определение суммы углов: объединение
двух углов с общей вершиной называется суммой этих углов, если
их пересечением является луч. Отметим, что сумма углов определена
не всегда.
С доказательством теорем § 4 в целом завершается работа по
выводу недоказанных в школьном курсе предложений на основе
системы аксиом, сформулированной в «Приложениях» к учебнику
геометрии для 6—8 классов. Отметим, что сформулированная выше
аксиома A.III.4 отличается от соответствующей аксиомы о разбиении
плоскости (см. теорему 3.5), имеющейся в школьном курсе.
Доказав с помощью аксиомы A.III.4 теорему 3.5, мы показали,
что, постулируя свойства плоскости, можно отказаться от требования,
чтобы каждая точка «открытой полуплоскости» была ее внутренней
точкой.

246 Углы.

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика.  Математика в школе.

Углы