§ 14. Умножение нескольких чисел и возведение отрицательного числа в степень.
Глава II. Положительные и отрицательные числа.
На главную страницу Алгебра. Д.К. Фаддев, И.С. Соминский.
Скачать оригинал Алгебра. Д.К. Фадеев, И.С. Соминский на странице Сборники Математики.
Ниже можете посмотреть тексты для быстрого ознакомления (формулы отображаются не корректно).
Похожие статьи: Алгебра в школе. ЕГЭ 2015 Математика. Библиотека учителя. Школьная математика.
Купить книги по математике за низкие цены:
П р и м е р . (—5) • 4 • (—3) • 2 . (—0,5) • (—3).
Р е ш е н и е . Выполняем умножение, последовательно присоединяя
множители по одному. Получим
(—5) • 4 = —20; (—20) • (—3) = 60;
60 . 2 = 120; 120 • (—0,5) = —60; (—60) • (—3) =180.
Итак,
(—5) • 4 . (—3) • 2 • (—0,5) • (—3) = 180.
Ответ. 180.
На каждом шагу приведенного вычисления мы умножаем абсолютную
величину предшествующего результата на абсолютную величину
присоединенного множителя. Поэтому абсолютная величина произве?
дения нескольких чисел равна произведению абсолютных величин
сомножителей.
Далее, на каждом шагу знак результата совпадает со знаком предшествующего
результата, если присоединяется положительный множитель,
и знак последующего результата противоположен знаку предшествующего,
.если присоединяется отрицательный множитель. Поэтому
произведение нескольких чисел положительно, если все сомножители
положительны или если число отрицательных сомножителей
четно. Если же число отрицательных сомножителей нечетно,
то произведение отрицательно.
Таким образом, мы пришли к следующему правилу умножения нескольких
чисел:
67 Основное свойство нуля.
П р а в и л о . Чтобы перемножить несколько чисел, нужно перемножить
их абсолютные величины и взять результат со знаком
если число отрицательных сомножителей четно, или со
знаком — , если число отрицательных сомножителей нечетно.
Заметим, что если хотя бы один из сомножителей равен нулю,
то и произведение равно нулю.
Из правила умножения нескольких сомножителей вытекает следующее
правило для возведения отрицательных чисел в степень:
П р а в и л о . При возведении отрицательного числа в степень
с четным показателем результат положителен. При возведении
отрицательного числа в степень с нечетным показателем результат
отрицателен. Абсолютная величина степени равна степени
абсолютной величины основания с тем же показателем. Например,
(—2)в = —32; (_3)* = 81;(-f)3 = -^.
Действительно, степень отрицательного числа есть произведение
равных ему сомножителей, число которых равно показателю степени.
Если показатель степени есть четное число, то результат положителен,
если показатель степени есть нечетное число, то результат отрицателен.
Абсолютная величина степени равна произведению сомножителей,
каждый из которых равен абсолютной величине основания, т. е. равна
степени абсолютной величины основания с тем же показателем.
Отметим одно важное следствие: степень с четным показателем
любого рационального числа не отрицательна. Это можно записать
так: при любом а и при любом натуральном числе п
a2nSzO.
Действительно, любая степень положительного числа есть положительное
число, любая степень числа 0 равна 0, и, наконец, степень
с четным показателем отрицательного числа есть число положительное.
В частности, не существует числа, квадрат которого был бы
равен отрицательному числу.
Упражнения
68 Основное свойство нуля.



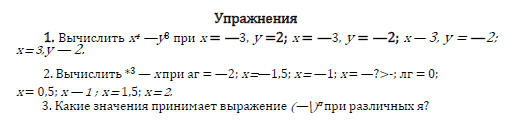


Comments