2. ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА.

Текст просто для быстрого ознакомления с темой в общих чертах (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):

1. В кабинете должны быть также и демонстрационные р у с-
ск.ие с ч е т ы . Русские счеты, входящие в набор наглядных пос
о б и й средней школы, давно уже утратили былое значение
универсального счетного устройства: их место на столе бухгалтера
занял арифмометр. И в школе они используются не как
вычислительный прибор, а как дидактический материал при
изучении десятичной системы счисления в младших классах.
Счеты оказываются незаменимым пособием и при изучении
иных позиционных систем счисления, которые с каждым годом
занимают все более прочное место в программах школьных математических
кружков, а теперь введены в план факультативных
занятий по математике для VII класса.
Для занятий со счетами по недесятичной системе счисления
приходится изменять число косточек на каждой спице. Если основание
системы меньше десяти, то удобно пользоваться картонной
(а еще лучше металлической) маской, закрывающей все
неиспользуемые косточки счетов. Для этого маска должна иметь
длину, покрывающую все спицы счетов, и ширину, покрывающую,
например, восемь косточек каждой спицы. Маска должна
быть снабжена двумя полями, отогнутыми под прямым углом
к ней. В полях делаются прорези для спиц, позволяющие надеть
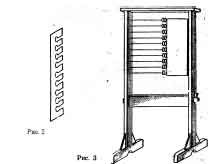
маску на счеты (рис. 2).
• Для работы с двоичными числами маска должна закрыть
по восемь косточек каждой спицы с правой стороны счетов. Правое
поле маски, обращенное к двум незакрытым косточкам, выполняет
роль борта счетов при работе с этими косточками
(рис. 3). Опишем методику работы с двоичными счетами.

37 ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА. 

ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА 

Учитель напоминает, как пользоваться десятичными счетами,
предлагая ученикам сосчитать на счетах до двадцати. Отсчет
ведется на открытых счеггах (без маски).
Отмечается, что положение, когда на одной из спиц отложены
все косточки, является неправильным. Приводятся три-
четыре примера записи чисел, отложенных на счетах; число косточек
на каждой спице отмечается цифрой, положение спицы
(ее номер) —положением цифры.
Теперь счеты закрывают маской. Учитель опрашивает,
можно ли считать на таких счетах, у которых на каждой спице
всего по две косточки. Он начинает счет: на первой спице откладывает
одну косточку (один), затем вторую (два). Но такое
положение счетов неправильное. Учитель сбрасывает отлож-ен-
ные косточки, заменяя их одной косточкой второй спицы. Так
ведется счет до восьми или до шестнадцати. Затем ставится во*
прос: как прочесть отложенное на счетах число (например,
10112=11ю)? Однако оказывается, что эта задача вызывает затруднение.
Тогда учитель предлагает сделать облегчающие чте-
— ние надписи.
Снова ведется счет от единицы. На маске появляются числа,
надписываемые мелом против спиц в тот момент, когда счет
доходит до этих спиц: 2, 4, 8, 16, 32, 64, 128……… (Мы пользовались
счетом именно до 128 — атого вполне достаточно. Если
на счетах используются и спицы, расположенные выше восьмой,
то их обозначают следующими степенями двоек уже без непосредственного
счета.)
В процессе счета до 128 можно сбиться. Тогда уже имеющиеся
надписи помогут исправить ошибку. Пусть, например»

38 ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА. 

уже поставлены числа против первых шести спиц: 1, 2, 4, 8, 16,
32. При счете мы сбились и не помним, отложено ли у нас число
45 или 46. Подсчитываем это число по положению косточек.
Пусть на первой спице отложена одна косточка, на второй —
ничего, на третьей — одна (это число 4), на четвертой — одна
(это число 8), «а пятой —ничего, на шестой — одна (это число
32). Сложив 1+4+8+32, убеждаемся, что мы отсчитали 45.
(Заметим, что четность числа устанавливается по одному только
состоянию первой спицы — спицы единиц.)
Такие подсчеты очень нужны как тренировка перевода
двоичного числа в десятичное, и учитель во время счета должен
часто их проводить.
Итак, маска размечена, учащиеся получили некоторый опыт
работы со счетами в двоичной системе, научились читать двоичные
числа, отложенные на надписанных счетах. . .
Теперь нужно научить более трудному приему — установке
на счетах в двоичной системе заданного десятичного числа.
Предлагаем ученикам отложить такие числа:
а) 2, 8, 16, 1, 32, 64, 128, 4;
б) 3, 9, 17, 33, 65, 129, 5;
в) 6, 12, 20, 5, 35, 68, 132; *
г) 35, 47, 17, 63, 122, 15, 127……….
Задачи пункта г) (т. е. задачи на установку произвольно
выбранного числа, в отличие от специально ‘подобранных, легких
задач первых трех пунктов) нужно решать до тех пор, пока
каждый ученик не усвоит методику их решения, заключающуюся
в последовательном вычитании из заданного числа степеней
числа два. Например, для установки числа 122 нужно учесть,
что старшее из чисел, проставленных на маске, не превышающее
числа 122, есть число 64. Откладываем 64. Осталось отложить
122—64=58. Теперь откладываем 32. Осталось отложить
58—32 =’26. Отложим 16. Осталость отложить 26—16=10. От*
кладываем 8. Осталось отложить 10—8=2. Отложим 2. Работа
окончена: 12210=1 111 010г.
Далее ставится и решается задача об угадывании (в шесть
вопросов) любого чвсла от одного до шестидесяти трех. На вопросы
можно отвечать либо «да», либо «нет». Первое число отгадывает
учитель. Он становится у доски, отвернувшись от счетов,
и предлагает кому-либо из учеников отложить на счетах
задуманное число, меньшее шестидесяти четырех. Ученик делает
это под контролем всего класса. Затем учитель спрашивает:
«Есть ли единица на щестой спице?» Если да, учитель пишет на
доске единицу, если нет — пишет нуль. Второй вопрос: «Есть ли
единица на пятой спице?» И после шести вопросов на доске оказывается
написанным число в двоичной системе. Учитель переводит-
его в десятичную систему. Задача решена.
Потом отгадывают числа учащиеся. Смысл заключается в
том, что ученики в ходе этой игры обучаются записи двоичных

39 ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА. 

чисел. При этом им предлагается всегда пользоваться индексом
— указателем системы счисления, (опуская его лишь для
десятичных чисел: 10002=8.
Дальнейшая работа с двоичными числами — разъяснение
математической сущности записи числа с помощью степеней
двойки и сравнение с записью с помощью степеней десяти —
идет без использования счетов.
Счеты привлекаются вновь при сложении и вычитании двоичных
чисел. Эта работа на счетах ведется до введения таблицы
сложения:
+ 1 0 1
0 10 1
ill 10
Каждый ученик должен на счетах сделать хотя бы по одному
примеру на сложение и вычитание двоичных чисел. В отличие
от сложения и вычитания столбиком работа на счетах ведется
начиная со старших разрядов (так же, как и при работе на
счетах в десятичной системе).
Счеты с надписанной маской должны быть перед глазами
учеников в течение всей работы с двоичными числами как хорошая
подсказка при переводе чисел из двоичной системы «в десятичную
и обратно.
Аналогично используются счеты и при изучении других систем
счисления: троичной, восьмиричной и т. д. При желании
показать ученикам систематические числа с основанием более
десяти имеет смысл добавить косточки на спицах, снимая их для.
этого с других спиц. •
Учитель может использовать счеты и для работы с систематическими
дробями при любом основании.
2. Русские счеты наглядно (изоморфно и просто) интерпретируют
позиционный принцип, суммирование чисел и нахождение
разности чисел. Умножение и деление на счетах выполняются
особыми приемами, не являющимися объектом изучения
в школе. На а р и ф м о м е т р е, напротив, сложение и вычитание
выполняются не наглядно: виден лишь результат. Зато умножение
и деление на арифмометре выполняются как последовательное
сложение и вычитание. Тем самым наглядно интерпретируются
известные школьнику определения и алгоритмы. Опыт показывает,
что даже небольшое число упражнений с арифмометром
резко повышает вычислительную культуру школьника. Это
и понятно: арифмометр овеществляет те умственные действия,
которые школьник часто выполняет не очень сознательно. Поэтому
мы и настаиваем на необходимости иметь арифмометр в
школьном кабинете. К работе на нем необходимо привлекать
школьников, которые плохо справляются с умножением и делением
чисел.

40 ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА. 

3. Организация работы учащихся с л о г а р и ф м и ч е с
к о й л и н е й к о й оставляет пока что желать лучшего. Учитель
использует демонстрационную линейку обычно только при
изучении специальной темы «Логарифмическая линейка». Нечего
и думать о том, что при такой постановке дела ученики приобретут
прочный навык пользования этим инструментом. Логарифмическую
линейку следует использовать при всяком удобном
случае. Например, решение большинства вычислительных
задач о подобных треугольниках производится одной установкой
движка. Во время изучения темы «Подобие» демонстрационная
логарифмическая лйнейка и индивидуальные линейки у
учащихся должны использоваться постоянно. То же нужно сказать
и о таких вопросах, как решение треугольников, измерение
площадей и объемов, прогрессии, извлечение корней и т. д. Гораздо
шире следует пользоваться линейкой и при работе с логарифмами.
Вообще логарифмической линейкой нужно пользоваться
во всех случаях, в которых используются четырехзначные
таблицы, и не реже, чем этими таблицами.
Приведем пример решения задачи о подобных треугольниках
при помощи логарифмической линейки.
З а д а ч а . Периметр треугольника равен 257 ед. Стороны
подобного ему треугольника равны соответственно 36,7 ед.,
45.8 ед. и 49,0 ед. Найти длины сторон первого треугольника.
Р е ш е н и е . Периметр второго треугольника, как нетрудно
убедиться, равен 131,5 ед. Условимся располагать данные о первом
треугольнике на основной шкале линейки, а данные о втором
треугольнике —на движке. Установим число 131,5 на движке
против числа 257 » основной шкалы линейки. Тогда против
значений длин сторон второго треугольника (движок) окажутся
значения длин сторон первого треугольника. Читаем ответ:
71.8 ед., 85,9 ед., 95,8 ед. Разумеется, в иных случаях решение
треугольника привело бы к необходимости переброски движка.
Такая необходимость исчезает, если решать задачу на шкале
квадратов (с некоторой потерей точности). Отметим, что при
решении мы производили подряд два действия: деление и умножение.
В частности, единица движка указывала результат деления
257 на 131,5. Это 1,955 — коэффициент подобия треугольников.
‘
Серьезное неудобство при изучении логарифмической линейки
состоит в том, что деления демонстрационной линейки не
видны не только с последних, но даже и со средних парт в классе.
Устранить этот недостаток практически невозможно: линейку
пришлось бы делать слишком больших размеров. Выход из
этого положения найден в создании серии диапозитивов «Работа
на логарифмической линейке», выпускаемой студией «Диафильм
». В серии 10 кадров, в них показаны всё изучаемые в
школе действия на линейке. В кадрах на экране хорошо видны
деления.

41 ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА. 

4. Для того чтобы добиться уверенной и быстрой работы на
логарифмической линейке, нужно правильно организовать, ее
изучение. В частности, навыки чтения шкалы и работы с движком
и визиром можно, начать отрабатывать задолго до изучения
логарифмической линейки — на линейке арифметической.
А р и ф м е т и ч е с к а я л и н е й к а может использоваться начиная
с I класса, своевременно заменив собой счетные палочки.
Вначале используется только одна шкала линейки — числовой
луч, затем вводится и вторая. На протяжении первых четырех
лет обучения в школе ученики смогут освоиться с чтением шкалы
и приучиться к работе с движком и бегунком. Арифметическая
линейка изготовляется с помощью наложения новых шкал
на логарифмическую линейку. Новые шкалы удобно сделать из
миллиметровки и наклеить на линейку клеем, не портящим линейки
и легко смываемым (например, казеиновым канцелярским
клеем). Это относится и к демонстрационной, и к индивидуальным
линейкам. Понятно, что в кабинете-придется иметь
два их комплекта.
Вначале, в I классе, можно использовать только пару основных
шкал линейки (остальные шкалы нужно заклеить чистой
бумагой, чтобы они не мешали). На этих шкалах ученики
будут считать до IV класса включительно. Они особенно понадобятся
при действиях с десятичными дробями. Затем в V классе
понадобится еще одна пара шкал’для действий с отрицательными
числами. Для -этого используются самодельные шкалы,
наклеенные на шкалы квадратов логарифмической линейки.

42 ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА.

Задачи Школьной математики.
Для учителей Математики в школе.

Околоadmin