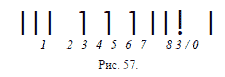Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ(стр. 71-75)
Текст для быстрого ознакомления:
X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ
118. Записать единицу тремя пятерками
Пользуясь тремя пятерками и какими угодно знаками
математических действий, написать выражение,
равное единице.
Если вы никогда не пробовали решать подобные
задачи, то вам немало придется подумать, прежде
чем вы нападете на правильное решение. Вот одно
решение предлагаемой задачи: 1 = , Попробуйте
найти другие решения.
*) Кость — это кубик, на каждой из шести граней которого
написано по одной цифре от 1 до 6,
71 X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ
———————————————————————————————————————————————
Скачать бесплатные книги — Математика, Физика, Словари, Брокер, МЛМ, Колледж онлайн, Косметика.
Научитесь раскручивать свои сайты бесплатно!
———————————————————————————————————————————————
119. Записать двойку тремя пятерками
Как записать двойку тремя пятерками?
120. Записать четыре тремя пятерками
Как записать четыре тремя пятерками?
121. Записать пять тремя пятерками
Как записать пять тремя пятерками?
122. Записать нуль тремя пятерками
Как записать нуль тремя пятерками?
123. Записать 31 пятью тройками
Как записать 31 пятью тройками?
124. Автобусный билет
В автобусе вам попался билет с номером 524127.
Попробуйте, не меняя порядка цифр, расставить
между ними знаки математических действий так, чтобы
в итоге получилось 100.
Эта занятная игра может скрасить вам время
длительной поездки, если вы попытаетесь получить
100 подобным же образом из номера попавшегося
вам билета. Если вы едете не одни, то можно устроить
маленькое соревнование: кто быстрее получит
100 из цифр своего билета.
125. Кто первый скажет «сто»?
Двое поочередно называют произвольные числа,
ке превышающие 10. Эти числа складываются одно
за другим, и выигрывает тот, кто первый достигнет
ста.
Если первый скажет, например, «7», а второй
«10», получится «17»; затем первый говорит, например,
«5», получится «22»; второй говорит «8», получится
«30» и т. д. Победителем будет тот, кто первый
получит «100».
Как сделать так, чтобы наверняка первьш сказать
«сто»?
72 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ
126. Обобщение
Предыдущую задачу можно предложить и в таком
общем виде.
Двое называют поочередно произвольные числа,
не превышающие, однако, какого-нибудь условленного
предела. Эти числа складываются одно за другим,
и выигрывает тот, кто первый достигает какого-
нибудь заранее назначенного числа.
Сделать так, чтобы первым прийти к этому назначенному
числу.
127. Собрать в группы по 2
Десять спичек положены в один ряд (рис. 57).
Требуется распределить их попарно, всего в 5 пар,
перекладывая по одной спичке через две (например,
первую переложить к четвертой).
128. Собрать в группы по 3
Пятнадцать спичек расположены в ряд. Требуется
собрать их в 5 кучек по 3 спички, перекладывая
их по одной, и каждый раз перескакивая при этом
через 3 спички.
129. Детская пирамида
Возьмем 8 деревянных или из толстого картона
кружков уменьшающегося диаметра и 3 вертикально
укрепленные на подставках палочки (стержня).
Кружки снабжены в центре отверстиями, и их накладывают,
начиная с наибольшего, на одну из палочек
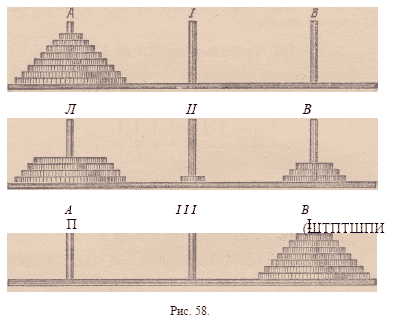
А Это и есть детская пирамида в 8 этажей (рис. 58,
вверху).
Требуется эту пирамиду с палочки А перенести
на палочку В, пользуясь третьей палочкой (I, II и
III на нашем рисунке) как вспомогательной и соблюдая
следующие условия: 1) не переносить за один
раз более одного кружка, 2) класть снятый кружок
73 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ
или на ту палочку, которая свободна, или накладывать
его на кружок большего диаметра. Надевать на
какую-либо из палочек больший кружок поверх
меньшего нельзя.
Л е г е н д а . Если выше вместо 8 кружков возьмем
64 кружка, то получим задачу, связанную с
древнеиндийской легендой. Легенда эта гласит, будто
в городе Бенаресе, под куполом главного храма, в
том месте, где находится середина Земли, бог Брама
поставил вертикально на бронзовой площадке три
алмазные палочки, каждая длиною в локоть и толщиною
в корпус пчелы. При сотворении мира на одну
из этих палочек были надеты 64 кружка из чистого
золота с отверстиями посередине — так, что они образовали
род усеченного конуса, так как диаметры
их шли в возрастающем порядке, начиная сверху.
Жрецы, сменяемые один другим, днем и ночью без
устали трудятся над перенесением этой колонны
кружков с первой палочки на третью, пользуясь второй
как вспомогательной, причем они обязаны соблюдать
условия, т. е. 1) не переносить за один раз
более одного кружка и 2) класть снятый кружок
74 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ
или на свободную в этот момент палочку, или накладывать
его на кружок только большего диаметра.
Когда, соблюдая все эти условия, жрецы перенесут
все 64 кружка с первой палочки на третью, наступит
конец мира…
130. Интересная игра
Попробуйте со своим товарищем сыграть в следующую
игру. Разложите на столе три кучки спичек.
Например, в 12, 10 и 7 спичек. Игра заключается в
том, чтобы поочередно брать из кучек некоторое, какое
вам захочется, количество спичек, но каждый
раз только из одной кучки. Можно взять и сразу целую
кучку. Выигрывает тот, кто последним возьмет
спички, Давайте для примера разыграем партию.
Одного игрока обозначим Л, другого Б.
Исходное положение 12, 10, 7
После хода А 12, 10, 6
» Б 12, 7, б
» » А * ) 7, 6
» » Б * * 5, 6
» » А * ! 5, 4
» » Б * ) 3, 4
» » А 3, 2
» » Б 2, 2
» » А 0, 2, 2
» » Б о, 1, 2
» » А 0, 1, 1
» Б о, 0, 1
Последним ходом игрок А выигрывает. Вопрос
состоит в следующем: может ли А играть так, чтобы
всегда выигрывать?
75 Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. Школьные задания по математике. X. ИГРЫ С ЧИСЛАМИ И ПРЕДМЕТАМИ.