Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИЙ.
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИЙ.(стр. 180-185)
Текст для быстрого ознакомления:
Путешествие по стране геометрии. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
XV. ГЕОМЕТРИЯ ПУТЕШЕСТВИЙ.
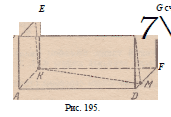
167. С первого взгляда кажется ясным, что паук должен
пробежать потолок по диагонали СЕ и затем спуститься к мухе
по ребру ЕК.
Поразмыслив, мы найдем для паука и другой путь: он может
пробежать боковую стену по диагонали CF и подобраться
к жертве по F K .
И, наконец, паук мог бы пойти по СЛ и по Л/С.
Параллелепипед симметричен относительно середины диагонали
С К , поэтому каждый из путей CDK, СВК и CGK равен по
длине одному из трех приведенных выше путей.
Какой же из них является кратчайшим?
Оказывается, что ни тот, ни другой, ни третий. Есть еще
более короткие пути, займемся их разысканием.
Ввиду симметрии параллелепипеда можно считать, что кратчайший
путь паука не заходит на боковую стену ЛВЕК. Действительно
(рис. 195), например, длина пути KLC равняется длине
мы ясно видим, что пути СЕК и CGK, казавшиеся нам в неразвернутом
чертеже кратчайшими, на ‘самом деле таковыми не являются.
Стоит соединить точки С и К прямой линией, чтобы получить
заметно более короткий путь. Этот путь будет кратчайшим
среди всех путей, пересекающих ребро EG. Аналогично, путь
КС2 будет кратчайшим среди всех путей, пересекающих ребро
FD (точка С2 также отвечает вершине С нашего параллелепипеда).
В частности, он будет короче пути CFK.
Для того чтобы представить себе кратчайший среди путей,
пересекающих ребро GF, развернем комнату, как показано на
рис. 197. Мы видим, что КСз— кратчайший из путей, пересекающих
ребро GF.
Остается теперь решить вопрос: какой же из этих трех путей
( К С , КС2, KCs) будет самым коротким. Оказывается, что это
зависит от относительных размеров комнаты в длину, ширину и
высоту.
Обозначим длину комнаты AD через а, высоту А В через b
и ширину А К через с. Тогда из рис. 196 и 197 имеем
пути КМС. Поэтому можно
Е G считать, что путь пересекает 7\ одно из ребер EG, GF, FD,
AD. Ввиду симметрии ребер
AD и EG достаточно считать,
что он пересекает EG,
GF или FD.
Рис. 195.
F Развернем параллелепипед,
изображающий нашу
комнату, на плоскость. Получим
чертеж, представленный
на рис. 196.
Паук сидит в точке С,
а муха — в точке К. Теперь
I КС I = Уа2 + (Ь + с ) 2 .
\ К С 2 \ = У ( а + W + с 2 .
| К С 3 1 = V ( а + с ) 2 + ¥ .
180 Путешествие по стране геометрии. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
Раскрывая скобки и сравнивая между собой подкоренные
выражения, мы видим, что они отличаются друг от друга лишь
членами
2 Ьс, 2 ab, 2 ас.
Деля все три произведения на 2abc, получим
JL -L _L
а9 с’ Ь •
Отсюда видно, что если
а > 6, а> с,
то кратчайшим путем будет путь КС\ если
с > а, с > Ъ,
то кратчайший путь КС2\ если же
b > а, b > с,
то кратчайший путь КСз.
Мы видим, что кратчайший путь паука должен пересекать
самое длинное из ребер
EG, GF, FD.
Задача о пауке и мухе оказалась гораздо сложнее, чем
можно было думать с первого взгляда.
169. Имеется только две нечетных местности D и Е. Все
остальные местности четные. Из общих рассуждений перед уело*
вием задачи следует, что она разрешима.
Кроме того, мы знаем, что обход должен начаться из нечетной
местности D или Е.
Искомый обход мостов может быть сделан так:
EaFbBcFdAeFfCgAhCiDkAmEnApBqElD,
или в обратном порядке. Маленькие буквы среди больших показывают,
какие именно переходятся мосты.
170. Исследуя разрешимость задачи, сразу видим, что Финляндия,
Испания и Дания имеют нечетное число границ с соседними
государствами, т. е. число нечетных местностей более двух.
А следовательно, путешествие, которое предполагает совершить
контрабандист, невозможно.
171. См. рис. 198.
172. Изобразим каждого рабочего и каждый станок на листе
бумаги в виде точки. Всего получится 20 различных точек. Проведем
теперь из каждой точки, изображающей рабочего, две линий
к точкам, изображающим станки, на которых этот рабочий
умеет работать. Мы получим сеть, состоящую из 20 точек и 20 линий,
причем из каждой точки, вне зависимости от того, соответствует
она рабочему или станку, выходят две линии.
Получившаяся сеть распадается на несколько кусков таких,
что в пределах одного куска можно пройти по линиям сети от
182 Путешествие по стране геометрии. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
183 Путешествие по стране геометрии. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
184 Путешествие по стране геометрии. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.
каждой точки до любой другой. Если же точки принадлежат
разным кускам, то не существует пути, соединяющего их.
Так как в каждом куске сети все вершины четные, то его
можно вычертить одним росчерком. Расставим на каждой линии
сети стрелочки в соответствии с направлением вычерчивания.
Тогда из каждой точки сети будет выходить единственная линия.
Линия, выходящая из точки, изображающей рабочего, будет
входить в точку, изображающую станок, на котором этот рабочий
будет работать.
Утверждение остается верным, если число Ю в условии задачи
заменить любым другим целым числом, не меньшим 2. Решение
остается тем же самым.
185 Путешествие по стране геометрии. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ.