Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ.
Математика для младших классов.
ХIII. ШАХМАТЫ
Скачать бесплатно Ё. И. ИГНАТЬЕВ «В ЦАРСТВЕ СМЕКАЛКИ» в формате PDF в хорошем качестве. Вся книга.
Скачать бесплатно Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика для младших классов. ХIII. ШАХМАТЫ (стр. 82-123)
Текст для быстрого ознакомления:
ХIII. ШАХМАТЫ
ШАХМАТЫ в математике
По поводу 20-значного числа, приведенного в решении
задачи 129 существует другая легенда, тоже
индусского происхождения, которую рассказывает
арабский писатель Асафад
Брамин Сесса, сын Дагера, придумал игры в шахматы,
где король, хотя и самая важная фигура, не
может ступить шагу без помощи и защиты своих подданных
пешек и других фигур. Изобрел он эту игру в
забаву своему монарху и повелителю Индии, Шера-
ну. Царь Шеран, восхищенный выдумкой брамина,
сказал, что даст ему все, что только брамин захочет.
— В таком случае,— сказал Сесса,— прикажи
дать мне столько пшеничных зерен, сколько их получится,
если на первую клетку шахматной доски положить
зерно, на вторую 2, на третью 4, на четвертую
8 и т. д., все удваивая, пока не дойдут до 64-й
клетки.
Повелитель Индии не смог этого сделать. Число
требуемых зерен выражалось двадцатизначным числом.
Чтобы удовлетворить «скромное» желание брамина,
нужно было бы восемь раз засеять всю поверхность
земного шара и восемь раз собрать жатву,
Тогда бы только получилось нужное для Сессы количество
зерен.
Обещать «все, что хочешь», легко, но трудно ис- 4
полнить!
83 ШАХМАТЫ в математике
146. Четыре коня
На шахматной доске стоят 4 коня (рис. 66). Требуется
разделить доску на 4 одинаковые по форме
части, на каждой из которых стоял бы в точности
один конь.
84 ШАХМАТЫ в математике
147. Пешка и конь
Поставим на шахматную доску пешку. Может ли
конь, помещенный на одну из свободных клеток, обой^
ти все остальные клетки и вернуться на исходную, побывав
на каждом свободном поле только один раз?
148. Две пешки и конь
Поставим две пешки в противоположные углы
шахматной доски. Может ли конь обойти оставшуюся
часть доски так, как это требуется в предыдущей
задаче?
149. Конь
Может ли конь обойти 16 центральных полей шахматной
доски, побывав на каждом поле по одному
разу?
150. Жуки
Представьте себе, что вам удалось поймать 25 жуков
и рассадить их по одному на каждой клетке куска
шахматной доски размером 5X5 (рис. 67). Да-
вайте предположим теперь, что каждый жук переполз
на соседнюю по горизонтали или вертикали
клетку этого куска доски. Как вы думаете, останутся
ли при этом пустые клетки?
151. Жуки на шахматной доске
Каков будет ответ на вопрос предыдущей задачи
для всей шахматной доски размером 8X8?
85 ШАХМАТЫ в математике
152. Замкнутый путь жука
Может ли жук, помещенный на некоторую клетку
шахматной доски, переползая на соседние клетки по
горизонтали или вертикали, обойти всю доску и вернуться
на исходную клетку, побывав при этом на
каждой клетке только один раз?
153. Пешка и домино
Предположим, что у нас имеется шахматная доска
и 32 косточки домино, каждая величиной в две
клетки доски. Поставим на какую-нибудь клетку доски
пешку. Можно ли оставшуюся часть доски покрыть
костями домино так, чтобы ни одна кость не
вылезла за пределы доски и кости не налегали друг
на друга?
154. Две пешки и домино
Поставим две пешки на противоположные угловые
поля доски. Можно ли оставшуюся часть доски
покрыть костями домино так, как это требовалось в
предыдущей задаче?
155. Опять две пешки и домино
Поставим две пешки на поля разного цвета. Можно
ли оставшуюся часть доски покрыть костями домино?
156. Шахматные фигуры и домино
Сколько шахматных фигур нужно гюставить на
доску для того, чтобы на ней нельзя было разместить
ни одной кости домино?
157. О восьми королевах
На шахматной доске, состоящей из 64 клеток, расставить
восемь королев так, чтобы ни одна из них не
могла бить другую. Другими словами: на восьми
клетках шахматной доски поставить восемь королев
так, чтобы каждые две из них не были расположены
ни на одной линии, параллельной какому-либо краю,
86 ШАХМАТЫ в математике
и ни на одной из прямых, параллельных какой-нибудь
диагонали доски.
Этой задачей занимался знаменитый немецкий
математик Гаусс.
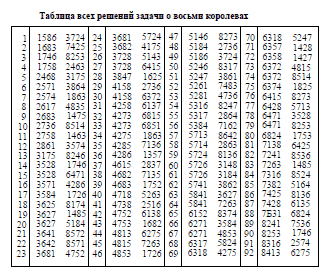
Покажем некоторые решения этой задачи и приведем
затем таблицу всех 92 ее решений.
На прилагаемом рис. 68 содержится одно из решений.
Обозначим это решение восемью цифрами
(6 8 2 4 1 7 5 3), где каждая цифра означает высоту
королевы в каждом столбце доски, т. е. 6 показывает,
что королева находится в первом столбце на шестой
клетке, считая снизу, 8 — что королева находится во
втором столбце на восьмой клетке, считая снизу,
и т. д. Мы и впредь вертикальные ряды клеток будем
называть столбцами, а горизонтальные — строками.
Строки мы тоже будем обозначать числами от 1
до 8 и считать их снизу вверх. Таким образом, записанное
нами выше с помощью одного ряда чисел первое
решение было бы правильнее записать так:
Если мы повернем доску на четверть окружности
в направлении, обратном движению часовой стрелки,
то из первого решения получим ему соответственное,
которое представлено у нас на рис. 69.
Чтобы получить это соответственное решение численно
из первого, достаточно расположить колонки
87 ШАХМАТЫ в математике
таблички (Л) так, чтобы цифры первой строки шли
в убывающем порядке:
8 7 6 5 4 3 2 1
‘ } 2 6 1 7 4 8 3 5
Цифры второй строки полученной таким способом
таблички образуют соответственное первому решение
( В ) : (2 6 1 7 4 8 3 5).
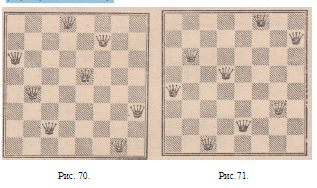
Следующие два рисунка (рис. 70, 71) представляют
второе и третье решения, соответственные рис. 68.
Их можно получить, заставляя шахматную доску
вращаться еще на четверть и еще на четверть окружности
в направлении, обратном движению часовой
стрелки. Можно вывести также, подобно предыдущему,
численное обозначение положения III
(рис. 70) из положения II (рис. 69), а положения IV
(рис. 71) из положения III. Но можно и прямо положение
III получить из I, а положение IV — из II.
Для этого поступаем так. Решения рис. 68 и 69
обозначены у нас рядами цифр:
(6 8 2 4 1 7 5 3) и (2 617 4 8 3 5).
Напишем эти цифры в обратном порядке:
(3 5 7 1 4 2 8 6) и (5 3 8 4 7 1 6 2),
и вычтем каждую из этих цифр из 9, получим
(6 4 2 8 5 7 1 3) и (4 6 1 5 2 8 3 7).
88 ШАХМАТЫ в математике
Это и будут численные обозначения решений на
рис. 70 и 71.
Таким образом, в общем случае некоторые решения
задачи о королевах дают место еще трем соответственным
решениям.
На рис. 72 дано другое решение задачи. Особенность
его заключается в том, что из него получается
только одно соответственное решение (рис. 73). В са-
мом деле, если повернуть шахматную доску на полуокружность,
то получаем опять то же расположение.
Ряд цифр (4 6 8 2 7 1 3 5), изображающий это решение,
отличается тем, что, сложенный с рядом, состоящим
из тех же цифр, но написанным е обратном порядке,
дает (9 9 9 9 9 9 9 9).
Возьмем какое-нибудь решение задачи о восьми
королевах и перевернем на рисунке порядок столбцов,
т. е. 1-й сделаем 8-м, 2-й сделаем 7-м и т. д. Или,
что сводится к тому же, напишем числовое обозначение
решения в обратном порядке — мы получим
решение, обратное данному. Легко убедиться, что это
решение отличается от всякого из соответственных
решений.
Опуская способы отыскания самых простейших
решений задачи, дадим эти решения на рис. 74. Каждое
из решений I—IX дает, как выше объяснено, 4 соответственных
и 4 обратных, т. е. всего 8 решений, последнее
же, XII, дает только 4 решения. Всего, следовательно,
получается 92 решения, которые исчерпывают
89 ШАХМАТЫ в математике
все решения задачи. Таблица всех этих решений приведена
на стр. 91.
Таблицу всех решений можно построить самому,
пользуясь следующим весьма простым систематическим
приемом. Помещают сначала одну королеву на
самую низкую клетку первого столбца слева, затем
ставят другую королеву во втором столбце опять на
90 ШАХМАТЫ в математике
самую низкую по возможности клетку и т. д., всегда
стремясь поместить в следующем столбце королеву
настолько низко, насколько это позволяют королевы,
стоящие слева. Когда наступит такой момент, что в
столбце нельзя поместить королеву, поднимают королеву
в предыдущем столбце на одну, две, три, …
клетки и продолжают размещать остальных королев,
руководствуясь всегда раз принятым правилом: поднимать
поставленных королев выше только в том случае,
если справа нет совсем места для следующей
королевы.
Всякий раз, когда решение найдено, его записывают,
и, таким образом, решения будут следовать одно
за другим тоже в последовательном числовом порядке.
Таблицу, полученную таким путем, можно проверять,
образуя соответственные и обратные решения,
которые можно вывести из первого и т. д.
158. О ходе шахматного коня
Мы встречались уже в этом разделе с BonpocoMs
может ли конь обойти часть шахматной доски, побывав
при этом на каждом поле только один раз.
91 ШАХМАТЫ в математике
Бот еще одна старинная задача о ходе шахматного
коня:
Представьте себе, что на какой-то из клеток шахматной
доски стоит конь. Требуется обойти этим конем
остальные 63 клетки, побывав на каждой из них только
один раз. На первый взгляд не ясно даже как подступиться
к этой задаче. Ведь для каждой из начальных
клеток должен быть свой путь. А может для некоторых
клеток такого пути вообще не существует. Задачей
этой занимался Эйлер и в письме к Гольдбаху
(26 апреля 1757 года) дал одно из решений ее. Вот
что, между прочим, пишет он в этом интересном
письме:
«…Воспоминание о предложенной когда-то мне задаче
послужило для меня недавно поводом к некоторым
тонким изысканиям, в которых обыкновенный
анализ, как кажется, не имеет никакого применения.
Вопрос состоит в следующем. Требуется обойти шахматным
конем все 64 клетки шахматной доски так,
чтобы на каждой клетке он побывал только один раз.
С этой целью все места, которые занимал конь при
своих последовательных ходах,
закрывались марками.
Но к этому присоединилось
еще требование, чтобы
начало хода делалось с данного
.места. Это последнее
условие казалось мне очень
затрудняющим вопрос. Я утверждаю,
однако, что если
полный обход коня будет
возвратный, т. е. если конь
из последнего места опять
может перейти на первое,
то устраняется и это затруднение.
После некоторых изысканий
по этому поводу я
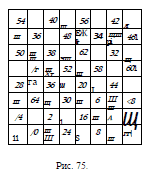
нашел, наконец, ясный способ
находить сколько угодно подобных решений (число
их, однако, не бесконечно), не делая проб. Подобное
решение представлено на рис. 75.
Конь ходит в порядке, указанном числами. Так
как из последнего места 64 он может перейти на 1* то
этот полный ход есть возвратный»*
92 ШАХМАТЫ в математике
Таково решение задачи о ходе шахматного коня,
данное Эйлером. В письме не указаны ни приемы, ни
путь, которыми знаменитый ученый пришел к своему
открытию. Сейчас мы укажем на методы иных, более
симметричных и методичных решений.
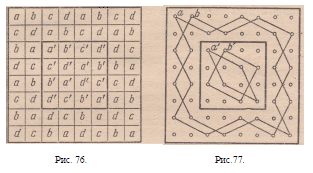
I. Разделим шахматную доску на две части: внутреннюю,
состоящую из 16 клеток, и краевую (рис. 76).
Каждые 12 клеток краевой части доски, обозначенные
у нас одинаковыми буквами, дают один из частных
зигзагообразных путей шахматного коня вокруг
доски; тачно так же четыре одноименные клетки
внутренней части доски дают частный замкнутый
путь шахматного коня в виде квадрата или в виде
ромба. Рис. 77 представляет два зигзагообразных частных
пути коня на краевой части доски. Эти пути
обозначены буквами а и Ь. Там же начерчены и два
пути на внутренней части доски. Эти пути назовем
а’ и Ъ’ соответственно обозначениям на рис. 76.
Закончив какой-нибудь частный круговой путь по
краевой части доски, конь может перескочить на любой
из трех путей другого наименования на внутренней
части доски. Нетрудно (стоит лишь взять в руки
шахматную доску и коня) найти, и притом различными
способами, четыре пути из 16 клеток — таких,
например, как
ab\ bc\ cd\ da’.
В самом деле, всмотритесь в рис. 76 и 77 или поставьте
перед собой шахматную доску, и вы увидите,
93 ШАХМАТЫ в математике
что для получения частного пути коня в 16 клеток
надо только краевой частный круговой путь из 12 кле-
ток соединить с внутренним путем, но другого наименования,
прямой чертой, уничтожая при этом в каждом
из частных круговых путей замыкающую линию
Так получим четыре частных круговых пути по 16 клеток.
Эти четыре частных пути по 16 клеток опять
можно соединить различным образом и получить
полный путь шахматного коня из 64 клеток.
Итак, ставят коня на какую-нибудь клетку, напри»
мер, краевой части доски и описывают по ней путь
из 12 клеток; вслед за тем конь перепрыгивает на
клетку одного из трех (не одноименных) внутренних
путей, проходит этот путь в любом направлении и перескакивает
опять на краевую часть, где снова делает
следующий частный зигзагообразный путь из 12 клеток,
вновь перескакивает на один из внутренних, не
одноименных с предыдущим, путей, описывает его,
переходит опять на новый краевой путь и т. д., пока
не обойдет все 64 клетки.
Способ решения задачи настолько прост и легок,
что не нуждается в более подробных разъяснениях и
указаниях.
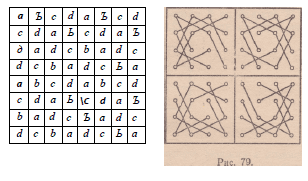
II. Можно эту же задачу решить и другим, не менее
легким, приемом. Здесь для удобства доска делится
на 4 части по 16 клеток в каждой двумя серединными
линиями (рис. 78). 16 клеток каждой четверти,
обозначенных одинаковыми буквами, можно
соединить посредством сторон двух квадратов и двух
ромбов, не имеющих ни одной общей вершины (рис. 79).
Соединяя, в свою очередь, одноименные квадраты и
ромбы всех четвертей доски, можно получить четыре
частных круговых возвратных пути из 16 клеток. Соединяя
затем эти последние пути, получим полный
путь коня в 64 клетки.
Полезно сделать еще следующие замечания. На
каждой четверти доски ромбами и квадратами обозначены
по четыре пути коня. Если соединим ромбы
и квадраты, обозначенные одинаковыми буквами во
всех четырех четвертях доски, получим по четыре
частных возвратных пути из 16 клеток.
Некоторые трудности могут представиться кому-
нибудь, когда для получения полного пути в 64 клетки
он начинает соединять между собой эти четыре
94 ШАХМАТЫ в математике
частных пути по 16 клеток. Здесь полезно иметь в
виду, что цепь (или ряд ходов) можно видоизменять%
не разрывая ее. Основдно это на следующем правиле.
Пусть имеем незамкнутую цепь ходов, проходящих
через клетки Л, В, С, Д Е} F, G, Я, /, /, К, Ь%
и пусть концы этой цепи будут А и L. Если клетка,
например D, отличная от предпоследней /С, находится
от последней L на расстоянии хода коня, то DE можно
заменить через DL и цепь ходов обратится в
A B C D L K J I H G F E ,
т. е. вторая половина цепи будет пройдена в обратном
порядке.
То же самое относится и к тому случаю, когда какая-
нибудь клетка, кроме второй, сообщается ходом
коня с первой. Итак, цепь (или ряд ходов) можно видоизменять,
не разрывая ее.
Число путей, которыми конь может обойти доску
и которые хможно найти указанными выше приемами,
не бесконечно. Но оно настолько огромно, что трудно
его представить.
95 ШАХМАТЫ в математике
Ё. И. ИГНАТЬЕВ В ЦАРСТВЕ СМЕКАЛКИ. Математика и шахматы. РЕШЕНИЯ, ОТВЕТЫ И ЗАМЕЧАНИЯ. XIII. ШАХМАТЫ.