ГЛАВА II ЯЗЫК АЛГЕБРЫ. Артель косцов.
ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман ИЗДАНИЕ ДВЕНАДЦАТОЕ СТЕРЕОТИПНОЕ
Под редакцией и с дополнениями В. Г. Болтянского
Скачать 11-ое издание ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман в формате PDF в хорошем качестве, но без возможности каптирования на Главной странице ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Текст для быстрого ознакомления (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):
Артель косцов
ЗАДАЧА
Известный физик А. В. Цингер в своих воспо-
минаниях о Л. Н. Толстом рассказывает о следую-
щей задаче, которая очень нравилась великому пи-
сателю:
«Артели косцов надо было скосить два луга, один
вдвое больше другого. Половину дня артель косила
большой луг. После этого артель разделилась попо-
лам: первая половина осталась на большом лугу и
стр. 39 Артель косцов.
докосила его к вечеру до конца; вторая же половина
косила малый луг, на котором к вечеру еще остался
участок, скошенный на другой день одним косцом за
один день работы.
Сколько косцов было в артели?».
РЕШЕНИЕ
В этом случае, кроме главного неизвестного — чис-
ла косцов, которое мы обозначим через х, — удобно
ввести еще и вспомогательное, именно — размер уча-
стка, скашиваемого одним косцом в 1 день; обозна-
чим его через f/. Хотя задача и не требует его опре*
деления, оно облегчит нам нахождение главного не-
известного.
Выразим через х и у площадь большого луга. Луг
этот косили полдня х косцов; они скосили
стр. 40 Артель косцов.
В артели было 8 косцов.
После напечатания первого издания «Заниматель-
ной алгебры» проф. А. В. Цингер прислал мне по-
дробное и весьма интересное сообщение, касающееся
этой задачи. Главный эффект задачи, по его мнению,
в том, что «она совсем не алгебраическая, а арифме-
тическая и притом крайне простая, затрудняющая
только своей нешаблонной формой».
«История этой задачи такова, — продолжает проф.
А. В. Цингер. — В Московском университете на мате-
матическом факультете в те времена, когда там учи-
лись мой отец и мой дядя И. И. Раевский (близкий
друг Л. Толстого), среди прочих предметов препо-
давалось нечто вроде педагогики. Для этой цели
студенты должны были посещать отведенную для уни-
верситета городскую народную школу и там в сотруд-
ничестве с опытными искусными учителями упраж-
няться в преподавании. Среди товарищей Цингера и
Раевского был некий студент Петров, по рассказам —
чрезвычайно одаренный и оригинальный человек. Этот
Петров (умерший очень молодым, кажется, от чахот-
ки) утверждал, что на уроках арифметики учеников
стр. 41 Артель косцов.
портят, приучая их к шаблонным задачам и к шаб-
лонным способам решения. Для подтверждения своей
мысли Петров изобретал задачи, которые вследствие
нешаблонности очень затрудняли «опытных искусных
учителей», но легко решались более способными уче-
никами, еще не испорченными учебой. К числу таких
задач (их Петров сочинил не-
сколько) относится и задача об
артели косцов. Опытные учителя,
разумеется, легко могли решать
ее при помощи уравнения, но
простое арифметическое решение
от них ускользало. Между тем,
задача настолько проста, что при-
влекать для ее решения алге-
браический аппарат совсем не
стоит.
Если большой луг полдня
косила вся артель и полдня
пол-артели, то ясно, что в
Толстой, всю жизнь любивший фокусные, не слиш-
ком хитрые задачи, эту задачу знал от моего отца
еще с молодых лет. Когда об этой задаче пришлось
беседовать мне с Толстым — уже стариком, его осо-
бенно восхитило то, что задача делается гораздо яс-
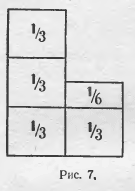
нее и прозрачнее, если при решении пользоваться са*
мым примитивным чертежом (рис. 7)».
Ниже нам встретятся еще несколько задач, кото-
рые при некоторой сообразительности проще реша-
ются арифметически, чем алгебраически.
стр. 42 Артель косцов.
На главную страницу ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Школьная математика. Математика в школе.


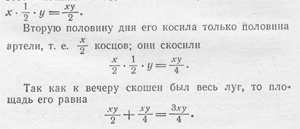




Comments