Составные числа.
| ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман ИЗДАНИЕ ДВЕНАДЦАТОЕ СТЕРЕОТИПНОЕПод редакцией и с дополнениями В. Г. Болтянского Сборник Математики На главную страницу ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман. Скачать 11-ое издание ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман в формате PDF в хорошем качестве, но без возможности каптирования на Главной странице ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман. |
Текст для быстрого ознакомления (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):
целых чисел, больших единицы, не делящихся без
остатка ни на какие другие целые числа, кроме еди-
ницы и самих себя, бесконечно велико.
Начинаясь числами 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, …, ряд их простирается без конца. Вклиниваясь
между числами составными, они разбивают нату-
ральный ряд чисел на более или менее длинные уча-
стки составных чисел. Какой длины бывают эти уча-
стки? Следует ли где-нибудь подряд, например,
тысяча составных чисел, не прерываясь ни одним
простым числом?
Можно доказать, — хотя это и может показаться
неправдоподобным, — что участки составных чисел
между простыми бывают любой длины. Нет гра-
ницы для длины таких участков: они могут состоять
из тысячи, из миллиона, из триллиона и т. д. состав-
ных чисел.
Для удобства будем пользоваться условным сим-
волом п\, который обозначает произведение всех чи*
сел от 1 до п включительно. Например 5! = 1 • 2 • 3 • 4 • 5.
Мы сейчас докажем, что ряд
стр. 92 Составные числа.
Числа эти идут непосредственно друг за другом в
натуральном ряду, так как каждое следующее на
1 больше предыдущего. Остается доказать, что все
они — составные.
Первое число
(n+1)! + 2=1x2x3x4x5x6x7… (n+1)+2.
•—четное, так как оба его слагаемых содержат
множитель 2. А всякое четное число, большее 2, — сос-
тавное.
Второе число
(n+1)! + 3=1x2x3x4x5x6x7… (n+1)+3.
состоит из двух слагаемых, каждое из которых крат-
но 3. Значит, и это число составное.
Третье число
(n+1)! + 4=1x2x3x4x5x6x7… (n+1)+4.
делится без остатка на 4, так как состоит из слагае-
мых, кратных 4.
Подобным же образом устанавливаем, что следую-
щее число
(n+1)! + 5
кратно 5 и т. д. Иначе говоря, каждое число на-
шего ряда содержит множитель, отличный от едини-
цы и его самого; оно является, следовательно, со-
ставным.
Если вы желаете написать, например, пять после-
довательных составных чисел, вам достаточно в при-
веденный выше ряд подставить вместо п число 5. Вы
получите ряд
722, 723, 724, 725, 726.
Но это — не единственный ряд из пяти последо-
вательных составных чисел. Имеются и другие, на-
пример,
62, 63, 64, 65, 66.
Или еще меньшие числа:
24, 25, 26, 27, 28.
стр. 93 Составные числа.
Попробуем теперь решить задачу:
Написать десять последовательных составных
чисел.
РЕШЕНИЕ
На основании ранее сказанного устанавливаем,
что в качестве первого из искомых десяти чисел мо-
жно взять
1x2x3x4-…x 10×11 + 2 = 39816802.
Искомой серией чисел, следовательно, может служить
такая:
39816 802, 39816 803, 39 816 804 и т. д.
Однако существуют серии из десяти гораздо меньших
последовательных составных чисел. Так, можно ука-
зать на серию даже не из десяти, а из тринадцати
составных последовательных чисел уже во второй
сотне!
114, 115, 116, 117 и т. д. до 126 включительно.
стр. 94 Составные числа.
На главную страницу ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Школьная математика. Математика в школе.

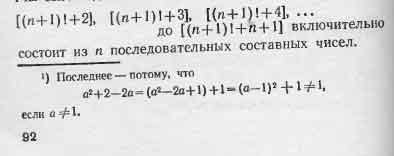


Comments