7. ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО).
Сборники Математики
Скачать бесплатно
Главная страница
КАБИНЕТ МАТЕМАТИКИ.
В. Г. БОЛТЯНСКИЙ, М. Б. ВОЛОВИЧ, Э. Ю. КРАСС, Г. Г. ЛЕВИТАС
ГЛАВА II. УЧЕБНОЕ ОБОРУДОВАНИЕ КАБИНЕТА МАТЕМАТИКИ.
Скачать книгу КАБИНЕТ МАТЕМАТИКИ в хорошем качестве (Сборник Математики №2).
Текст просто для быстрого ознакомления с темой в общих чертах (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):
Чрезвычайно полезны, хотя, к сожалению, и не получили
еще должного распространения в преподавании математики, материалы
с печатной основой, предназначенные для заполнения
учеником пробелов в текстах и чертежах. Тетради с печатной основой
(ТПО)—наиболее ценный из таких материалов.
1. В настоящее время, как и 5—6 лет назад, материалы с
печатной основой все еще являются новым видом учебного оборудования.
Существует необходимость перейти к массовому их
изготовлению. Разумеется, при этом следует критически осмыслить
тот опыт, который уже накоплен.
а) Например, в Латвийской ССР были недавно изданы тетради
по математике. В левой половине каждой страницы ‘этих
тетрадей напечатаны примеры. Правая половина каждой страницы
пустая. Например! (4а+36)3=….
Примеры расположены по одному на строке. Ученик, получив
на уроке такую тетрадь, накладывает на пустую половину
страницы чистый лист бумаги и против заданий пишет свои ответы.
Тем самым становится ненужным бессмысленное переписывание
условий. Ответы оказываются записанными в форме,
удобной для проверки. Одна и та же тетрадь может использоваться
многократно.
Однако это пособие имеет. ограниченное применение: оно
может содержать лишь такие задания, в которых нас интересует
только ответ. Между тем в тетради с печатной основой можно
включать и гораздо более разнообразные задачи.
б) Интересной модификацией материалов с печатной основой
являются перфорированные карточки, разработанные сотрудниками
НИИ педагогических наук Узбекской ССР. При работе
ученик скрепляет карточку с подложенным под нее листом
бумаги и вписывает недостающий текст в «окна». И здесь материалы
могут использоваться многократно, но характер заданий
становится более разнообразным.
Оба эти вида пособий роднит одно важное свойство: ответы
и тексты заданий находятся на разных листах, отозваны другот
друга, и для прочтения требуется их совмещать. Например, это
может оказаться неудобным при анализе в классе результатов
работы. И уж, конечно, работа, выполненная по этим заданиям,
не может быть использована в дальнейшем (скажем, для повторения
материала).
82 ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО). Материалы заданий.
Дополнительным недостатком перфорируемых карточек является
сложность их изготовления: каждая карточка перфорируется
по-своему, с. изменением формы и расположения
«окон».
2. Тетради с печатной основой отличаются от описанных
перфорированных карточек тем, что ученик, работая с ними, вписывает
свои ответы прямо в тетрадь, заполняет оставленные для
этой цели пробелы. Уже одно это делает использование ТПО
предпочтительным перед описанными видами пособий: ТПО
удобна для проверки и может быть использована учеником для
анализа и повторения материала, так как и задания, и ответы
ученика расположены слитно. Кроме того, ТПО может содержать
и принципиально иные задания, требующие изменения отпечатанного
в ней материала. Это задания такого же типа, как
при работе с контурными картами по географии, — задания на
достраивание чертежей, подчеркивание и зачеркивание, надписей,
раскраску и т. д. В описанных выше материалах такие задания
невозможны. Правда, это делает использование ТПО одноразовым,
что удорожает их. Однако эти затраты оправданны,
так как ТПО несравненно богаче по своим дидактическим возможностям
и изданных в Латвии тетрадей, и разработанных в
Узбекистане карточек. Вместе с тем необходимо отметить, что
ТПО просты в производстве и не отличаются в этом смысле от
обычной брошюры.
3. Среди включаемых в тетради с печатной основой задач
существенное место занимают такие, которые «избавляют учащихся
от неоправданного с педагогической точки зрения копирования
условий, чертежей и т. п.,
Именно такими задачами укомплектована тетрадь с печатной
основой, составленная К. С. Муравиным {82}: Вот характерное
задание этой тетради. На координатной сетке изображен
квадрат» Предлагается заштриховать ту область квадрата, в
которой находятся все точки, сумма координат каждой из которых
больше 9.
Здесь все вспомогательные,’ не существенные с точки зрения
данного задания построения сделаны заранее; ученик может, не
отвлекаясь, приступать к его выполнению. Работа с чертежом —
органическая часть решения, причем его копирование в тетрадь
из учебника было бы малоценной для данного случая операцией.
4. С помощью тетрадей с печатной основой могут быть даны
образцы деятельности.
а) В каждом из разработанных нашей лабораторией ком
плексов учебного оборудования тетрадям с печатной основой
принадлежит особо важная роль. В частности, задания, помещенные
в них, помогают учащимся усваивать новые понятия.
Приведем в качестве примера первые два задания тетради
с печатной основой по теме «Прямоугольный параллелепипед и
и его объем».
83 ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО). Материалы заданий.
Задание 1. Заполни пропуски в следующих
предложениях.
Чтобы узнать, является ли тело прямоугольным
параллелепипедом:
1) нужно сосчитать, сколько у него граней.
У прямоугольного парраллелепипеда;_________
граней;
2) нужно посмотреть, являются ли все
Рис. 15 грани тела прямоугольниками. У прямоугольного
параллелепипеда все грани •
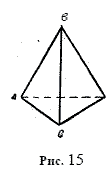
Задание 2. Определи, является ли это тело прямоугольным
параллелепипедом (рис. 15).
Решение. Сосчитаем, сколько граней у этого тела. У этого
тела граней. У прямоугольного параллелепипеда
__________ граней.
Ответ. Это тело не является _________________ .
Хотелось бы обратить внимание читателя на следующие особенности
приведенных заданий.
В них пропущено сравнительно немного слов: мы стремились
максимально освободить учащегося от непроизводительного
для урока математики труда. Конечно, пропущены не случайные
слова, а такие, которые заставят ученика лишний раз
обратиться к определениям, задуматься над последовательностью
операцйй и т. д.
Задачи представляют образцы и оформления, и рассуждений
и одновременно требуют выполнения строго определенной
деятельности. При этом учащиеся вынуждены работать с определением,
которое в рассматриваемой тетради приводилось здесь
же, перед заданиями. В ходе выполнения этих (и других) заданий
определение запоминалось. Как показал эксперимент, никакого
предварительного заучивания не потребовалось.
Итак, в тетрадь с печатной оснбвой полезно включать разъяснение
того, каким образом и в какой последовательности
должны выполняться операции, в ходе которых усваиваются
знания. Это разъяснение часто содержится в целых циклах заданий.
Например, при изучении темы «Прямоугольный параллелепипед
и его объем» учащиеся должны получить представление
об объеме как о числе, показывающем, сколько единиц объема
содержится в данном теле.
Деятельность, необходимая для усвоения понятия «объем
прямоугольного параллелепипеда», заключается в подсчете единичных
кубов, на которые может быть «разрезано» данное тело.
В ходе этой деятельности должен быть открыт удобный способ
подсчета: формула для вычисления объема прямоугольного параллелепипеда.
84 ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО). Материалы заданий.
В комплексе учебного оборудования по этой теме деятель-
лость по пересчету единичных кубов осуществляется при помощи
разных предметов учебного оборудования, в том числе и при помощи
заданий 32—34 тетради с печатной основой, которые мы
приводим.
Задание 32. Определи объем тела (рис. 16).
Решение. Чтобы узнать объем тела, нужно сосчитать, сколько
в этом теле содержится В этом теле содержится 4
единиц объема. Значит, объем его равен_______________ ______ .
Ответ. Объем тела равен .
Задание 33. У этого куба одно из ребер увеличили в три
раза, а остальные измерения не меняли. Нарисуй получившийся
прямоугольный параллелепипед (рис. 17).
Считая куб единичным, определи объем прямоугольного
параллелепипеда.
Решение. Чтобы узнать объем прямоугольного параллелепипеда,
нужно подсчитать__________5 Ответ. Объем тела равен ________ ,
Задание 34. У этого куба два измерения увеличили в два
раза, а третье измерение не меняли. Нарисуй получившийся прямоугольный
параллелепипед (рис. 18).
Считая куб единичным, определи объем прямоугольного
параллелепипеда.
Ответ. Объем прямоугольного параллелепипеда равен .
Однако пересчет по одному единичных кубов, из которых
сложено тело, — нерациональный способ определения объема.
Нужны средства’обучения, которые позволили бы разъяснить
идею опосредованного подсчета числа единичных кубов, составляющих
прямоугольный параллелепипед. Эта задача также решается
при помощи различных предметов учебного оборудования,
и в частности заданий 35—37 тетради с печатной основой.
Задание 35. Найти объем этого прямоугольного параллелепипеда
(в кубических сантиметрах) (рис. 19).
Решение. Объем одного слоя равен куб. см. Всего ело-*
ев ____ . Объем прямоугольного параллелепипеда равен_________
куб. см.
Ответ _________ .
85 ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО). Материалы заданий.
Задание 36. Длина прямоугольника 5 см, ширина 2 см.
Сколько кубиков с ребром в 1 см можно разместить на этом прямоугольнике
в один слой? в четыре слоя? Нарисуй получившиеся
при этом прямоугольные параллелепипеды и определи их
объемы (рис. 20).
Решение. В один слой на прямоугольнике можно разместить
кубиков. В четыре слоя на прямоугольнике можно разместить
_____ кубиков-.
Ответ. Объем прямоугольного параллелепипеда, составленного
из кубиков в четыре слоя, равен_________ куб. см,
Задание 37. Каждое измерение куба уменьшили в три раза
(рис. 21).
1) Нарисуй получившийся куб.
. 2) Разбей нижнее основание на такие квадраты, чтобы на
каждой квадрат можно было положить малый куб.
3) Сколько малых кубов можно уместить на нижнем основании
большого куба?
На нижием основании большого куба можно уместить _____
малых кубов.
4) Сколько малых кубов можно уместить на передней грани
большого куба? —
На передней грани большого куба можно уместить
малых кубов. ■
5) Считая малый куб единичным, определи объем большого
куба.
Ответ. Объем большого куба равен „
Учащимся легко подсчитать число единичных кубов, составляющих
данный прямоугольный параллелепипед, в том случае,
когда он разделен на кубы. Учителю нетрудно объяснить и то, что
объем прямоугольного параллелепипеда получается перемножением
его измерений или умножением площади основания
на высоту. Однако если этим ограничиться и сразу перейти к вы—
числению объемов с помощью формул, причем тренировать учащихся
лишь в перемножении чисел, то они очень скоро забудут
все наши рассуждения: в их сознании подсчет кубов не будет связан
с вычислением объемов по формулам. Но комплекс [7] предусматривает
постепенное «снятие материализации». Например,
некоторое время учащиеся должны определять объем прямо-
86 ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО). Материалы заданий.
угольного параллелепипеда, у которого указаны измерения, рассказывая
и показывая, каким образом подсчитывать единичные
кубы. Даже после того, как учащиеся успешно вычислили несколько
раз объем по формулам, полезно возвратиться (и не один
раз) к подсчету единичных кубов. Для этой цели могут быть использованы,
в частности, задания, аналогичные заданию 40 тетради
с печатной основой.
Задание 40, Измерения прямоугольного параллелепипеда
равны 6, 3 и 2 единицам длины (рис. 22).
1) Определи объем этого прямоугольного параллелепипеда.
Объем прямоугольного ^параллелепипеда ‘равен»
Получившееся число показывает _______________________ _.
2) Начерти единицу объема, с помощью которой измерен
объем данного прямоугольного параллелепипеда.
б) Тетрадь с печатной основой дает возможность отрабатывать
понятия и прививать учащимся навыки решения типовых
задач. Она же может подсказать пути решения нестандартных
задач.-Вот, например, два задания из той же тетради.
Задание 14. Сколько сантиметров проволоки пошло на изготовление
каркаса этого прямоугольного параллелепипеда
(рис. 23)? Реши задачу двумя способами.
Первый способ:
1) На ребра нижнего основания пошло см.
2) На ребра верхнего основания пошло ___ см.
3) На вертикальные ребра пошло см.
,4) Всего на каркас пошло _____ см.
Второй способ: —
1) На три неравных ребра пошло. ____ см.
‘ 2) Всего на каркас пошло см.
Задание 44. Объемпервого куба равен сумме объемов трех
остальных (рис. 24). Чему равно ребро первого куба?
Решение. По таблице кубов (смотри обложку1) находим,
что:
Объем куба с ребром 3 равен
1 На обложке напечатана таблица кубов чисел первой сотни.
87 ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО). Материалы заданий.
Объем куба с реб,ром 4 равен _____ г
Объем куба с ребром 5 равен _____ *
Значит, сумма объемов всех трех кубов {равна 27+’________ +
4- — • а это и есть объем первого куба.
По таблице кубов находим, что его ребро ‘равно
Ответ. Ребро первого куба равно
5. Использование материалов с печатной основой приводит
к большой экономии времени ученика и учителя, позволяет учителю
осуществить индивидуальный подход на каждом уроке, вовремя
помочь отстающим ученикам, «догрузить» сильных дополнительными
заданиями.
Приведем задание, которое может быть использовано с указанными
выше целями, из той же ТПО по теме «Объем прямоугольного
параллелепипеда».
Задание 28. По данным таблицы вычисли площадь пола
каждой комнаты, а затем объем каждой комнаты. Подсчитай
общий объем всех трех комнат
Тетрадь с печатной основой успешно используется и тогда,
когда формулировка задачи, связанная, например, с чертежом,
отнимает непропорционально много труда и времени по сравнению
с процессом решения. Вот пример.
Задание 7. Дорисуй изображение куба (рис. 25),
88 ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО). Материалы заданий.
Задание 8. Обведи ребра изображенного
здесь прямоугольного параллелепипеда,
чтобы они оказались окрашенными в !
один цвет (рис. 26).
6. Важной особенностью тетради с печатной
основой является ее ярко выраженная
дидактическая направленность. С хорошо
составленной тетрадью ученик может
работать дома. Нам известны случаи, когда
ученики IV класса совершенно самостоятельно выполнили все
задания тетради «Объем прямоугольного параллелепипеда».
Подбирая правильную последовательность заданий и освобождая
ученика от выписывания части текста решения (предлагая
этот текст в готовом виде), мы тем самым даем ему направление
в решении задачи. Такое руководство необходимо при первоначальном
обучении новым понятиям и операциям.
89 ТЕТРАДИ С ПЕЧАТНОЙ ОСНОВОЙ (ТПО). Материалы заданий.



Comments