ПРЯМАЯ ЛИНИЯ. ГЛАВА 1. УГЛЫ.

ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

 

ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

ПРЯМАЯ ЛИНИЯ УГЛЫ

Скачать всю книгу Ж. АДАМАР «ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ» в хорошем качестве
Ниже посмотрите текст для быстрого ознакомления(формулы отображаются не корректно):

10. Углом называется фигура, образованная двумя полупрямыми,
выходящими из одной и той же точки. Эта точка называется вершиной
угла, а две полупрямые — его сторонами.
Угол обозначается той же буквой, что и его вершина, помещённой
между двумя другими буквами, которые служат для обозначения
его сторон; перед буквами часто ставится специальный знак.
Если, впрочем, фигура содержит только один
угол, имеющий данную вершину, то буква,
обозначающая эту вершину, будет вполне достаточна
для обозначения угла. Так, угол, образованный
полупрямыми АВ, АС , будет
обозначаться: 2. ВАС, или проще А.
Два угла называются равными по определе-
А 8 нию равных фигур (п. 3), если их можно приве-
Черт. 8. сти в совпадение, накладывая один на другой.
Два равных угла ВАС и ВГАГСГ могут быть наложены один
на другой двумя различными способами, а именно: или так, что
сторона АГВТ совпадает со стороной АВ и А!С со стороной ЛС,
или наоборот. От одного способа совмещения можно перейти к другому,
перевёртывая один из углов и накладывая
его на самого себя, например, перемещая
угол ВАС так, чтобы сторона АВ приняла положение,
ранее занимаемое ЛС, и обратно.
11. Два угла называются прилежащими
друг к другу, если они имеют общую вершину,
одну общую сторону и расположены по разные
стороны от этой общей стороны.
Если два угла £АОВ и ВОС—приле-
жащие (черт. 9), то угол АОС называется суммою
этих двух углов. Сумма нескольких углов не зависит от порядка
слагаемых.
Чтобы сравнить два угла, их перемещают таким образом, чтобы
они имели общую вершину, одну общую сторону и чтобы они были
расположены по одну сторону от их общей стороны.
Пусть даны два угла АОВ и £ ЛОС, расположенные таким
образом, Если при вращении вокруг точки О мы встретим стороны

26 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

в порядке ОЛ, ОВ, ОС (черт. 9), то угол АОС равен сумме углов
АОВ и ВОС\ в этом случае говорят, что он больше угла АОВ, а
этот последний меньше угла АОС; если, напротив (черт. 10),

порядок таков: О А, ОС, ОВ, то угол АОВ больше угла АОС. Угол БОС,
от прибавления которого к одному из двух данных углов получается
другой угол, есть разность этих двух углов.
Наконец, в случае промежуточном, когда ОВ совпадает с ОС,
оба угла равны (см. предыдущий пункт).
Внутри всякого угла ВАС существует полупрямая AM, которая
делит этот угол на две равные части. Она называется биссектрисой
угла. Полупрямые, выходящие из Л и расположенные
внутри угла ВАМ, образуют с АВ угол
меньший, чем с ЛС; обратное имеет место для
полупрямых, расположенных внутри угла MAC.
Некоторый угол тзывгетсяу двоенным,у троенным
и т. д. углом по отношению к данному углу,
если он представляет собой сумму двух, трёх Черт.10.
и т. д. углов, равных этому углу. Этот последний
называется при этом половиной, третью и т. д. первого.
П р и м е ч а н и е . Очевидно, величина угла не зависит от величины
его сторон, которые мы должны всегда предполагать неограниченно
продолженными.
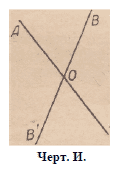
12. Если мы имеем угол, образованный двумя
полупрямыми О А и ОВ (черт. 11),

и если продолжить
О А за точку О, проведя О Л’, и то же самое
сделать с ОВ, проведя ОВТ, то образуется новый
угол А’ОВ\
Вертикальными углами называются два угла,
АОВ, А’ОВ\ таких, что стороны одного
являются продолжениями сторон другого.
Черт. И. Теорема. Два вертикальных угла равны
между собой.
В самом деле, перевернём угол ВОАг и наложим его на самого
себя (черт. 11). Сторона ОВ займёт положение ОЛ’, и, с другой
стороны, сторона ОАг займёт первоначальное положение стороны ОВ;
полупрямая ОЛ, как продолжение ОЛ’, пойдёт по ОВ\ как по продолжению
ОВ. Угол АОВ займёт тогда положение угла АгОВг,
следовательно, эти два угла равны.
13. Всякая полупрямая, выходящая из центра окружности, пересекает
эту окружность в одной и только в одной точке.
Всякий угол АОВ (черт. 5), имеющий вершину в центре О
окружности (центральный угол), определяет на этой последней
дугу АВ, ограниченную точками пересечения окружности со сторонами
угла. Эта дуга во всяком случае меньше, чем полуокружность,
как в этом можно убедиться, принимая за концы полуокружности
точку Л и точку, ей диаметрально противоположную.
Обратно, зсякую дугу, меньшую полуокружности, можно, рас-

27 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

сматривать как отсекаемую центральным углом; этот угол образован
радиусами, проведёнными в концы данной дуги.
Теорема. На одной и той же окружности или на равных
окружное тях:
1°. равным дугам (меньшим полуокружности) соответствуют
равные центральные углы, и обратно;
2°. неравным дугам (меньшим полуокружности) соответствуют
неравные центральные углы, и большей дуге соответствует больший
центральный угол\
3°. если некоторая дуга(меньшая полуокружности) есть сумма
двух других дуг, то и соответствующий ей центральный угол будет
суммой центральных углов, соответствующих двум другим дугам.
1°, 2°. Пусть АВ, АС (черт. 5) — две дуги одной и той же окружности,
выходящие из одной точки А в одном и том же направлении
(п. 8). Два центральных угла АОВ, АОС будут при этом расположены
так, как это было сказано в п. 11. Полупрямые О А, О В,
ОС следуют в том же порядке, как точки Л, В, С на окружности.
Кроме того, если прямые ОВ и ОС совпадают, то это же имеет
место для точек В и С, и обратно.
3°. Так как для построения суммы двух дуг (п. 8а) эти дуги располагают
так, как расположены дуги АВ, БС(черт. 5), то центральный угол
АОС, соответствующий сумме дуг, будет суммой двух центральных углов
£ АОВ и ВОС, которые будут прилежащими друг к другу.
На этом основании, чтобы сравнить различные углы, можно из
их вершин, как из центров, описать окружности одним и тем же
раз навсегда выбранным радиусом и сравнить дуги, отсекаемые на
этих окружностях.
Деление угла на две или больше равные между собой части
сводитсяк делению на равные части дуги, отсекаемой сторонами
угла на окружности, имеющей центр в вершине
угла.
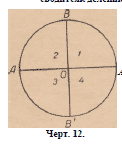
14. Говорят, что две прямые взаимно
перпендикулярны, если из четырёх углов,
которые они образуют, два угла, прилежа-
А щих друг к другу, равны между собой. Например,
прямая ЛОЛ’ (черт. 12)

перпендикулярна
к прямой ВОВ’, если углы, обозначенные
на чертеже номерами 1 и 2, между
собой равны. В этом случае все четы-
Черт. 12. ре угла при точке О будут между собой
равны, потому что £ 3 и £4
(черт. 12) соответственно равны 1 и А2 как вертикальные.
Угол, стороны которого перпендикулярны между собой, называется
прямым.
Теорема. В данной плоскости через точку, взятую на прямой,
можно провести к этой прямой перпендикуляр и притом

28 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

Пусть через точку О требуется провести перпендикуляр к данной
прямой, проходящей через эту точку. Достаточно провести из.точки О,
как из центра, окружность, которая пересечёт данную прямую в точках
А и А’ (черт. 12), и разделить на две равные части точкой В
полуокружность АВА’. ОВ будет искомым перпендикуляром; и обратно,
перпендикуляр к АА’, проходящий через точку О, должен делить
на две равные части полуокружность АВА’.
Следствие. Мы видим, что прямой угол отсекает
на окружности, имеющей центр в вершине
угла, дугу, равную четверти этой окружности.
Все прямые углы равны между собой, так как
на равных окружностях, имеющих центры в вершине
каждого из них, они отсекают равные дуги.
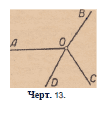
15. Если через одну точку провести Черт. 13.

несколько полупрямых, то сумма всех последовательных
углов (Z. АОВ, ВОС, COD, DO А, черт. 13), образованных
таким образом около этой точки, равна четырём прямым.
Действительно, сумма дуг, отсекаемых этими углами на окружности,
имеющей своим центром данную точку, равна полной окружности.
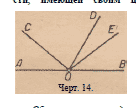
Если через точку, лежащую на прямой,
провести по одну сторону от этой прямой
несколько полупрямых (черт. 14), то сумма
образованных таким образом углов
равна двум прямым, так как сумма дуг,
отсекаемых этими углами, равна полуокружности.
или несколько углов при одной и той же
каждый является прилежащим к предыду-
Черт. 14.

Обратно если два
вершине, из которых
щему (А АОС, Л COD, £DOE, /ЕОВ,
черт. 14), составляют в сумме два прямых, то
крайние стороны этих углов лежат на одной
прямой линии.
В самом деле, эти крайние стороны пересекают
окружность, имеющую центр в общей
вершине углов, в двух диаметрально противоположных
точках, так как дуга, заключённая
между ними, составляет полуокружность.
15а. Теорема. Биссектрисы четырёх углов,
образованных двумя пересекающимися
прямыми, образуют две бесконечные прямые,
перпендикулярные между собой.

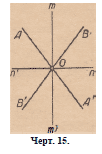
Черт. 15.

Пусть АА’ и ВБ’ (черт. 15)а—две прямые, которые пересекаются
в точке О и образуют углы АОВ, БОА’, А’ОБ’, В О А, биссектрисами
которых служат От, On, От!, On’; я утверждаю;
1) что От и От’являются продолжениями одна другой, так же
как Ол и Оп’\

29 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж.

2) что полученные таким образом две прямые взаимно перпендикулярны.
Прежде всего От перпендикулярна к On, так как два угла АОВ
и ВО А! в сумме составляют два прямых, а потому их половины——————-
тОВ и ВОп,— дают в сумме один прямой. Но, применяя то же
самое рассуждение к углам ВОАг и А’ОВ\ мы видим, что прямая От!
перпендикулярна к On. Следовательно, От! является продолжением
От\ и точно так же Опг есть продолжение On.
16. Острым углом называется угол, меньший прямого; тупым —
угол, больший прямого.
Два угла называются дополнительными, если их сумма равна
прямому углу, и пополнительными, если их сумма равна двум
прямым.
17. Отношением двух величин одного и того же рода называется
число, которое показывает, сколько раз одна величина содержит
другую величину или какую-либо р-ую часть другой величины
(р — целое), и какую именно.
Например, если, разделив отрезок АВ на 5 равных частей, мы
увидим, что одна из этих частей ровно три раза содержится в отрезке
ВС, то мы скажем, что отношение ВС к АВ равно
Если же, напротив, пятая часть отрезка АВ не содержится целое
число раз в отрезке ВС, например, если она в этом отрезке содер-
3
жится больше чем 3 раза и меньше чем 4 раза, то будет прибли-
женным значением отношения , ВСп *р ичём это бу*дет значение, взятое
с точностью до -g- по недостатку (значение с точностью до
у, взятое по избытку, будет —).
Отношение этих двух величин а и b одного рода равно отношению
двух других величин а\ ЬТ одного рода (но не обязательно
того же рода, как первые), если, каково бы ни было я, значение
первого отношения, взятое с точностью до —, равно значен1ию
1 второго отношения, взятому с точностью до —.
Мера данной величины по отношению к определённой величине
такого же рода, принятой за единицу, есть отношение данной
величины к этой единице.
Можно доказать следующие свойства:
1°. Дее величины, имеющие одну и ту же меру по отношению
к одной и той же единице, равны.
2°. Отношение двух величин одного и того же рода равно
отношению чисел, служащих их мерой по отношению к одной
и той же единице,

30 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

3°. Отношение двух чисел равно частному этих двух чисел.
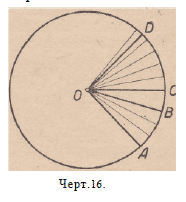
Теорема. В одной окружности или равных окружностях
отношение двух центральных углов равно отношению двух дуг,
которые заключены между их сторонами.
Пусть1) даны (черт. 16) две дуги АВ и CD окружности О. Разделим
центральный угол АОВ, например, на три равные части и
предположим, что одна из этих частей содержится в угле COD
больше чем 4 раза, но меньше чем 5 раз; тогда с точностью до
величина отношения ■ L COD есть 4 L. AUn о
Но, деля угол АОВ на три равные части, мы в то же время
разделили дугу АВ на три равные части (п. 13). Если бы треть
угла АОВ могла уложиться 4 раза, но не
5 раз в угле COD, то это показывало бы,
что треть дуги АВ могла бы уложиться
в дуге CD 4 раза, но не 5 раз.
Значения двух отношений, измеренные
с точностью до 1у, равны; совершенно так
же равны между собой значения двух отношений,
взятые с точностью до для
любого значения п\ теорема, таким образом,
доказана. Черт. 16.

Следствие. Если принять за единицу
угла центральный угол, который заключает между сторонами
дугу, принятую за единицу, то всякий центральный угол имеет
ту же меру, как и дуга, заключённая между его сторонами.
Это предложение сводится к предыдущему, так как мера величины
есть отношение этой величины к своей единице.
Предполагая, как мы это будем делать в последующем, что на
каждой окружности за единицу дуг принимается дуга, заключённая
между сторонами центрального угла, принятого за единицу
углов, можно предыдущее следствие сформулировать так: центральный
угол измеряется дугой, заключённой между его сторонами.
18. Только что установленные определения позволяют нам ввести
одно важное соглашение.
*) Теорема становится очевидной, если Допустить следующее арифметическое
предложение (Т а н н е р и, Курс арифметики, гл. XIII, п° 493): Две
величины пропорциональны, если: 1) одному и тому же значению первой
соответствует всегда одно и то же значение второй и 2) сумме двух
значений первой величины соответствует сумма двух соответствующих
значений второй величины. Эти два условия здесь выполнены (п. 13).
Доказательство в тексте лишь воспроизводит для данного частного слуА
чая доказательство общей арифметической теоремы.

31 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

Прежде всего мы можем предположить, что все величины, о которых
мы будем говорить, измерены определённо выбранной единицей,
для каждого рода величин; далее, что во всех равенствах, которые
мы будем писать, количества, входящие в ту и другую часть равенства,
представляют собой не самые величины, а лишь меры этих величин.
Таким образом, мы можем написать целый ряд равенств, которые
без этих предположений не имели бы никакого смысла. Например,
можно приравнять друг другу две разнородные величины, если имеется
равенство двух чисел, которые их измеряют; смысл равенства в
этом случае совершенно ясен. Мы сможем точно так же писать
произведение двух каких-либо величин, так как произведение двух
чисел уже определено, и т. д.
Впрочем, когда мы будем писать, как до сих пор, равенство
двух величин одного и того же рода, — это равенство будет иметь
точно такой же смысл, как и раньше, так как равенство двух
величин и равенство их мер сводится одно к другому (п. 17).
На основании этого соглашения возможно написать, если АВ —
некоторая дуга и О — центр окружности:
АОВ ~ дуге АВ.
Во всяком случае очень важно подчеркнуть, что это равенство
существенно предполагает, что единица угла и единица дуги выбраны
так, что указанное выше условие удовлетворено.
18а. Окружность обычно делится на 360 равных частей, называемых
градусами, каждый из которых содержит 60 минут; каждая
минута в свою очередь делится на 60 секунд. При этом дуги
измеряются в градусах, а следовательно, и углы тоже измеряются
в градусах. Число градусов, минут и секунд, заключающееся в угле,
равно числу градусов, минут и секунд дуги, отсекаемой этим углом
на окружности, имеющей центр в вершине угла; прямой угол соответствует
четверти окружности, или 90 градусам. Отсюда следует,
что мера центрального угла не зависит от радиуса окружности, на
которой отсчитываются дуги, так как выбранная угловая единица
(градус) по величине не зависит от этого радиуса, а именно составляет
одну девяностую часть прямого угла.
Для записи величины углов (или дуг) в градусах, минутах и
секундах пользуются следующими обозначениями: угол в 87 градусов,
34 минуты и 25 секунд записывается так: 87°34’25».
Введение десятичной системы во всех других видах измерений
приводит к установлению другого способа подразделения окруж-‘
ности, при котором она делится не на 360, а на 400 равных частей,
называемых градами. Град, очевидно, несколько меньше градуса
и составляет сотую часть прямого угла.
Град подразделяется также по принципу десятичной системы: строго
говоря, нет необходимости давать этим подразделениям специальные
названия, они пишутся просто по принципу десятичной нумерации.

32 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

Таким образом, можно говорить об угле 3°,5417 (т. е. 3 града
и 5417 десятитысячных).
Однако сотую часть града часто называют десятичной минутой
и обозначают её значком ‘ (вместо значка ‘, обозначающего шестидесятеричную
минуту, т. е. шестидесятую долю градуса); точно так же
сотая часть десятичной минуты (десятитысячная часть града) представляет
собой десятичную секунду, обозначаемую знаком». Таким образом,
предыдущий угол по этой системе может быть написан так:
3°64Ч7\
Один град составляет -щ-, ил3и6 0° 9 а градуса, или 54’. Один градус
составляет 1° 11′, 1 . . . (или иначе ~ града).
19. Теорема. Через точку, взятую вне прямой, можно провести
перпендикуляр к этой прямой и притом только один.
1°. Возможно провести перпендикуляр. Пусть даны точка О и
прямая ХУ (черт. 17). Повернём полуплоскость, содержащую точку О,
около прямой ХУ, как около оси, так, q
чтобы она совместилась с другой полуплоскостью.
Точка О попадёт в &.
Соединим их прямой ООг.
Эта прямая пересечёт ХУ, так как
она соединяет две точки, расположенные
по разные стороны от прямой ХУ.
Пусть I— точка пересечения. Углы 04 X
и О1Х—прямые, так как угол ОЧХ
представляет собой то положение,
которое принимает угол OIX, когда
одну из полуплоскостей совмещают с Черт. 17.

другой путём вращения около ХУ.
Следовательно, две прямые ХУ и 00Т перпендикулярны.
2°. Можно провести только один перпендикуляр. Пусть ОМ —
какой-либо перпендикуляр к ХУ, проведённый через точку О; продолжим
эту прямую на длину МО», равную ОМ. Если мы совместим
снова одну из полуплоскостей с другой, прямая МО пойдёт по МО»,
так как углы О MX и О” MX равны как прямые, а так как МО” = МО,
то точка О попадёт в точку О»; следовательно, точка О» совпадёт
с точкой О’, и прямая 00″ совпадёт с ООг.
19а. Точка называется симметричной с данной точкой О относительно
прямой ХУ, если она лежит на продолжении перпендикуляра,
проведённого к прямой ХУ через точку О, на расстоянии, равном
длине этого перпендикуляра. Из предыдущего следует, что точка,
;имметричная с точкой О, представляет собой то положение, кото-
оое занимает точка О после поворота (п. 19, 1°) около оси ХУ.
ссли дана какая-нибудь фигура, можно построить симметричные

33 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

точки для каждой точки этой фигуры. Совокупность симметричных
точек образует новую фигуру, которая называется симметричной
с первой фигурой. Отсюда видно, что для получения фигуры,
симметричной с данной фигурой относительно прямой ХУ, можно
повернуть плоскость, в которой лежит фигура, вокруг ХУ так, чтобы
каждая полуплоскость, определяемая этой прямой, совместилась
с другой полуплоскостью, и отметить новое положение, занятое
данной фигурой. Отсюда следует:
Теорема. Две симметричные плоские фигуры равны.
Следствие. Фигура, симметричная прямой линии, — прямая
линия.
Если какая-либо фигура совпадает со своей симметричной относительно
прямой ХУу то говорят, что она симметрична относительно
этой прямой, или, иначе, что она имеет эту прямую осью симметрии.
20. Чтобы совместить фигуру F с фигурой F, ей симметричной,
мы должны выполнить такое движение, при котором фигура выйдет
из своей плоскости. Следует заметить, что *)
невозможно достигнуть совмещения без
такого движения; это происходит оттого,
что направление вращения обратно в обеих
фигурах. Объясним, что следует понимать
под этим выражением.
церТ Прежде всего заметим, что плоскость
фигуры делит пространство на две области.
Назовём одну из этих областей для краткости областью, расположенной
над плоскостью, другую — под плоскостью.
Допустим, что на фигуре F имеем угол ВАС, который можно
рассматривать как образованный полупрямой, перемещающейся внутри
угла из положения АВ в положение АС (черт. 18). При взгляде на
плоскость сверху мы будем говорить об этом угле, что он имеет
отрицательное или положительное направление, смотря по тому,
представляется ли вращение этой полупрямой происходящим по
часовой стрелке или в обратном направлении2).

Положим для определённости, что имеет место последний случай.
Тогда наблюдатель, лежащий на АВ ногами в сторону Л, а головой
по направлению к В и смотрящий под плоскость, увидит сторону АС
слева от себя; следовательно, если, оставаясь расположенным вдоль
по АВ, он посмотрит на сторону ЛС, то окажется, что часть пространства,
находящуюся под плоскостью, он увидит справа от себя.
Ясно, что при взгляде на плоскость снизу можно повторить всё
вышеизложенное, заменяя слово „над» словом „под» и обратно. Так
как наблюдатель, расположенный вдоль по АВ и смотрящий на ЛС,
J) В общем случае. Прим. ред. перевода.
2) Заметим, что для того, чтобы указать направление вращения, следует
принимать во внимание порядок, в котором рассматриваются стороны угла.
Так, угол ВАС имеет противоположное направление по отношению к
углу сАв

34 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

будет необходимо иметь верх плоскости слева, если низ плоскости
находится от него справа, и обратно, то направление вращения
меняется в зависимости от того, смотрим ли мы на плоскость
с одной или с другой стороны плоскости1).
Предположим теперь, что некоторый угол произвольно перемещается
в своей плоскости, не выходя из неё. Наблюдатель, участвующий
в этом движении, не изменит своего положения по отношению
к верху и низу плоскости, так что направление вращения остаётся
неизменным при всяком перемещении, не выводящем фигуры из её
плоскости.
Чтобы показать, что такое движение не может совместить фигуру F
с симметричной ей фигурой F\ достаточно поэтому показать, что
направление вращения противоположно в обеих фигурах. Действительно,
мы видели, что переход от F к Fr можно осуществить вращением
плоскости около оси ХУ так, чтобы она совпала сама с собой
(п. 19а). При этом повороте точки, расположенные над плоскостью,
оказываются под плоскостью, и обратно. Направление какого-либо
угла фигуры F при взгляде снизу будет то же, что и направление
угла с ним симметричного при взгляде сверху. Таким образом, при
взгляде с одной и той же стороны направление углов будет противоположным.
20а. П р и м е ч а н и я : I. Ясно, что, точно так же как и угол, дуга
может иметь направление положительное или отрицательное, что зависит/
конечно, от порядка, в котором мы рассматриваем концы дуги.
И. Иногда говорят, что плоскость ориентирована, если на ней
указано положительное направление углов. На основании предыдущего
ориентировать плоскость — значит указать, которую из двух областей
пространства мы будем называть расположенной над плоскостью.

УПРАЖНЕНИЯ.

1. Если точка М — середина отрезка АВ, то расстояние СМ равно
полуразности отрезков СЛ и СВ, если точка С лежит на самом отрезке,
и полусумме С А и СВ, если точка С взята на продолжении АВ (доказать).
2. Если ОМ — биссектриса угла АОВ, то угол СОМ равен полуразности
углов СОА и СОВ, если полупрямая ОС лежит внутри L АОВ; и дополняет
эту полуразность до двух прямых углов, если полупрямая ОС лежит внутри
угла АОВ’, вертикального к углу АОВ. Он равен полусумме углов СОА
и СОВ, если эта полупрямая расположена внутри одного из двух других
углов ВО А’ или АОВ’, образованных данными прямыми (доказать).
3. Из точки О выходят четыре полупрямые О А, ОВ, ОС, OD (следующие
одна за другой в том порядке, как они перечислены), причём Z АОВ =
= /. COD и Z ВОС = Z DO А) доказать, что О А и ОС суть продолжения
одна другой и точно так же ОВ и OD.
4. Если четыре последовательные полупрямые О А, ОВ, ОС, OD таковы,
что биссектрисы углов АОВ и COD и точно так же биссектрисы углов ВОС
и AOD образуют одну прямую, то четыре полупрямые представляют попарно
продолжения одна другой (доказать).
*) Совершенно так же, как надпись, просвечивающая через лист, кажется
с обратной стороны листа перевёрнутой справа налево.

35 ПРЯМАЯ ЛИНИЯ УГЛЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

ПРЯМАЯ ЛИНИЯ УГЛЫ