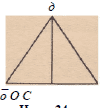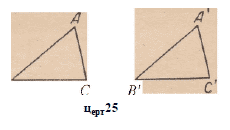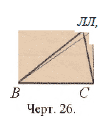ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ. КНИГА ПЕРВАЯ . ПРЯМАЯ ЛИНИЯ. ГЛАВА I I . ТРЕУГОЛЬНИКИ.

ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

 

ТРЕУГОЛЬНИКИ

Скачать всю книгу Ж. АДАМАР «ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ» в хорошем качестве
Ниже посмотрите текст для быстрого ознакомления(формулы отображаются не корректно):

21. Многоугольником называется часть плоскости, ограниченная
отрезками прямых линий (черт. 19). Эти последние образуют стороны
многоугольника. Их концы образуют вершины многоугольника.
Однако мы будем, вообще говоря, называть многоугольниками
только части плоскости, ограниченные одним контуром, который можно
описать одним росчерком пера. Таким образом, часть плоскости, которая
заштрихована на чертеже 2 1 , не будет являться для нас многоугольником.
Многоугольник называется выпуклым, если ни одна из
прямых, полученных неограниченным продолжением каждой его стороны,
не пересекает многоугольника. В противном случае (черт. 20)
он называется вогнутым.
Многоугольники классифицируют по числу сторон. Простейшими
многоугольниками будут: многоугольник с тремя сторонами, или
треугольник, многоугольник с четырьмя сторонами, или четырёхугольник,

многоугольник с пятью сторонами, или пятиугольник,
многоугольник с шестью сторонами, или шестиугольник. Мы будем
ещё рассматривать многоугольники с 8, 10, 12, 15 сторонами, называемые
соответственно восьмиугольником, десятиугольником, двенадцатиугольником,
пятнадцатиугольником.
Диагональю многоугольника называется отрезок, соединяющий
две непоследовательные вершины многоугольника.
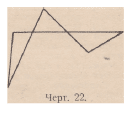
Пр и м е ч а н и е . Иногда, с несколько более общей точки зрения, называют
многоугольником любую замкнутую ломаную линию, стороны которой
могут пересекаться между собой (как на черт. 22). В этом последнем
случае, когда ломаная линия не ограничивает единственной площади, можно
назвать эту ломаную несобственным многоугольником. Наоборот, мы скажем,
что имеется многоугольник в собственном смысле, если мы хотим
указать, что мы имеем случай, изображённый на чертежах 19 или 20, а не
случай, изображённый на чертеже 22.

36 ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

22. Среди треугольников в частности различают:
Равнобедренный треугольник. Так называется треугольник с двумя
равными сторонами. Вершину, общую этим двум сторонам, называют
просто вершиной треугольника, а сторону, расположенную
против неё, — основанием.
Равносторонний треугольник, или треугольник с тремя равными
сторонами.
Прямоугольный треугольник, или треугольник с одним прямым
углом. Сторона, лежащая против прямого угла, называется гипотенузой;
стороны, образующие прямой угол, —
катетами *).
22а. Высотой треугольника называется
перпендикуляр, опущенный из вершины на
противоположную сторону; медианой называется
отрезок, соединяющий вершину с серединой
противоположной стороны.
23. Теорема. Во всяком равнобедренном
треугольнике углы, лежащие против
равных сторон, равны между собой.
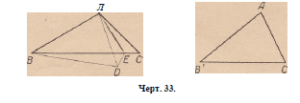
Пусть треугольник ABC — равнобедренный (черт. 23). Перевернём
угол ВАС и наложим его на самого себя (п. 1 0 ) так, чтобы сторона
АВ пошла по АС, и обратно.
Так как АВ и АС равны, точка В займёт положение точки С,
и наоборот. Следовательно, угол ABC совместится с углом АСВ, так
Д что эти два угларавны.
Обратная теорема. Если в треугольнике
два угла равны, то треугольник равнобедренный.
Пусть ABC—треугольник, в котором В= Z.C.
Перевернём этот треугольник так, чтобы сторона ВС
наложилась на самоё себя (п. 5), точка В перешла в
точку С, и обратно. Так как угол ABC равен
углу АСВ, то сторона В А пойдёт по СЛ, и обратно:
С А — по В А. Точка А, как точка пересечения
В А и С А, сохранит своё прежнее положение, и сторона АВ займёт
положение АС.
Следствие. Равносторонний треугольник будет в то же время
и равноугольный (т. е. все его углы будут равны), и обратно.
Теорема. Во всяком равнобедренном треугольнике биссектриса
угла при вершине перпендикулярна к основанию и проходит через
его середину.
Пусть AD—Абиссектриса угла А в равнобедренном треугольнике
ABC (черт. 24).

Если перевернуть угол ВАС и наложить его на самого себя, то
эта биссектриса не изменит своего положения, и то же самое будет
х) Определение катетов добавлено при переводе: во французском языке
соответствующий термин не употребляется, и в оригинале каждый раз
говорится: „стороны, образующие прямой уголм. Прим. ред. перевода.

37 ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

иметь место для точки D, в которой биссектриса пересекает основание.
Так как DB будет совмещено с DC и угол ADB с углом ADC,
д то мы будем иметь DB — DC и £ ADB= £ ADC.
П р и м е ч а н и е . Во всяком треугольнике ЛВС
можно рассматривать четыре прямые:
1°. биссектрису угла А;
2°. высоту, выходящую из точки А;
_ 3°. медиану, выходящую из той же точки;
о О С 4°. перпендикуляр к стороне ВС в её середине.
Черт. 24. Вообще эти четыре прямые будут отличны друг от
друга (см. упражнение 17). Предыдущая теорема показывает,
что в равнобедренном треугольнике они все сливаются в одну
прямую, которая является осью симметрии треугольника (п. 19а).
Эта теорема может быть также сформулирована иначе, а именно:
высота равнобедренного треугольника является в то же время его биссектрисой
и медианой; или еще: медиана равнобедренного треугольника
является в то же время его высотой и биссектрисой; перпендикуляр
к основанию в его середине проходит через вершину треугольника и является
биссектрисой угла при вершине.

Следствие. В равнобедренном треугольнике высоты, выходящие из
концов основания, между собой равны; то же самое имеет место для
медиан, выходящих из тех же вершин, и для биссектрис углов при этих
точках, так как эти прямые попарно симметричны.
24. Следующие предложения, известные под названием признаков
равенства треугольников, дают необходимые и достаточные условия
для того, чтобы два треугольника
были равны.
Первый признак равенства. Два
треугольника равны, если они имеют
по равной стороне и прилежащие
к этим сторонам углы тогой В
другого треугольника соответ- церт 25
ственно равны друг другу.
Пусть даны два треугольника ABC и А!ВГСГ (черт. 25), в коА
торых ВС = ВГСГ; £В=1’ВГ; £ С=£С.

черт 25

Наложим угол В1 на равный ему угол В так, чтобы сторона В> А*
приняла направление В А, а сторона ВГСГ—направление ВС. Так как
ВГСГ — ВС, то точка С совпадёт с С, а так как угол С равен углу С>
то сторона С’Аг примет направление СА. Вследствие этого точка А\
как точка пересечения прямых В1 А1 и С’А\ обязательно попадёт
в точку пересечения прямых В А и СА, т. е. в точку А. Совпадение
треугольников, таким образом, доказано.
Второй признак равенства. Два треугольника равны, если
они имеют по равному углу и заключающие эти углы стороны
того и другого треугольника соответственно равны друг
другу.
Пусть даны два треугольника ABC и АГВГС\ в которых / / А;
АВ = АГВ’\ АС= АГСГ (черт. 25).
Наложим угол А на равный ему угол А так, чтобы сторона А!В’
рриняла направление АВ п сторона АГСГ—направление АС. Так как

38 ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

ABf — АВ, то точка Вг попадёт в точку В; точно так же точка С
попадёт в С. ВГСГ совпадёт, таким образом, с ВСУ и совмещение
треугольников будет полное.
Третий признак равенства. Два треугольника равны, если они
имеют по три соответственно равные стороны.
Пусть даны два треугольника ABC и А!ВГС\ стороны которых
соответственно равны между собой. Расположим второй треугольник
таким образом, чтобы сторона В’СГ совпала с равной ей стороной ВС
и оба треугольника лежали по одну и ту же сторону от ВС. Пусть
ВСАХ — новое положение треугольника ВГСГА\ Я утверждаю, что
точка Ах совпадёт с точкой А. Это было бы оче- Л Л,
видно, если бы прямая ВА! приняла направление В А
или прямая С А! приняла направление СА. Если же
это было бы не так, то мы имели бы два равнобедренных
треугольника ВААХ и СААг (черт. 26),

и перпендикуляр
к отрезку AAt в его середине должен
был бы пройти через точки В и С (п. 23, мелкий
шрифт), иначе говоря, совместиться с прямой ВС. Это невозможно,
так как точки А и Ах лежат по одну сторону от ВС, и
потому ВС не может пройти через середину отрезка ААХ. Точки
А и Аг не могут быть, таким образом, различными, и два треугольника
совпадают между собой.
П р и м е ч а н и я . I. Для того чтобы доказать, что точка Ах совпадёт
с точкой А, мы смотрим, что произошло бы, если бы эти две
точки были различны; и приходя в этом случае к явно ошибочному заключению,
мы утверждаем, что этого быть не может.
Этот метод рассуждения называется доказательством от противного
и часто применяется при доказательствах.
II. В треугольнике имеется шесть главных элементов: три
угла и три стороны. Мы видим, что достаточно установить равенство
трёх из этих элементов (выбранных надлежащим образом)
в двух треугольниках, чтобы иметь возможность утверждать, что

треугольники равны, и в частности, что равны три остальных элемента.
III. Два равные треугольника (или вообще два многоугольника)
могут отличаться друг от друга направлением вращения (п. 2 0 ).
В этом случае они могут быть наложены друг на друга только с помощью
движения, выводящего один из них из плоскости. Напротив,
если направление вращения одинаково, то два многоугольника могут
быть приведены к совмещению простым скольжением в плоскости,
как мы эго увидим дальше.
25. Внешним углом выпуклого многоугольника называется угол,
образованный одной стороной и продолжением следующей стороны.
Теорема. Всякий внешний угол треугольника больше каждого
из внутренних углов, к нему не прилежащих.
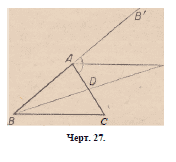
Пусть имеется треугольник ABC, в котором построен внешний
угол В1 АС (черт. 27).

39 ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

Я утверждаю, что этот угол больше, например, внутреннего угла С.
Чтобы это доказать, я провожу медиану BD, которую продолжаю на
длину DE, равную ей самой. Точка Е находится внутри угла В1 АС,
который будет больше угла ЕАС.

А этот последний равен углу С,
так как два треугольника DAE
и DCB равны как имеющие по
равному углу, заключённому между
соответственно равными сторонами.
Действительно, углы при
точке D равны как вертикальные;
AD=DC и BD = DE по построению.
Следовательно, внешний
угол В1 АС больше внутреннего
угла С, что и требовалось доказать.
Внешний угол ВАС будет
пополнительным для внутреннего
угла А. Угол С, будучи меньше угла ВГАС, в сумме с углом А даёт
величину, меньшую двух прямых. Наша теорема может быть сформулирована
так: сумма двух углов треугольника меньше двух
прямых. В частности треугольник не может

иметь более одного прямого или тупого угла.
Теорема. Во всяком треугольнике против
большей стороны лежит и больший угол.
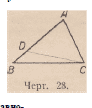
Пусть в треугольнике ABC (черт. 28) А/Г> АС.
Мы докажем, что А СА> Z. В. Для этого мы отложим
на АВ отрезок AD = AC. По предположению
отрезок DC расположен внутри первоначального
угла С, а следовательно, угол ACD меньше угла С. Но в равнобедренном
треугольнике ACD угол ACD равен углу ADC, который
больше угла В, как это следует из предыдущей теоремы, применённой
к треугольнику DCB. Теорема, таким образом, доказана.
Обратно, большему углу соответствует1) и большая сторона.
Это положение, очевидно, равносильно предыдущему.
26. Теорема. Во всяком треугольнике любая сторона меньше
суммы двух других сторон.
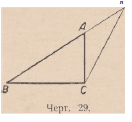
В треугольнике ABC продолжим АВ на длину AD = АС (черт. 29).

Требуется доказать, что BC<ABD*).
Проведя CD, мы видим, что угол D равен углу ACD (п. 23) и,
следовательно, меньше угла BCD.
Искомое неравенство вытекает, таким образом, из предыдущей
теоремы, применённой к треугольнику BCD.
*) Стороной, соответствующей данному углу треугольника, называется
сторона, ему противолежащая.
2) Теорема очевидна, если ВС — не самая большая из’ сторон треугольника.

40  ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

Следствия: I. Во всяком треугольнике любая сторона больше
разности двух других.
Действительно, неравенство ВС<ААВ -|- АС даёт после вычитания
АС из обеих частей:
ВС—АС<СЛВ.

II. Каковы бы ни были три точки А, В, С, каждое из расстояний
ВС, С А, АВ равняется самое боль- п
шее сумме двух других и самое меньшее
их разности, причём равенство может
иметь место только, если три точки
расположены на одной прямой.
Теорема. Прямолинейный отрезок
короче всякой ломаной линии, имеющей
с ним общие концы.

Если ломаная линия составлена из
двух отрезков, то теорема сводится к
предыдущей.
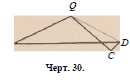
Пусть теперь ломаная линия ABCD состоит из трёх отрезков
(черт. 30). Соединив В с D, получим
AD<AAB-\-BD,
и так как BD ВС -f- CD, то
AD < АВ -|- BD < АВ -f- ВС -f- CD.
Теорема, таким образом, доказана для линии, состоящей из трёх
отрезков; совершенно так же убедимся последовательно в справедли-
Q вости теоремы для ломаных линий, составленных
из 4, 5 и т. д. отрезков. Теорема

ТРЕУГОЛЬНИКИ. Многоугольник.

оказывается справедливой при всяком
D числе отрезков, образующих ломаную
С линию.
Черт. 30. *14.Периметром многоугольника или ломаной
линии называется сумма всех сторон.
Теорема. Периметр выпуклой ломаной меньше периметра
любой ломаной, объемлющей данную и имеющей с ней общие
концы.
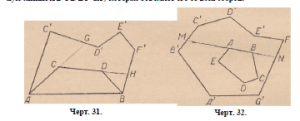
Пусть ACDB — выпуклая ломаная линия и ACrDEFB — объемлющая
её ломаная (черт 31). Продолжим стороны АС и CD в одном
и том же направлении ACDB, т. е. сторону АС за точку С, а сторону
CD — за точку D. Эти продолжения пересекут объемлющую
линию соответственно в точках О и И.
Путь ACDB короче пути АСИВ, так как они имеют общую часть
ACD, а остающаяся часть DB первого короче остающейся части DHB
второго. В свою очередь, путь АСНВ меньше, чем AGD’EFB, так

41 ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

как, отбрасывая общие части ЛС, НВ, получим отрезок СИ, который
короче ломаной линии CGD’E’FH.
Наконец, точно так же AGDEFB меньше ACD’E’F’B, так как
АО меньше ACG.
Таким образом, имеем:
ACDB < АСНВ < AGD’E’F’B < ACD’E’F’B.
Следствие. Периметр выпуклого многоугольника меньше периметра
замкнутой ломаной линии, которая объемлет его со всех
сторон.
Пусть (черт. 32) имеем выпуклый многоугольник ABCDE и ломаную
линию A’B’C’D’E’F’GA’, которая объемлет его со всех сторон.
Черт. 31. Черт. 32.

Продолжим сторону АВ в обоих направлениях до пересечения с объемлющей
линией в точках М> N; мы видим, что линия AEDCB меньше
AMBA’G’NB (по предыдущей теореме), так что многоугольник
AEDCBA имеет периметр меньший, чем многоугольник NMBA’G’N.
Л
Черт. 33.
А этот в свою очередь по длине меньше данной объемлющей линии,
так как часть MBAGNу них общая, a MN < A M C f D f E f F f N .
28. Теорема. Если два треугольника имеют по неравному
углу, заключённому между соответственно равными сторонами,
то третьи стороны неравны и против большего угла лежит
и большая сторона.

Пусть даны треугольники ABC и А’В’Св которых АВ — А’В\
АС = АС, Л А А’ (черт. 33). Я хочу доказать, что ВС больше
ВС’.

42 ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

Наложим треугольник А’ВГСТ на треугольник ABC так, чтобы две
равные их стороны АГВГ и АВ совпали. Так как угол А’ меньше угла А,
то сторона А’С’ займёт положение AD внутри угла ВАС. Проведём
биссектрису АЕ угла DAC; эта прямая точно так же лежит внутри
угла ВАС. Следовательно, точки В и С лежат по разные стороны
от неё, и прямая АЕ должна пересечь сторону ВС в некоторой точке Е,
расположенной между В и С. Если мы проведём DE, то увидим, что
два треугольника АСЕ и ADE равны как имеющие по равному углу
(углы при Л), заключённому между двумя соответственно равными
сторонами (АЕ общая, AC—A’C’—AD)\ отсюда следует равенство
сторон DE и ЕС. Далее неравенство BD < л В Е E D , вытекающее из
треугольника BDE, даёт нам
BD < BE -f ЕС или BD < ВС.
Обратная теорема. Если две стороны одного треугольника
соответственно равны двум сторонам другого, а третьи стороны
неравны между собой, то углы, противолежащие этим сторонам,

также неравны и против большей стороны лежит и больший угол.
Это положение равносильно предыдущему.
П р и м е ч а н и е . Предыдущая теорема ни в какой мере не предполагает
доказанным третий признак равенства треугольников (п. 24). Наоборот,
она даёт для него новое доказательство.
Если, в самом деле, одновременно с АВ = А’В’ и АС = А’С’ имеем
ВС = В’С\ то необходимо, чтобы углы при точках А, А’ в двух треугольниках
были равны, так как иначе стороны ВС и В’С’ были бы неравны
между собой, как мы только что видели. Но если Z. А = L А\ то два
треугольника равны (второй признак равенства).
УПРАЖНЕНИЯ.
5. Доказать, что треугольник равнобедренный:
1°. если его биссектриса является в то же время и высотой;
2°. если его медиана является в то же время и высотой;
3°. если его биссектриса является в то же время и медианой.
6. На стороне ОХ некоторого угла отложены два отрезка О А и ОВ,

а на другой стороне угла ОХ’ два отрезка OA1, OB’, соответственно равные
первым, и концы отрезков накрест соединены между собой: А с В’,
г. А’ с В. Доказать, что точка /, в которой пересекаются прямые АВ’
и А’В, лежит на биссектрисе данного угла.
7. Если две стороны треугольника неравны между собой, то медиана,
заключённая между ними, образует с меньшей из этих сторон угол больший,
чем с другой стороной (доказать, пользуясь построением, аналогичным
построению п. 25).
8. Если соединить точку, взятую в плоскости треугольника, с тремя
вершинами, то сумма полученных отрезков больше полупериметра треугольника;
если точка взята внутри треугольника, то она меньше его периметра
(доказать).
8а. Если соединить точку, взятую в плоскости многоугольника, со
всеми его вершинами, то сумма полученных отрезков больше полупериметра
многоугольника (доказать).
9. Сумма диагоналей выпуклого четырёхугольника заключается между
его полупериметром и периметром (доказать).

43 ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

10. Точка пересечения диагоналей выпуклого четырёхугольника есть
точка плоскости, которая имеет наименьшую возможную сумму расстояний
до его четырёх вершин (доказать).
11. Медиана треугольника меньше полусуммы сторон, её заключающих,
и больше разности между этой полусуммой и половиной третьей стороны
(доказать).
12. Сумма медиан треугольника больше полупериметра и меньше периметра
(доказать).
13. Найти на данной прямой точку, сумма расстояний которой до двух
заданных точек наименьшая. Рассмотреть два случая: когда обе точки
находятся по одну и ту же или по разные стороны от прямой.
Свести первый случай ко второму (пользуясь симметрией части фигуры
относительно данной прямой).
14. (Задача о биллиарде.) Даны прямая XY и две точки А, В по одну
и ту же сторону от этой прямой; найти на этой прямой точку М такую,
чтобы угол АМХ был бы равен углу BMY.

Получается та же точка, что и в предыдущем упражнении.
15. Найти на данной прямой такую точку, чтобы разность расстояний
её от двух заданных точек была наибольшей. Рассмотреть два случая,
когда обе точки находятся по одну и ту же или по разные стороны от
прямой.

44 ТРЕУГОЛЬНИКИ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

ТРЕУГОЛЬНИКИ