Теорема Шаля

Теорема Шаля.

Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):

Скачать бесплатно: Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ ПЛОСКОСТИ И ЕЕ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. З. А. Скопец, Л. И. Кузнецова

(стр. 227-246)

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.

§ 7. Теорема Шаля.  А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.

В предыдущих параграфах было доказано существование осевых
симметрий и поворотов. Другой вид перемещений — параллельный
перенос — определяется в учебном пособии (п. 36). В главе III пособия
доказывается, что параллельный перенос является перемещением.
Но так как при этом принимается без доказательства транзитивность
отношения сонаправленности лучей, это доказательство
естественно провести в настоящей работе. При доказательстве мы
будем опираться на аксиому параллельных и некоторые ее следствия,
полученные в главе III учебного пособия;
Напомним сначала определения.
Пусть лучи ОхА и 02В лежат на параллельных прямых а и b
соответственно. В случае, когда эти прямые совпадают, лучи 0,Л
и 02В называют одинаково направленными (короче — сонаправлен-
ными), если один из них содержит другой; в противном случае
эти лучи называются противоположно направленными. В случае,
когда прямые а и b различны, лучи ОхЛ и 02В называют сонаправ-
ленными, если они лежат в одной полуплоскости с границей 0Х02,
и противоположно направленными, если эти лучи лежат в различных
полуплоскостях с границей 0Х02. Сонаправленность лучей
обозначают значком ff, а противоположную направленность — fj.
Рассмотрим произвольные пересекающиеся прямые а и Ь
(рис. 25). Параллельным проектированием плоскости на прямую а
параллельно прямой b называется следующее отображение.
Пусть X — произвольная точка плоскости. Существует единственная
прямая с, проходящая через X и параллельная Ь. Прямая а,
пересекающая одну из параллельных прямых b и с, пересекает с
в некоторой точке Y. По определению Y — образ точки X при проектировании
на прямую а параллельно прямой b; это проектирование
обозначается Рь
а или просто Р.
У.7.1. Если прямые г и q параллельны, то образом луча г’ с на-
чалом О при проектировании Р на прямую q параллельно b является
луч с началом Р (О), сонаправленный с г’.
Д о к а з а т е л ь с т в о . Если прямые г и q совпадают, справедливость
У.7.1 очевидна. Пусть эти прямые различны. Обозначим
через а прямую, параллельную Ь и проходящую через О; аа~*
полуплоскость с границей а, содержащая г’ (рис. 26).

273 Теорема Шаля. 

По определению проектирования прямые а и q не параллельны.
Значит, открытые лучи прямой q с началом Р (О) целиком содержатся
в открытых полуплоскостях с границей а. Пусть q’ — открытый
луч с началом Р (О), лежащий в полуплоскости а’а. Прямая,
параллельная а и проходящая через произвольную точку М открытого
луча г’, не пересекается с а и, следовательно, содержится
в а’а. Поэтому образ г’ при проектировании Р — подмножество
луча q’. Остается заметить, что каждая точка К луча q’ является
образом некоторой точки N луча г’ (N — точка пересечения г’
с прямой, параллельной b и проходящей через К).
У.7.2. Пусть прямые а, Ь и с принадлежат одному пучку параллельных.
Если лучи а’ и Ь’ одинаково (противоположно) направлены,
то и образы этих лучей при параллельном проектировании на прямую
с одинаково (противоположно) направлены.
Д о к а з а т е л ь с т в о . Если лучи ak и Ь’с содержатся в одной
прямой, справедливость У.7.2 очевидна. Пусть аФ Ь. Образы лучей
а[ и Ьс при проектировании Pd
c можно получить так: спроектировать
a’k и b’c параллельно d на Ь, а затем спроектировать b на с
параллельно d (рис. 27). Обозначим проектирование на Ь через Р.
В силу У.7.1 образ луча ak при проектировании Р — луч прямой
Ь, сонаправленный с %. Обозначим этот луч через b’D (D —
образ точки К при проектировании Р). Точки луча b’c при проектировании
Р остаются на месте. Докажем, что bc ff bo.
Допустим, что это не так. Тогда be fj bo. Введем на прямой Ь
систему координат с началом С так, что координаты луча Ьс —
неотрицательные числа. Мы предположили, что лучи Ьс и Ьо противоположно
направлены. Значит, существует такое число t0, что луч
b’D состоит из точек, координаты которых не больше t0.
Выберем точку М луча b’D с отрицательной координатой, меньшей
/0. Существует точка N луча ak, такая, что Р (N) — М. Так
как a’k ff be, открытые лучи а* и Ьс лежат в одной полуплоскости
с границей КС. Точка М не
принадлежит открытому лучу
Ь’г, и, следовательно, М и а! ле- /V а жат в различных открытых по-
луплоскостях с границей КС.
Значит, ШМ П (КС) ф 0.
Из теоремы Паша следует,
что прямая MN пересекает и отрезок
KD. Это невозможно: по
определению проектирования
(MN) || (KD).
Следовательно, лучи Р (а’к)
и Ь^ сонаправлены. При про-

274 Теорема Шаля. 

ектировании на прямую с отношение сонаправленности сохраняется.
Доказательство сохранения отношения противоположной направленности
теперь очевидно.
Прежде чем перейти к доказательству теоремы о транзитивности
отношения сонаправленности лучей, докажем ее для одного частного
случая.
У.7.3. Если лучи а а, Ь’в, с’с содержатся в прямой р и a a ft Ьв,
Ьв ft с’с, то а’А ft с’с.
Д о к а з а т е л ь с т в о . Введем на р такую систему координат
с началом в точке В, что координаты точек луча Ъ’ь — неотрицательные
числа. Пусть ха и хс— координаты точек Л и С. Так как лучи
ал и Ьв, Ь’в и с’с сонаправлены, имеем:
аА = {М: хм > ха }, с’с —; {N: xn > хс }.
Очевидно, что если ха ^ хс, то а’А с: с’с. Если же ха < хс, то
а’л гэ сс. Следовательно, ал ft с’с.
Т е о р е м а 7.1 (о транзитивности отношения сонаправленности
лучей). Если a’ ff Ь’ и b’ ff с’, то а’ ff с’.
Д о к а з а т е л ь с т в о . — Из определения. сонаправленных лучей
сразу получаем, что а, b и с — прямые одного пучка параллельных.
Проектированием Р ца прямую Ь переведем лучи а!г Ь’ и с’
в прямую Ь. По У.7.2 Р (a’) ff Р (&’), Р {Ь’) ff Р (с’).
Вследствие У.7.3 луч Р (а’) сонаправлен лучу Р (с’). Отсюда
следует, что и a’ ff с’.
В самом деле, пусть это не так. Поскольку а || с, отсюда получаем,
что а’ с’. Но тогда вследствие У.7.2 и лучи Р (а’), Р (с’)
противоположно направлены. Противоречие.
Для удобства чтения сформулируем следующие утверждения,
доказанные в учебном пособии (см. п. 36).
Т е о р е м а 7.1. Параллельный перенос является перемещением.
Т е о р е м а 7.3. Для того чтобы перемещение являлось параллельным
переносом, необходимо и достаточно, чтобы оно каждый
луч плоскости отображало на сонаправленный ему луч.
У.7.4. Центральная симметрия отображает каждый луч плоскости
на противоположно направленный ему луч.
Очевидное следствие последних двух предложений — такое утверждение.
У .7.5. Композиция двух центральных симметрий — параллельный
перенос:
ZotoZol = 20102, . (1)
ZoloZo, = 26fi1. (2)
Д о к а з а т е л ь с т в о . Как это следует из У.7.4, произвольный
луч плоскости при композиции двух центральных симметрий
отображается на сонаправленный ему луч. По теореме 7.3 эта композиция
— перенос.
Для доказательства (1) и (2) остается вспомнить, что перенос

275 Теорема Шаля. 

вполне определяется указанием произвольной
точки плоскости и ее образа, и найти
образы точек Ох и 02 при композициях
Zo1 0 Zo2 и Zo, ° Zo2.
Т е о р е м а 7.4. Если оси симметрий
Sa и Sb параллельны, то композиция этих
симметрий — перенос.
Д о к а з а т е л ь с т в о . 1) Если а—
Рис. 28 — Ь, то Sa° S„ = Е. По определению
тождественное отображение Е плоскости
есть перенос.
2) Пусть аф Ь (рис. 28). Проведем прямую с, перпендикулярную
а. Тогда с X Ь. Пусть Ог = с Л а» Ог = с [\ Ъ. Вследствие
теорем § 5 Sa° Sc = Z0l, Sc ° Sb = Z0„ Sa о Sb = Sa° E q Sb =
= Sa о (Sc с Se) о Sb = (Sa о Sc) » (Se о Sb) = Zo^o Z0i = 20A.
Аналогично доказывается, что Sb ° Sa — 20i02.
В § 5 было показано, что композиция поворотов с общим центром
есть поворот. Докажем более общую теорему.
Т е о р е м а 7.5. Композиция двух поворотов есть поворот или
перенос.
Д о к а з а т е л ь с т в о . Повороты R0l и Ro, можно представить
в виде Rot = Sx ° Sa, Ro„ = Sa ° Sy, где а: и у — прямые,
проходящие через точки Ог и 02 соответственно, и а — (О^).
Тогда Ro, о /?0j = (S* о Se) о (Sa о Sy) = Sx ° Sl ° Sy = Sx° Sy.
Если x || у, то Ro, ° Ro2 — перенос (теорема 7.4); если прямые
хну пересекаются, Ro, ° Ro, — поворот.
Т е о р е м а 7.6. Композиция нетождественного поворота R%
и переноса Т — поворот.
Д о к а з а т е л ь с т в о . В случае Т — Е результат очевиден.
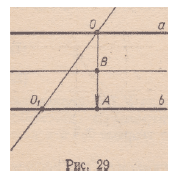
Пусть Т Ф Е и А = Т (О) (рис. 29).

По теореме 7.4 Т = Sa о Sb, где а и b — такие прямые, что
а проходит через О и Ь || а. По теореме 5.2 существует прямая
с, проходящая через О и такая, что Sc о Sa = R0. Тогда
Ro о Т = (Sc о SJ о (Sa о Sb) = S£ о Sb.
По условию R ф Е. Значит, с Ф а и прямые b и с пересекаются
в некоторой точке Ох. Вследствие теоремы
5.1 Sc о Sb— поворот с центром Ох.
Аналогично доказывается, что Т ° R — поворот.
В общем случае Т ° R Ф R ° Т
(докажите). Угол поворота Ro° Т легко определить;
при переносе Т каждый луч а’
переходит в сонаправленный ему луч Ь’, а
угол между направлениями, задаваемыми
лучами Ь’ и R (&’), равен ср. Следовательно,
композиция переноса и поворота
поворот на угол ф.

276 Теорема Шаля. 

Определим новый вид перемещений: скользящей симметрией
называется композиция симметрии Sa и переноса АВ, где (АВ) ||а.
(Заметим, что Sa ° АВ = АВ о Sa.)
Т е о р е м а 7.7. Композиция переноса 7\ и скользящей симметрии
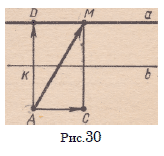
Sao Т — скользящая симметрия.
Д о к а з а т е л ь с т в о . Если направление переноса Тх =
= AM параллельно оси симметрии а, то результат очевиден. Пусть
это не так (рис. 30). Представим AM в виде композиции переносов
АС и AD, таких, что (AD) _L а, (АС) || а:
AM = AC+ AD.
Вследствие коммутативности сложения векторов (см. «Геометрия,
6—8» п. 57.)
Sa о Т о Тг = (Sa о AD) о (АС о Т).
На прямой DA возьмем точку К, удаленную от а на расстояние
Y \AD\. Рассмотрим прямую Ь, такую, что b || a, K £ b .
Точки прямой b — неподвижные точки Sa о AD. Так как Sa о
о AD Ф Е, то Sa о AD = Sb. Значит, (Sa о Т)° Ti — (Sb ° АС) ° Т,
причем направление АС ° Т параллельно а. В силу замечания,
сделанного в начале доказательства, (5а ° Т) о Тг — скользящая
симметрия.
Т е о р е м а 7.8 (Шаля). Всякое перемещение плоскости является
либо поворотом, либо параллельным переносом, либо скользящей
симметрией.
Д о к а з а т е л ь с т в о . Пусть F — произвольное перемещение
плоскости. По теореме 2.3 F имеет либо одну неподвижную точку
(в этом случае F — поворот), либо прямую из неподвижных точек
(в этом случае F — осевая симметрия), а по определению симметрии
являются скользящими симметриями, либо F является
тождественным отображением плоскости (т. е. и поворотом, и переносом
одновременно), либо F не имеет неподвижных точек. Осталось
рассмотреть этот последний случай.
Возьмем произвольную точку А. По предположению В —
— F (А) Ф А. Обозначим через Т перенос,
переводящий В в А, и рассмотрим перемещение
Т о F = Ft. Точка А — неподвижная
точка этого перемещения. Возможны
три случая.
1) FX = E.
Тогда Е = Т о F. Отсюда F = Т \
так как Г-1 — перенос (см. «Геометрию,
6—8», п. 55), то F — перенос.
2) Fx — осевая симметрия.

277 Теорема Шаля. 

Тогда F = Т 1 о S. По теореме 7.7 F — скользящая симметрия.
3) Fx —• поворот R.
Тогда F = Т~х о Но Г”1 — перенос. По теореме 7.6 F —
поворот.
Теорема Шаля доказана.
ЛИТЕРАТУРА
1. А б р а м о в А. М. Логические основы курса геометрии восьмилетней
школы. Пособие для учителя. НИИ школ МП РСФСР. М., 1974.
2. А б р а м о в А. М. Логические основы курса планиметрии. — Математика
в школе, 1974, № 5, с. 51—62.
3. Б у з е м а н П . , К е л л и Д. Проективная геометрия и проективные
метрики. М., ИИЛ, 1962.
4. Г и н д и к и н С. А. Измерение углов. — Математика в школе, 1974,
No 6.
5. К а л у ж н и н Л. А. Элементы теории множеств и математической логики
в школьном курсе математики. Пособие для учителей. М., Просвещение,
1978.
6. Р о б е р т Р . С т о л л . » Множества. Логика. Аксиоматические теории.
М., Просвещение, 1968.
7. А. Д о н е д д ю. Евклидова планиметрия. М., Наука, 1979.

278 Теорема Шаля. 

На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика.  Математика в школе.

Теорема Шаля