Глава I. ПЯТОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ. Разнообразие погоды.
ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман ИЗДАНИЕ ДВЕНАДЦАТОЕ СТЕРЕОТИПНОЕ
Под редакцией и с дополнениями В. Г. Болтянского
Скачать 11-ое издание ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман в формате PDF в хорошем качестве, но без возможности каптирования на Главной странице ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Текст для быстрого ознакомления (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):
Разнообразие погоды
ЗАДАЧА
Будем характеризовать погоду только по одному
признаку, — покрыто ли небо облаками или нет, т. е.
станем различать лишь дни ясные и пасмурные. Как
вы думаете, много ли при таком условии возможно
недель с различным чередованием погоды?
Казалось бы, немного: пройдет месяца два, и все
комбинации ясных и пасмурных дней в неделе будут
исчерпаны; тогда неизбежно повторится одна из тех
комбинаций, которые уже наблюдались прежде.
Попробуем, однако, точно подсчитать, сколько различных
комбинаций возможно при таких условиях.
Это — одна из задач, неожиданно приводящих к пятому
математическому действию.
Итак: сколькими различными способами могут на
одной неделе чередоваться ясные и пасмурные дни?
РЕШЕНИЕ
Первый день недели может быть либо ясный, либо
пасмурный; имеем, значит, пока две «комбинации».
В течение двухдневного периода возможны следующие
чередования ясных и пасмурных дней:
ясный и ясный
ясный и пасмурный
пасмурный и ясный
пасмурный и пасмурный.
Итого в течение двух дней 22 различного рода чередований.
В трехдневный промежуток каждая из
четырех комбинаций первых двух дней сочетается с
двумя комбинациями третьего дня; всех родов чередований
будет
За пять дней возможно 25, за шесть дней 26 и, наконец,
за неделю 27= 128 различного рода чередований.
стр. 12 Разнообразие погоды.
Отсюда следует, что недель с различным поряд-
ком следования ясных и пасмурных дней имеется 128.
Спустя 128*7=896 дней необходимо должно повториться
одно из прежде бывших сочетаний; повторение,
конечно, может случиться и раньше, но 896 дней —
срок, по истечении которого такое повторение неизбежно.
И обратно: может пройти целых два года, даже
больше (2 года и 166 дней), в течение которых ни
одна неделя по погоде не будет похожа на другую.
стр. 13 Разнообразие погоды.
На главную страницу ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман.
Школьная математика. Математика в школе.

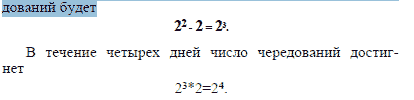


Comments