ГЛАВА VIII ПРОГРЕССИИ. Древнейшая прогрессия.
Сборник МатематикиГЛАВА VIII ПРОГРЕССИИ.ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман ИЗДАНИЕ ДВЕНАДЦАТОЕ СТЕРЕОТИПНОЕ. Под редакцией и с дополнениями В. Г. Болтянского Скачать 11-ое издание ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман в формате PDF в хорошем качестве, но без возможности капирования на Главной странице ЗАНИМАТЕЛЬНАЯ АЛГЕБРА Я. И. Перельман. |
Текст просто для быстрого ознакомления с темой в общих чертах (формулы и чертежи могут отображаться не точно). Качественнее отображаются в PDF файле выше):
Древнейшая прогрессия
ЗАДАЧА
Древнейшая задача на прогрессии — не вопрос о
вознаграждении изобретателя шахмат, насчитываю-
щий за собой двухтысячелетнюю давность, а гораздо
более старая задача о делении хлеба, которая запи-
сана в знаменитом египетском папирусе Ринда. Папи-
рус этот, разысканный Риндом в конце прошлого
столетия, составлен около 2000 лет до нашей эры ц
является списком с другого, еще более древнего ма-
тематического сочинения, относящегося, быть может,
к третьему тысячелетию до нашей эры. В числе ариф-
метических, алгебраических и геометрических задач
этого документа имеется такая (приводим ее в воль-
ной передаче);
Сто мер хлеба разделить между пятью людьми
так, чтобы второй получил на столько же больше пер-
вого, на сколько третий получил больше второго, чет-
вертый больше третьего и пятый больше четвертого.
Кроме того, двое первых должны получить в 7 раз
меньше трех остальных. Сколько нужно дать каждому?
РЕШЕНИЕ
Очевидно, количества хлеба, полученные участни-
ками раздела, составляют возрастающую арифмети-
170 ПРОГРЕССИИ
ческую прогрессию. Пусть первый ее член х, раз*
ность у. Тогда
доля первого .V
» второго v~by
» третьего -* + 2у
» четвертого x-f-3y
» пятого х-\-Ау.
На основании условий задачи составляем следую*
щне два уравнения:
\7[х + (х + у)\ = (
После упрощений первое уравнение получает вид
а второе!
Решив эту систему, получаем:
Значит, хлеб должен быть разделен на следующие
части
Алгебра на клетчатой бумаге
Несмотря на пятидесятивековую древность этой
задачи на прогрессии, в нашем школьном обиходе
прогрессии появились сравнительно недавно. В учеб*
пике Магницкого, изданном двести лет назад и сл>-
жившем целых полвека основным руководством для
школьного обучения, прогрессии хотя и имеются, но
общих формул, связывающих входящие в них вели-
чины между собой, в нем не дано. Сам составитель
учебника не без затруднений справлялся поэтому
с такими задачами. Между тем формулу суммы чле*
нов арифметической прогрессии легко вывести про-
стым и наглядным приемом с помощью клетчатой
бумаги. На такой бумаге любая арифметическая
171 ПРОГРЕССИИ
прогрессия изображается ступенчатой фигурой. Напри-
мер, фигура ABDC на рис. 33 изображает Прогрессию:
2; 5; 8; 11; 14.
Чтобы определить сумму ее членов, дополним чер«
теж до прямоугольника ABGE. Получим две равные
фигуры ABDC и DGEC. Площадь каждой из них
изображает сумму членов нашей прогрессии. Значит,
двойная сумма прогрессии равна площади прямо-
угольника ABGE, т. е.
(АС + СЕ) -АВ.
Но АС + СЕ изображает сумму 1-го и 5-го членов
прогрессии; АВ — число членов прогрессии. Поэтому
двойная сумма
2S— (сумма крайних членов) • (число членов)
или
(первый -[- последний член) • (число членов)
Поливка огорода
ЗАДАЧА
В огороде 30 грядок, каждая длиной 16 м и ши-
риной 2,5 м. Поливая грядки, огородник приносит
ведра с водой из колодца, расположенного в 14 м от
172 Алгебра на клетчатой бумаге
края огорода (рис. 34)’, и обходит грядки по меже,
причем воды, приносимой за один раз, достаточно
для поливки только одной грядки.
Какой длины путь должен пройти огородник, по-
ливая весь огород? Путь начинается и кончается у
колодца.
РЕШЕНИЕ
Для поливки первой грядки огородник должен
пройти путь
14+16 + 2,5+16 + 2,5+14 = 65 ли
При поливке второй он проходит
14 + 2,5+16 + 2,5+16 + 2,5 + 2,5+14 = 65 + 5 = 70 м.
Каждая следующая грядка требует пути на 5 м длин-
нее предыдущей. Имеем прогрессию:
65; 70; 75; … ; 65 + 5-29.
Сумма ее членов равна
F5 + 65 + 23-5K0 =
Огородник при поливке всего огорода проходит
путь в 4,125 км.
173 Поливка огорода

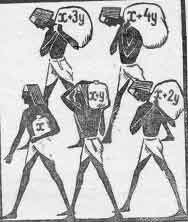


Comments